广东省深圳市2021年中考数学五模试卷

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列倡导节约的图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列几何体中，其三视图的三个视图完全相同的是（　　）

A、 B、 C、 D、

查看试题解析
3. 在数轴上，点A，B在原点O的两侧，分别表示数a和3，将点A向左平移1个单位长度，得到点C．若 $O C = O B$ ，则a的值为（）．

A、 $- 3$ B、 $- 2$ C、 $- 1$ D、2

查看试题解析
4. 一个多边形的每个内角均为120°，则这个多边形是（　　）

A、四边形 B、五边形 C、六边形 D、七边形

查看试题解析
5. 电影《流浪地球》中，人类计划带着地球一起逃到距地球4光年的半人马星座比邻星．已知光年是天文学中的距离单位，1光年大约是95000亿千米，则4光年约为（　　）

A、9.5×10⁴亿千米 B、95×10⁴亿千米 C、3.8×10⁵亿千米 D、3.8×10⁴亿千米

查看试题解析
6. 如果a﹣b＝ $\sqrt{3}$ ，那么代数式 $(\frac{b^{2}}{a} - a) \cdot \frac{a}{a + b}$ 的值为（　　）

A、﹣ $\sqrt{3}$ B、 $\sqrt{3}$ C、3 D、2 $\sqrt{3}$

查看试题解析
7. 已知 $⊙ O_{1}$ ， $⊙ O_{2}$ ， $⊙ O_{3}$ 是等圆， $△ A B P$ 内接于 $⊙ O_{1}$ ，点C ， E分别在 $⊙ O_{2}$ ， $⊙ O_{3}$ 上．如图，①以C为圆心， $A P$ 长为半径作弧交 $⊙ O_{2}$ 于点D ，连接 $C D$ ；②以E为圆心， $B P$ 长为半径作弧交 $⊙ O_{3}$ 于点F ，连接 $E F$ ；下面有四个结论：① $C D + E F = A B$ ；② $\overset{⌢}{C D} + \overset{⌢}{E F} = \overset{⌢}{A B}$ ；③ $∠ C O_{2} D + ∠ E O_{3} F = ∠ A O_{1} B$ ；④ $∠ C D O_{2} + ∠ E F O_{3} = ∠ P$ ，所有正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 改革开放40年以来，城乡居民生活水平持续快速提升，居民教育、文化和娱乐消费支出持续增长，已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出，如图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图．

说明：在统计学中，同比是指本期统计数据与上一年同期统计数据相比较，例如2018年第二季度与2017年第二季度相比较；环比是指本期统计数据与上期统计数据相比较，例如2018年第二季度与2018年第一季度相比较．

根据上述信息，下列结论中错误的是（　　）

A、2017年第二季度环比有所提高 B、2017年第三季度环比有所提高 C、2018年第一季度同比有所提高 D、2018年第四季度同比有所提高

查看试题解析
9. 已知点A(a－m ， y₁)、B(a－n ， y₂)、C(a+b ， y₃)都在二次函数y=x²－2ax +1的图象上，若0<m<b<n ，则y₁、y₂、y₃的大小关系是（）

A、y₁< y₂< y₃ B、y₁ < y₃< y₂ C、y₃< y₁< y₂ D、y₂< y₃< y₁

查看试题解析
10. 如图，一次函数 $y = x + 3$ 的图象与x轴，y轴交于A ， B两点，与反比例函数 $y = \frac{4}{x}$ 的图象相交于C ， D两点，分别过C ， D两点作y轴，x轴的垂线，垂足为E ， F ，连接 $C F ， D E$ ．有下列四个结论：① $△ C E F$ 与 $△ D E F$ 的面积相等；② $△ A O B ∽ △ F O E$ ；③ $△ D C E ≌ △ C D F$ ；④ $A C = B D$ ．其中正确的结论是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若代数式 $\frac{1}{x - 4}$ 有意义，则实数x的取值范围是.

查看试题解析
12. 如图，在△ABC中，AB=AC=5，BC=8，中线AD、CE相交于点F ，则AF的长为．

查看试题解析
13. 如图，已知正方形OABC的三个顶点坐标分别为A (2，0)，B (2，2)，C (0，2)，若反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象与正方形OABC的边有交点，请写出一个符合条件的k值．

查看试题解析
14. 如图，四边形 $A B C D$ 是平行四边形， $⊙ O$ 经过点A ， C ， D与 $B C$ 交于点E ，连接 $A E$ ，若 $∠ D = 72 °$ ，则 $∠ B A E =$ ．

查看试题解析
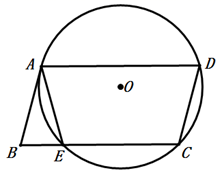15. 如图所示的网格是正方形网格，则 $∠ B A C - ∠ D A E =$ °（点A，B，C，D，E是网格线交点）．

查看试题解析

三、解答题

16. 计算： ${(\frac{1}{2})}^{- 2} - {(π - \sqrt{7})}^{0} + | \sqrt{3} - 2 | + 4 s i n 60 °$ ．

查看试题解析
17. 化简： $\frac{2 a - 1}{a - 1} + \frac{a^{2} - 1}{a} \div \frac{a^{2} - 2 a + 1}{a}$ ，并挑选合适的值代入求值．

查看试题解析
18. 某校在宣传“民族团结”活动中，采用四种宣传形式：A．器乐，B．舞蹈，C．朗诵，D．唱歌．每名学生从中选择并且只能选择一种最喜欢的，学校就宣传形式对学生进行了抽样调查，并将调查结果绘制了如下两幅不完整的统计图．

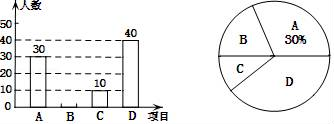
请结合图中所给信息，解答下列问题：

(1)、本次调查的学生共有人；

(2)、补全条形统计图；

(3)、该校共有1200名学生，请估计选择“唱歌”的学生有多少人？

(4)、七年一班在最喜欢“器乐”的学生中，有甲、乙、丙、丁四位同学表现优秀，现从这四位同学中随机选出两名同学参加学校的器乐队，请用列表或画树状图法求被选取的两人恰好是甲和乙的概率．

查看试题解析
19. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D是 $B C$ 边的中点，连接 $A D$ ，分别过点A，C作 $A E ∥ B C$ ， $C E ∥ A D$ 交于点E，连接 $D E$ ，交 $A C$ 于点O．

(1)、求证：四边形 $A D C E$ 是矩形；

(2)、若 $A B = 10$ ， $\sin ∠ C O E = \frac{4}{5}$ ，求 $C E$ 的长．

查看试题解析
20. 某大型企业为了保护环境，准备购买A、B两种型号的污水处理设备共8台，用于同时治理不同成分的污水，若购买A型2台、B型3台需54万，购买A型4台、B型2台需68万元．

(1)、求出A型、B型污水处理设备的单价；

(2)、经核实，一台A型设备一个月可处理污水220吨，一台B型设备一个月可处理污水190吨，如果该企业每月的污水处理量不低于1565吨，请你为该企业设计一种最省钱的购买方案．

查看试题解析
21. 如图1，点E为△ABC边AB上的一点，⊙O为△BCE的外接圆，点D为 $\hat{B D C}$ 上任意一点．若AE=AC=2n ， BC=n²－1，BE=n²－2n+1 ．(n≥2，且n为正整数) ．

(1)、求证：∠CAE+∠CDE=90°；

(2)、①如图2，当CD过圆心O时，①将△ACD绕点A顺时针旋转得△AEF ，连接DF ，请补全图形，猜想CD、DE、DF之间的数量关系，并证明你的猜想；②若n=3，求AD的长．

查看试题解析
22. 如图，抛物线y=ax²－2ax+c与x轴分别交于点A、B(点B在点A的右侧)，与y轴交于点C ，连接BC ，点( $\frac{1}{2}$ ， $- \frac{3}{4}$ a－3)在抛物线上．

(1)、求c的值；

(2)、已知点D与C关于原点O对称，作射线BD交抛物线于点E ，若BD=DE ， ①求抛物线所对应的函数表达式；②过点B作BF⊥BC交抛物线的对称轴于点F ，以点C为圆心，以 $\sqrt{5}$ 的长为半径作⊙C ，点T为⊙C上的一个动点，求 $\frac{\sqrt{5}}{5}$ TB+TF的最小值．

查看试题解析