初中数学人教版八年级下学期期末考试复习专题:05特殊的平行四边形
试卷更新日期:2021-06-04 类型:复习试卷
一、单选题
-
1. 下面性质中菱形有而矩形没有的是( )A、邻角互补 B、内角和为360° C、对角线相等 D、对角线互相垂直2. 已知四边形ABCD是平行四边形,下列结论中错误的是( )A、当AB=BC时,四边形ABCD是菱形 B、当AC⊥BD时,四边形ABCD是菱形 C、当AC=BD时,四边形ABCD是矩形 D、当∠ABC=90°时,四边形ABCD是正方形3. 下列能够判定一个四边形是正方形的条件是( )
①一组邻边相等且对角线相等并互相平分;
②对角线互相垂直平分;
③四条边相等且四个内角也相等;
④对角线相等的菱形.
A、①②④ B、①③④ C、③④ D、①②③④4. 如图,在菱形ABCD中,对角线BD=4,AC=3BD,则菱形ABCD的面积为( ) A、96 B、48 C、24 D、65. 如图,在菱形ABCD中,AC与BD相交于点O,点P是AB的中点,PO=2,则菱形ABCD的周长是( )
A、96 B、48 C、24 D、65. 如图,在菱形ABCD中,AC与BD相交于点O,点P是AB的中点,PO=2,则菱形ABCD的周长是( )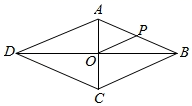 A、4 B、8 C、16 D、246. 菱形ABCD的周长为36,其相邻两内角的度数比1:5,则此菱形的面积为( )A、40.5 B、20.25 C、45 D、22.57. 如图,在矩形 中, 、 相交于点 , 平分 交 于点 ,若 ,则 的度数为( )
A、4 B、8 C、16 D、246. 菱形ABCD的周长为36,其相邻两内角的度数比1:5,则此菱形的面积为( )A、40.5 B、20.25 C、45 D、22.57. 如图,在矩形 中, 、 相交于点 , 平分 交 于点 ,若 ,则 的度数为( ) A、60° B、75° C、72° D、90°8. 如图,在菱形 中, 相交于 , , 是线段 上一点,则 的度数可能是( )
A、60° B、75° C、72° D、90°8. 如图,在菱形 中, 相交于 , , 是线段 上一点,则 的度数可能是( ) A、 B、 C、 D、9. 四边形ABCD为平行四边形,延长AD到点E , 使DE=AD , 连接EB , EC , DB . 添加一个条件,不能使四边形DBCE成为矩形的是( )
A、 B、 C、 D、9. 四边形ABCD为平行四边形,延长AD到点E , 使DE=AD , 连接EB , EC , DB . 添加一个条件,不能使四边形DBCE成为矩形的是( ) A、DB=DE B、AB=BE C、∠ADB=90° D、CE⊥DE10. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,则下列说法不一定成立的是( )
A、DB=DE B、AB=BE C、∠ADB=90° D、CE⊥DE10. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,则下列说法不一定成立的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,两个长宽分别为7cm、3cm的矩形如图叠放在一起,则图中阴影部分的面积是 .
 12. 如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE=°.
12. 如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE=°.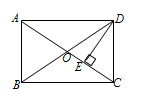 13. 如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E=度.
13. 如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E=度. 14. 如图,在矩形ABCD中,BC=40cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和1cm/s,则最快s后,四边ABPQ成为矩形.
14. 如图,在矩形ABCD中,BC=40cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和1cm/s,则最快s后,四边ABPQ成为矩形. 15. 如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则 的值为 .
15. 如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则 的值为 . 16. 如图,直线过正方形ABCD的顶点B,点A、C到直E的距离分别是1和2,则正方形ABCD面积是.
16. 如图,直线过正方形ABCD的顶点B,点A、C到直E的距离分别是1和2,则正方形ABCD面积是.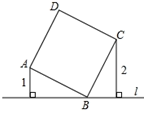
三、解答题