广东省佛山市顺德区2021年中考数学一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
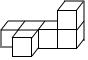
1. 2020年,我国脱贫攻坚战取得了全面胜利,现行标准下的9899万农村贫困人口全部脱贫,其中9899万用科学记数法表示为( )A、 B、 C、 D、2. 如图所示的几何体是由几个大小相同的小正方体搭成的,其俯视图是( )
 A、
A、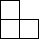 B、
B、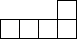 C、
C、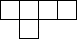 D、
D、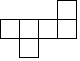 3. 下列运算正确的是( )A、 B、 C、 D、4. 为了估计某地区梅花鹿的数量,先捕捉20只梅花鹿做上标记,然后放走,待有标记的梅花鹿完全混合于鹿群后,第二次捕捉100只梅花鹿,发现其中5只有标记.估计这个地区的梅花鹿的数量约有( )只.A、200 B、300 C、400 D、5005. 已知 介于两个连续自然数之间,则下列结论正确的是( )A、 B、 C、 D、6. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 为了估计某地区梅花鹿的数量,先捕捉20只梅花鹿做上标记,然后放走,待有标记的梅花鹿完全混合于鹿群后,第二次捕捉100只梅花鹿,发现其中5只有标记.估计这个地区的梅花鹿的数量约有( )只.A、200 B、300 C、400 D、5005. 已知 介于两个连续自然数之间,则下列结论正确的是( )A、 B、 C、 D、6. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( )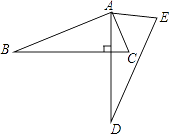 A、60° B、75° C、85° D、90°7. 如图,E是平行四边形 边 延长线上一点,且 ,连接 、 、 .若 ,则四边形 是( )
A、60° B、75° C、85° D、90°7. 如图,E是平行四边形 边 延长线上一点,且 ,连接 、 、 .若 ,则四边形 是( ) A、平行四边形 B、矩形 C、菱形 D、正方形8. 如图,一次函数 的图象与反比例函数 的图象的一个交点为 ,则不等式 的解集是( )
A、平行四边形 B、矩形 C、菱形 D、正方形8. 如图,一次函数 的图象与反比例函数 的图象的一个交点为 ,则不等式 的解集是( ) A、 B、 C、 D、 或9. 如图, 为 的直径,C、D为 上两点, ,则 的长度为( )
A、 B、 C、 D、 或9. 如图, 为 的直径,C、D为 上两点, ,则 的长度为( ) A、3 B、4 C、5 D、610. 若关于x的不等式组 有且只有8个整数解,关于y的方程 的解为非负数,则满足条件的整数a的值为( )A、 B、 C、 或 D、 或 或
A、3 B、4 C、5 D、610. 若关于x的不等式组 有且只有8个整数解,关于y的方程 的解为非负数,则满足条件的整数a的值为( )A、 B、 C、 或 D、 或 或二、填空题
-
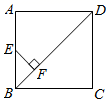
11. 因式分解: .12. 若关于x的一元二次方程x²-2x+c=0没有实数根.则实数c取值范围是13. 如果一个正多边形每一个内角都等于 ,那么这个正多边形的内角和是 .14. 在边长为2的正方形 中,点E是 的中点, 于点F , 则 的长度 .
 15. 某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其它几个班的参赛作品情况及获奖情况绘制在图1和图2两幅尚不完整的统计图中,则获奖率最高的班级是 .
15. 某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其它几个班的参赛作品情况及获奖情况绘制在图1和图2两幅尚不完整的统计图中,则获奖率最高的班级是 . 16. 如图,在A点有一个热气球,由于受西风的影响,以20米/分的速度沿与地面成 角的方向飞行,10分钟后到达C处,此时热气球上的人测得地面上的B点俯角为 ,则A、B两点间的距离为米.
16. 如图,在A点有一个热气球,由于受西风的影响,以20米/分的速度沿与地面成 角的方向飞行,10分钟后到达C处,此时热气球上的人测得地面上的B点俯角为 ,则A、B两点间的距离为米. 17. 如图,在四边形 中, .若 ,则 的内切圆面积(结果保留 ).
17. 如图,在四边形 中, .若 ,则 的内切圆面积(结果保留 ).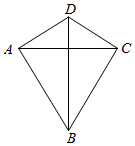
三、解答题
-
18. 计算: .19. 先化简,再计算: ,其中x满足 .20. 如图,M是 的半径 的中点,弦 于点M , 过点C作 交 的延长线于点D , 连接 .
 (1)、求 的值;(2)、求证: 是 的切线.21. 某历史文化街区需要加装一批垃圾分类提示牌和垃圾箱.根据需求,提示牌比垃圾箱多5个,且提示牌和垃圾箱的个数之和不少于100个,则至少购买垃圾箱多少个?22. 如图,在直角三角形 中, ,作 的内接矩形 .设 ,求x取何值时矩形的面积最大?
(1)、求 的值;(2)、求证: 是 的切线.21. 某历史文化街区需要加装一批垃圾分类提示牌和垃圾箱.根据需求,提示牌比垃圾箱多5个,且提示牌和垃圾箱的个数之和不少于100个,则至少购买垃圾箱多少个?22. 如图,在直角三角形 中, ,作 的内接矩形 .设 ,求x取何值时矩形的面积最大?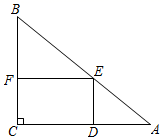 23. 如图,点A在反比例函数 (其中 )图象上, ,以点A为圆心, 长为半径画弧交x轴正半轴于点B .
23. 如图,点A在反比例函数 (其中 )图象上, ,以点A为圆心, 长为半径画弧交x轴正半轴于点B .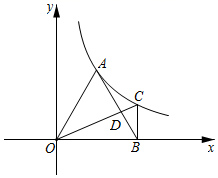 (1)、当 时,求k的值;(2)、过点B作 交反比例函数的图象于点C , 连接 交 于点D , 求 的值.24. 已知抛物线 : 交x轴于点A、B , 顶点为M , A、B、M关于原点的对称点分别是E、F、N .
(1)、当 时,求k的值;(2)、过点B作 交反比例函数的图象于点C , 连接 交 于点D , 求 的值.24. 已知抛物线 : 交x轴于点A、B , 顶点为M , A、B、M关于原点的对称点分别是E、F、N . (1)、求点A、B的坐标;(2)、求出经过E、且以N为顶点的抛物线 的表达式;(3)、抛物线 与y轴交点为D , 点P是抛物线 在第四象限部分上一动点,点Q是y轴上一动点,求出一组P、Q的值,使得以点D、P、Q为顶点的三角形与 相似.25. 在 中, ,点D是 边上的一点.
(1)、求点A、B的坐标;(2)、求出经过E、且以N为顶点的抛物线 的表达式;(3)、抛物线 与y轴交点为D , 点P是抛物线 在第四象限部分上一动点,点Q是y轴上一动点,求出一组P、Q的值,使得以点D、P、Q为顶点的三角形与 相似.25. 在 中, ,点D是 边上的一点.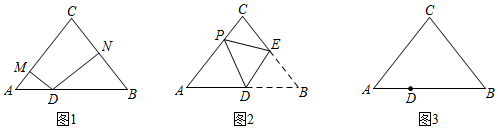 (1)、如图1,过点D作 于点M , 于点N , 求 的值;(2)、将 沿着过点D的直线折叠,使点B落在 边的点P处(不与点A、C重合),折痕交 边于点E;
(1)、如图1,过点D作 于点M , 于点N , 求 的值;(2)、将 沿着过点D的直线折叠,使点B落在 边的点P处(不与点A、C重合),折痕交 边于点E;①如图2,当点D是 的中点时,求 的长度;
②如图3,设 ,若存在两次不同的折痕,使点B落在 边上两个不同的位置,求a的取值范围.