广东省佛山市三水区2021年中考数学一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 有理数2021的相反数为( )A、2021 B、-2021 C、 D、2. 已知点A与点B关于原点对称,若点A的坐标为(﹣2,3),则点B的坐标是( )A、(﹣3,2) B、(﹣2,﹣3) C、(3,﹣2) D、(2,﹣3)3. 将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是( )A、
 B、
B、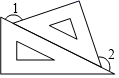 C、
C、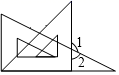 D、
D、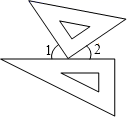 4. 甲袋中装有2张相同的卡片,颜色分别为红色和黄色;乙袋中装有3张相同的卡片,颜色分别为红色、黄色、绿色.从这两个口袋中各随机抽取1张卡片,取出的两张卡片中至少有一张是红色的概率是( )A、 B、 C、 D、5. 已知x>2,则下列二次根式定有意义的是( )A、 B、 C、 D、6. 尺规作图作角的平分线,作法步骤如下:
4. 甲袋中装有2张相同的卡片,颜色分别为红色和黄色;乙袋中装有3张相同的卡片,颜色分别为红色、黄色、绿色.从这两个口袋中各随机抽取1张卡片,取出的两张卡片中至少有一张是红色的概率是( )A、 B、 C、 D、5. 已知x>2,则下列二次根式定有意义的是( )A、 B、 C、 D、6. 尺规作图作角的平分线,作法步骤如下:①以点O为圆心,任意长为半径画弧,交OA、OB于C、D两点;
②分别以C、D为圆心,大于 CD长为半径画弧,两弧交于点P;
③过点P作射线OP , 射线OP即为所求.

则上述作法的依据是( )
A、SSS B、SAS C、AAS D、ASA7. 关于x的函数y=k(x﹣1)和y= (k≠0),它们在同一坐标系内的图象大致是( )A、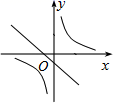 B、
B、 C、
C、 D、
D、 8. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
8. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( ) A、 B、6 C、4 D、59. 方程x2﹣6x+5=0的两个根之和为( )A、﹣6 B、6 C、﹣5 D、510. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=﹣1,下列结论错误的是( )
A、 B、6 C、4 D、59. 方程x2﹣6x+5=0的两个根之和为( )A、﹣6 B、6 C、﹣5 D、510. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=﹣1,下列结论错误的是( )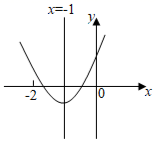 A、b2>4ac B、abc>0 C、a﹣c<0 D、am2+bm≥a﹣b(m为任意实数)
A、b2>4ac B、abc>0 C、a﹣c<0 D、am2+bm≥a﹣b(m为任意实数)二、填空题
-
11. 分解因式:25﹣x2=.12. 若某个正多边形的每一个外角都等于其相邻内角的 ,则这个正多边形的边数是 .13. 已知(a﹣3)2+|b﹣4|=0,则a+ 的值是 .14. 代数式2a2-b=7,则10-4a2+2b的值是15. 如图,已知AB是⊙O的直径,AB=2,C、D是圆周上的点,且sin∠CDB= ,则BC的长为。
 16. 如图,矩形 中, , ,点P在对角线 上,且 ,连接 并延长,交 的延长线于点Q,连接 ,则 的长为 .
16. 如图,矩形 中, , ,点P在对角线 上,且 ,连接 并延长,交 的延长线于点Q,连接 ,则 的长为 .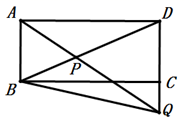 17. 如图,点A1 , A2 , A3 , A4 , A5 , …,在射线ON上,点B1 , B2 , B3 , B4 , …在射线OM上,点C1 , C2 , C3 , …分别在线段A2B2 , A3B3 , A4B4 , …上,且四边形A1B1C1A2 , 四边形A2B2C2A3 , 四边形A3B3C3A4 , …均为正方形,若OA1=4,A1B1=2,则正方形A2021B2021C2021D2022的边长为 .
17. 如图,点A1 , A2 , A3 , A4 , A5 , …,在射线ON上,点B1 , B2 , B3 , B4 , …在射线OM上,点C1 , C2 , C3 , …分别在线段A2B2 , A3B3 , A4B4 , …上,且四边形A1B1C1A2 , 四边形A2B2C2A3 , 四边形A3B3C3A4 , …均为正方形,若OA1=4,A1B1=2,则正方形A2021B2021C2021D2022的边长为 .
三、解答题
-
18. 计算: ×(﹣ )﹣|2 |+( )﹣3﹣(π﹣3.14)0 .19. 体育课上,老师为了解男学生定点投篮的情况,随机抽取8名男学生进行每人4次定点投篮的测试,进球数的统计如图所示.
 (1)、男生进球数的平均数为 , 中位数为 .(2)、投球4次,进球3个以上(含3个)为优秀,全校有男生1200人,估计为“优秀”等级的男生约为多少人?20. 如图,AB=AC , 直线l过点A , BM⊥直线l , CN⊥直线l , 垂足分别为M、N , 且BM=AN .
(1)、男生进球数的平均数为 , 中位数为 .(2)、投球4次,进球3个以上(含3个)为优秀,全校有男生1200人,估计为“优秀”等级的男生约为多少人?20. 如图,AB=AC , 直线l过点A , BM⊥直线l , CN⊥直线l , 垂足分别为M、N , 且BM=AN . (1)、求证△AMB≌△CNA;(2)、求证∠BAC=90°.21. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为提高学生的阅读品味,现决定购买《艾青诗选》和《格列佛游记》两种书共50本.已知购买2本《艾青诗选》和1本《格列佛游记》需100元;购买6本《艾青诗选》与购买7本《格列佛游记》的价格相同.(1)、求这两种书的单价;(2)、若购买《艾青诗选》的数盘不少于所购买《格列佛游记》数量的一半,且购买两种书的总价不超过1600元.请问有哪几种购买方案?22. 如图,AB是⊙O的直径,C为⊙O上一点,连接AC,CE⊥AB于点E,D是直径AB延长线上一点,且∠BCE=∠BCD.
(1)、求证△AMB≌△CNA;(2)、求证∠BAC=90°.21. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为提高学生的阅读品味,现决定购买《艾青诗选》和《格列佛游记》两种书共50本.已知购买2本《艾青诗选》和1本《格列佛游记》需100元;购买6本《艾青诗选》与购买7本《格列佛游记》的价格相同.(1)、求这两种书的单价;(2)、若购买《艾青诗选》的数盘不少于所购买《格列佛游记》数量的一半,且购买两种书的总价不超过1600元.请问有哪几种购买方案?22. 如图,AB是⊙O的直径,C为⊙O上一点,连接AC,CE⊥AB于点E,D是直径AB延长线上一点,且∠BCE=∠BCD. (1)、求证:CD是⊙O的切线;(2)、若AD=8, = ,求CD的长.23. 去年某商店“十一黄金周”进行促销活动期间,前六天的总营业额为450万元,第七天的营业额是前六天总营业额的12%.(1)、求该商店去年“十一黄金周”这七天的总营业额;(2)、去年,该商店7月份的营业额为350万元,8、9月份营业额的月增长率相同,“十一黄金周”这七天的总营业额与9月份的营业额相等.求该商店去年8、9月份营业额的月增长率.24. 如图,在平面直角坐标系中,正比例函数y=mx与反比例函数y= 的图象交于A、P(﹣ ,2 )两点,点B( ,3 )与点D关于直线AP对称,连接AB , 作CD∥y轴交直线AP于点C .
(1)、求证:CD是⊙O的切线;(2)、若AD=8, = ,求CD的长.23. 去年某商店“十一黄金周”进行促销活动期间,前六天的总营业额为450万元,第七天的营业额是前六天总营业额的12%.(1)、求该商店去年“十一黄金周”这七天的总营业额;(2)、去年,该商店7月份的营业额为350万元,8、9月份营业额的月增长率相同,“十一黄金周”这七天的总营业额与9月份的营业额相等.求该商店去年8、9月份营业额的月增长率.24. 如图,在平面直角坐标系中,正比例函数y=mx与反比例函数y= 的图象交于A、P(﹣ ,2 )两点,点B( ,3 )与点D关于直线AP对称,连接AB , 作CD∥y轴交直线AP于点C .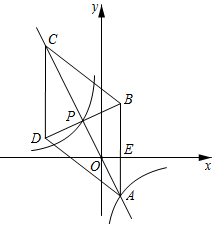 (1)、求m、n的值和点A的坐标;(2)、求sin∠CDB的值;(3)、连接AD、BC , 求四边形ABCD的面积.25. 如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣ ,0),B(2,0)两点,与y轴交于点C(0,1).
(1)、求m、n的值和点A的坐标;(2)、求sin∠CDB的值;(3)、连接AD、BC , 求四边形ABCD的面积.25. 如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣ ,0),B(2,0)两点,与y轴交于点C(0,1). (1)、求抛物线的函数表达式;(2)、如图1,点D为第一象限内抛物线上一点,连接AD , BC交于点E , 求 的最大值;(3)、如图2,连接AC , BC , 过点O作直线l∥BC , 点P , Q分别为直线l和抛物线上的点.试探究:在第四象限内是否存在这样的点P , 使△BPQ∽△CAB . 若存在,请直接写出所有符合条件的点P的坐标,若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、如图1,点D为第一象限内抛物线上一点,连接AD , BC交于点E , 求 的最大值;(3)、如图2,连接AC , BC , 过点O作直线l∥BC , 点P , Q分别为直线l和抛物线上的点.试探究:在第四象限内是否存在这样的点P , 使△BPQ∽△CAB . 若存在,请直接写出所有符合条件的点P的坐标,若不存在,请说明理由.