北京市延庆区2021年中考数学一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 中国财政部2021年3月18日发布数据显示,前2个月,全国一般公共预算收入约为41800亿元,将41800用科学记数法表示应为( )A、 B、 C、 D、2. 如图是某几何体的三视图,该几何体是( )
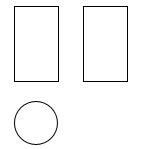 A、正方体 B、圆锥 C、四棱柱 D、圆柱3. 五边形的外角和等于( )
A、正方体 B、圆锥 C、四棱柱 D、圆柱3. 五边形的外角和等于( )
A、180° B、360 ° C、540° D、720°4. 下列给出的等边三角形、圆、平行四边形、矩形中是轴对称图形而不是中心对称图形的是( )A、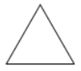 B、
B、 C、
C、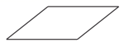 D、
D、 5. 如图,直线 ,点A,C,D分别是 , 上的点,且 于点A,若 ,则 的度数为( )
5. 如图,直线 ,点A,C,D分别是 , 上的点,且 于点A,若 ,则 的度数为( ) A、30° B、50° C、60° D、70°6. 一个不透明的盒子中装有4个除颜色外都相同的小球,其中3个是白球,1个是红球,从中随机同时摸出两个小球,那么摸出小球的颜色不同的概率为( )A、 B、 C、 D、7. 如图,数轴上两点 所对应的实数分别为 ,则 的结果可能是( )
A、30° B、50° C、60° D、70°6. 一个不透明的盒子中装有4个除颜色外都相同的小球,其中3个是白球,1个是红球,从中随机同时摸出两个小球,那么摸出小球的颜色不同的概率为( )A、 B、 C、 D、7. 如图,数轴上两点 所对应的实数分别为 ,则 的结果可能是( )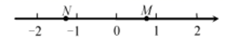 A、 B、1 C、2 D、38. 2020年12月1日下午6点,京张高铁延庆线正式启用,“复兴号”列车在北京北站与延庆站之间往返,途径清河站、昌平站、八达岭站.下图是从北京北站到延庆站的线路图,其中延庆站到八达岭站,全长 公里.某天“复兴号”列车从八达岭站出发,终点为北京北.列车始终以每小时160公里的速度匀速行驶,那么在到达昌平站之前,“复兴号”列车到延庆站的距离与对应的行驶的时间满足的函数关系是( )
A、 B、1 C、2 D、38. 2020年12月1日下午6点,京张高铁延庆线正式启用,“复兴号”列车在北京北站与延庆站之间往返,途径清河站、昌平站、八达岭站.下图是从北京北站到延庆站的线路图,其中延庆站到八达岭站,全长 公里.某天“复兴号”列车从八达岭站出发,终点为北京北.列车始终以每小时160公里的速度匀速行驶,那么在到达昌平站之前,“复兴号”列车到延庆站的距离与对应的行驶的时间满足的函数关系是( ) A、正比例函数关系 B、反比例函数关系 C、一次函数关系 D、二次函数关系
A、正比例函数关系 B、反比例函数关系 C、一次函数关系 D、二次函数关系二、填空题
-
9. 函数 中自变量x的取值范围是 .10. 方程组 的解为 .11. 分解因式: .12. 请写出一个大于1且小于2的无理数:.13. 如图, 是 的弦,C是 上的一点,且 , 于点E,交 于点D.若 的半径为6,则弦 的长为 .
 14. 如果 时,那么代数式 的值 .15. 如图所示, 是放置在正方形网格中的一个角,则 的值是 .
14. 如果 时,那么代数式 的值 .15. 如图所示, 是放置在正方形网格中的一个角,则 的值是 . 16. 把图1中边长为10的菱形沿对角线分成四个全等的直角三角形,且此菱形的一条对角线长为16,将这四个直角三角形拼成如图2所示的正方形,则图2中的阴影的面积为 .
16. 把图1中边长为10的菱形沿对角线分成四个全等的直角三角形,且此菱形的一条对角线长为16,将这四个直角三角形拼成如图2所示的正方形,则图2中的阴影的面积为 .
三、解答题
-
17. 计算: .18. 解不等式组: .19. 关于x的一元二次方程 有实数根.(1)、求m的取值范围;(2)、若m为正整数,求出此时方程的根.20. 如图,在 中, .

求作:线段 ,使得点D在线段 上,且 .
作法:①分别以点A,B为圆心,大于 长为半径作弧,两弧相交于点M,N两点;
②做直线 ,交 于点D;
③连接 .
所以线段 即为所求的线段.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:∵ , ,
∴ 是 的垂直平分线.()(填推理的依据)
∴点 是 的中点.
∵ ,
∴ .()(填推理的依据)
21. 小林和小明在信息技术课上设计了一个小游戏程序:开始时两人的屏幕上显示的数分别是9和4,如图.每按一次屏幕,小林的屏幕上的数就会加上 ,同时小明的屏幕上的数就会减去 ,且均显示化简后的结果.如下表就是按一次后及两次后屏幕显示的结果.
开始数
按一次后
按二次后
按三次后
按四次后
小林
9
小明
4
根据以上的信息回答问题:从开始起按4次后,
(1)、两人屏幕上显示的结果是:小林;小明;(2)、判断这两个结果的大小,并说明理由.22. 如图,在 中, , ,垂足为D,过点A作 ,且 ,连接 ,交 于点F,连接 . (1)、求证:四边形 为矩形;(2)、若 ,求 的长.23. 如图,在平面直角坐标系 中,一次函数 由函数 平移得到,且与函数 的图象交于点 .
(1)、求证:四边形 为矩形;(2)、若 ,求 的长.23. 如图,在平面直角坐标系 中,一次函数 由函数 平移得到,且与函数 的图象交于点 . (1)、求一次函数的表达式;(2)、已知点 ,过点P作平行于y轴的直线,交直线 于点 ,交函数 的图象于点 .当 时,直接写出n的取值范围.24. 如图, 是 的直径, 为 的切线,切点为C,交 的延长线于点A,点F是 上的一点,且点C是弧 的中点,连接 并延长交 的延长线于点B.
(1)、求一次函数的表达式;(2)、已知点 ,过点P作平行于y轴的直线,交直线 于点 ,交函数 的图象于点 .当 时,直接写出n的取值范围.24. 如图, 是 的直径, 为 的切线,切点为C,交 的延长线于点A,点F是 上的一点,且点C是弧 的中点,连接 并延长交 的延长线于点B. (1)、求证: ;(2)、若 , ,求 的半径.25. 在世园会开幕一周年之际,延庆区围绕“践行‘两山’理论,聚力冬奥筹办,建设美丽延庆”主题,同筑生态文明.近年来,在延庆区政府的积极治理下,空气质量得到极大改善.下图是根据延庆区环境保护局公布的2014~2020年各年的全年空气质量优良天数绘制的折线统计图.
(1)、求证: ;(2)、若 , ,求 的半径.25. 在世园会开幕一周年之际,延庆区围绕“践行‘两山’理论,聚力冬奥筹办,建设美丽延庆”主题,同筑生态文明.近年来,在延庆区政府的积极治理下,空气质量得到极大改善.下图是根据延庆区环境保护局公布的2014~2020年各年的全年空气质量优良天数绘制的折线统计图.
请结合统计图解答下列问题:
(1)、2020年比2016年的全年空气质量优良天数增加了天;(2)、这七年的全年空气质量优良天数的中位数是;(3)、在生态环境部2月25日举行的例行新闻发布会上透露,“十四五”空气质量改善目标指标设置仍然坚持PM和优良天数两个指标;其中,全国优良天数达标指标将提升至 %.截止到3月31日,延庆区2021年空气质量优良天数如下:月份
1月(31天)
2月(28天)
3月(31天)
优良天数/天
28
25
28
①该小区2021年1月1日至3月31日的空气质量优良天数的平均数约为 ▲ .
②试根据以上信息预测延庆区2021年(共365天)全年空气质量优良天数能否达标?达标的天数约为多少天?
26. 在平面直角坐标系 中,直线 与 y轴交于点A,与x轴交于点B,二次函数的图象过A,B两点,且与x轴的另一交点为点 C, ; (1)、求点C的坐标;(2)、对于该二次函数图象上的任意两点 , ,当 时,总有 .
(1)、求点C的坐标;(2)、对于该二次函数图象上的任意两点 , ,当 时,总有 .①求二次函数的表达式;
②设点A在抛物线上的对称点为点D,记抛物线在C,D之间的部分为图象G(包含C, D两点).若一次函数 的图象与图象G有公共点,结合函数图象,求 k的取值范围.
27. 在正方形 中,点E在射线 上(不与点B、C重合),连接 , ,将 绕点E逆时针旋转90°得到 ,连接 .
 (1)、如图1,点E在 边上.
(1)、如图1,点E在 边上.①依题意补全图1;
②若 , ,求 的长;
(2)、如图2,点E在 边的延长线上,用等式表示线段 , , 之间的数量关系.28. 规定如下:图形M与图形N恰有两个公共点(这两个公共点不重合),则称图形M与图形N是和谐图形.(1)、在平面直角坐标系 中,已知 的半径为2,若直线 与 是和谐图形,请你写出一个满足条件的k值,即 ;(2)、在平面直角坐标系 中,已知点 ,直线 与x轴、y轴分别交于B,C两点(其中点A不与点B重合),则线段 与直线l组成的图形我们称为图形V;① 时,以A为圆心,r为半径的 与图形V是和谐图形,求r的取值范围;
②以点A为圆心, 为半径的 与图形V均组成和谐图形,求t的取值范围.