北京市顺义区2021年中考数学一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 我国首次火星探测任务被命名为“天问一号”2021年3月26日,国家航天局发布两幅由天问一号探测器拍摄的南、北半球火星侧身影像.该影像是探测器飞行至距离火星11000公里处利用中分辨率相机拍摄的.将11000用科学记数法表示应为( )A、 B、 C、 D、2. 下列立体图形中俯视图是三角形的是( )A、
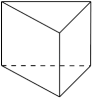
B、
B、
C、
C、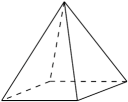
D、
D、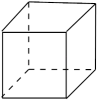
3. 实数a , b在数轴上对应点的位置如图所示,则下列结论正确的是( )
3. 实数a , b在数轴上对应点的位置如图所示,则下列结论正确的是( ) A、 B、 C、 D、4. 若正多边形的一个外角的度数为40°,则这个正多边形的边数为( )A、7 B、8 C、9 D、105. 不透明的袋子中装有6个球除颜色外无其他差别,其中有1个红球,2个黄球,3个绿球从袋子中随机摸出一个球.那么摸出的球是红球的概率是( )A、 B、 C、 D、6. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
A、 B、 C、 D、4. 若正多边形的一个外角的度数为40°,则这个正多边形的边数为( )A、7 B、8 C、9 D、105. 不透明的袋子中装有6个球除颜色外无其他差别,其中有1个红球,2个黄球,3个绿球从袋子中随机摸出一个球.那么摸出的球是红球的概率是( )A、 B、 C、 D、6. 下列图形中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 将一个长为 ,宽为 的矩形纸片 ,用剪刀沿图1中的虚线剪开,分成四块形状和大小都一样的小矩形纸片,然后按图2的方式拼成一个正方形,则中间小正方形的面积为( )
7. 将一个长为 ,宽为 的矩形纸片 ,用剪刀沿图1中的虚线剪开,分成四块形状和大小都一样的小矩形纸片,然后按图2的方式拼成一个正方形,则中间小正方形的面积为( ) A、 B、 C、 D、8. 已知y是x的函数,下表是x与y的几组对应值:
A、 B、 C、 D、8. 已知y是x的函数,下表是x与y的几组对应值:x
…
3
6
…
y
…
2
1
…
对于y与x的函数关系有以下4个描述①可能是正比例函数关系;②可能是一次函数关系;③可能是反比例函数关系;④可能是二次函数关系.所有正确的描述是( )
A、①② B、②③ C、③④ D、①④二、填空题
-
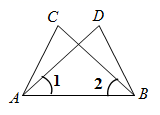
9. 若代数式 有意义,则实数a的取值范围是 .10. 已知方程组的解为 ,写出一个满足条件的方程组 .11. 如图, ,只需添加一个条件即可证明 ,这个条件可以是(写出一个即可)
 12. 如图,已知A , B , C是 上三点, ,则 的度数为 .
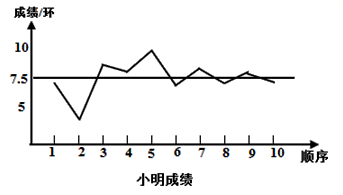
12. 如图,已知A , B , C是 上三点, ,则 的度数为 .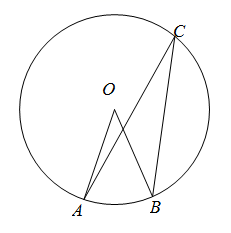 13. 要从小华、小明两名射击运动员中选择一名运动员参加射击比赛,在赛前对他们进行了一次选拔赛,下图为小华、小明两人在选拔赛中各射击10次成绩的折线图和表示平均数的水平线.你认为应该选择(填“小华”或“小明”)参加射击比赛;理由是 .
13. 要从小华、小明两名射击运动员中选择一名运动员参加射击比赛,在赛前对他们进行了一次选拔赛,下图为小华、小明两人在选拔赛中各射击10次成绩的折线图和表示平均数的水平线.你认为应该选择(填“小华”或“小明”)参加射击比赛;理由是 .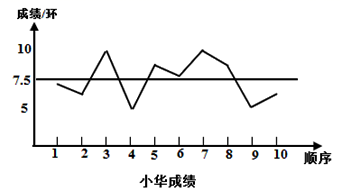
 14. 写出一个反比例函数表达式,使它的图象与直线 有公共点,这个函数的表达式为 .15. 如图所示的网格是正方形网格,点A , B , C , D , E , F是网格线的交点,则 的面积与 的面积比为 .
14. 写出一个反比例函数表达式,使它的图象与直线 有公共点,这个函数的表达式为 .15. 如图所示的网格是正方形网格,点A , B , C , D , E , F是网格线的交点,则 的面积与 的面积比为 . 16. 标有1-25号的25个座位如图摆放.甲、乙、丙、丁四人玩选座位游戏,甲选2个座位,乙选3个座位,丙选4个座位,丁选5个座位,游戏规则如下:①每人只能选择同一横行或同一竖列的座位;②每人使自己所选的座位号数字之和最小;③座位不能重复选择.如果按“甲、乙、丙、丁”的先后顺序选座位,那么甲选1,2号座位,乙选3,4,5号座位,丙选7,8,9,10号座位,丁选13,14,15,16,17号座位,此时四人所选的座位号数字之和为124,如果按“丁、丙、乙、甲”的先后顺序选座位,那么四人所选的座位号数字之和为 .
16. 标有1-25号的25个座位如图摆放.甲、乙、丙、丁四人玩选座位游戏,甲选2个座位,乙选3个座位,丙选4个座位,丁选5个座位,游戏规则如下:①每人只能选择同一横行或同一竖列的座位;②每人使自己所选的座位号数字之和最小;③座位不能重复选择.如果按“甲、乙、丙、丁”的先后顺序选座位,那么甲选1,2号座位,乙选3,4,5号座位,丙选7,8,9,10号座位,丁选13,14,15,16,17号座位,此时四人所选的座位号数字之和为124,如果按“丁、丙、乙、甲”的先后顺序选座位,那么四人所选的座位号数字之和为 .
三、解答题
-
17. 计算: .18. 解不等式: ,并把它的解集在数轴上表示出来.19. 已知 ,求代数式 的值.20. 已知:如图,射线 .

求作: ,使得点B在射线 上, , .
作法:①在射线 上任取一点M;
②以点M为圆心, 的长为半径画圆,交射线 于另一点B;
③以点A为圆心, 的长为半径画弧,在射线 的上方交 于点C;
④连接 、 .
所以 为所求作的三角形.
(1)、使用直尺和圆规依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:∵ 为 的直径,点C在 上,
∴ ()(填推理依据).
连接 .
∵ ,
∴ 为等边三角形()(填推理依据).
∴ .
21. 已知关于x的一元二次方程 .(1)、求证:方程总有两个不相等的实数根;(2)、若方程有一个根是1,求方程的另一个根.22. 如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.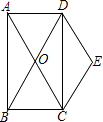 (1)、求证:四边形OCED是菱形;(2)、若∠BAC=30°,AC=4,求菱形OCED的面积.23. 在平面直角坐标系 中,一次函数 的图象经过点 .(1)、求k , b的值;(2)、当 时,对于x的每一个值,函数 的值小于一次函数 的值,直接写出n的取值范围.24. 如图, 是 的直径,弦 于点E , 的切线 交 的延长线于点F , 连接 , .
(1)、求证:四边形OCED是菱形;(2)、若∠BAC=30°,AC=4,求菱形OCED的面积.23. 在平面直角坐标系 中,一次函数 的图象经过点 .(1)、求k , b的值;(2)、当 时,对于x的每一个值,函数 的值小于一次函数 的值,直接写出n的取值范围.24. 如图, 是 的直径,弦 于点E , 的切线 交 的延长线于点F , 连接 , .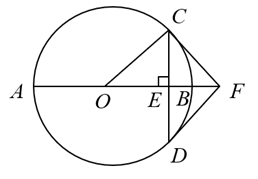 (1)、求证: 是 的切线;(2)、若 ,求 的长.25. 某校初三年级有400名学生,为了提高学生的体育锻炼兴趣,体育老师自主开发了一套体育锻炼方法,并在全年级实施.为了检验此种方法的锻炼效果,随机抽取了20名学生在应用此种方法锻炼前进行了第一次体育测试,应用此种方法锻炼一段时间后,又进行了第二次体育测试,获得了他们的成绩(满分30分),并对数据(成绩)进行整理描述和分析,下面给出了部分信息:
(1)、求证: 是 的切线;(2)、若 ,求 的长.25. 某校初三年级有400名学生,为了提高学生的体育锻炼兴趣,体育老师自主开发了一套体育锻炼方法,并在全年级实施.为了检验此种方法的锻炼效果,随机抽取了20名学生在应用此种方法锻炼前进行了第一次体育测试,应用此种方法锻炼一段时间后,又进行了第二次体育测试,获得了他们的成绩(满分30分),并对数据(成绩)进行整理描述和分析,下面给出了部分信息:a . 第一次体育测试成绩统计表:
分组/分
人数
1
1
9
m
3
b . 第二次体育测试成绩统计图:
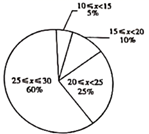
c . 两次成绩的平均数、中位数、众数如下:
平均数
中位数
众数
第一次成绩
19.7
n
19
第二次成绩
25
26.5
28
d . 第一次体育测试成绩在 这一组的数据是:
15,16,17,17,18,18,19,19,19
e . 第二次体育测试成绩在 这一组的数据是:17,19
请根据以上信息,回答下列问题:
(1)、 , ;(2)、求第二次体育测试成绩的及格率(大于或等于18分为及格);(3)、下列推断合理的是 .①第二次测试成绩的平均分高于第一次的平均分,所以大多数学生通过此种方法锻炼一段时间后成绩提升了.
②被抽测的学生小明的第二次测试成绩是24分,他觉得年级里大概有240人的测试成绩比他高,所以他决心努力锻炼提高身体素质.
26. 在平面直角坐标系 中,抛物线 与y轴交于点A .(1)、求点A和抛物线顶点的坐标(用含a的式子表示);(2)、直线 与抛物线 围成的区域(不包括边界)记作G . 横、纵坐标都为整数的点叫做整点.①当 时,结合函数图象,求区域G中整点的个数;
②当区域G中恰有6个整点时,直接写出a的取值范围.
27. 如图,等腰三角形 中, , 于点D , .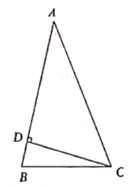 (1)、求出 的大小(用含 的式子表示);(2)、延长 至点E , 使 ,连接 并延长交 的延长线于点F .
(1)、求出 的大小(用含 的式子表示);(2)、延长 至点E , 使 ,连接 并延长交 的延长线于点F .①依题意补全图形;
②用等式表示线段 与 之间的数量关系,并证明.
28. 对于平面直角坐标系 中的 和图形N , 给出如下定义:如果 平移m个单位后,图形N上的所有点在 内或 上,则称m的最小值为 对图形N的“覆盖近距”.(1)、当 的半径为1时,①若点 ,则 对点A的“覆盖近距”为 ▲ ;
②若 对点B的“覆盖近距”为1,写出一个满足条件的点B的坐标 ▲ ;
③若直线 上存在点C , 使 对点C的“覆盖近距”为1,求b的取值范围;
(2)、当 的半径为2时, ,且 .记 对以 为对角线的正方形的“覆盖近距”为d , 直接写出d的取值范围.