北京市朝阳区2021年中考数学一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 中国首次火星探测任务天问一号探测器在2021年2月10日成功被火星捕获,成为中国第一颗人造火星卫星,并在距离火星约11000米处,拍摄了火星全景图像.将11000用科学记数法表示应为( )A、 B、 C、 D、2. 如图是某几何体的三视图,该几何体是( )
 A、长方体 B、三棱柱 C、三棱锥 D、圆锥3. 如图, 的度数为( )
A、长方体 B、三棱柱 C、三棱锥 D、圆锥3. 如图, 的度数为( )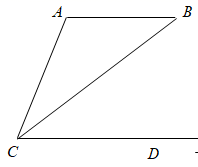 A、 B、 C、 D、4. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、角 B、等腰三角形 C、平行四边形 D、正六边形5. 实数a在数轴上的对应点的位置如图所示,若实数b满足 ,则b的值可以是( )
A、 B、 C、 D、4. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、角 B、等腰三角形 C、平行四边形 D、正六边形5. 实数a在数轴上的对应点的位置如图所示,若实数b满足 ,则b的值可以是( ) A、 B、0 C、1 D、26. 一个不透明的口袋中有四张卡片,上面分别写有数字 ,除数字外四张卡片无其他区别.随机从这个口袋中同时取出两张卡片,卡片上的数字之和等于5的概率是( )A、 B、 C、 D、7. 已知关于x的一元二次方程 有两个不相等的实数根,下列结论正确的是( )A、 B、 C、 D、8. 如图,一个小球由静止开始沿一个斜坡滚下,其速度每秒增加的值相同.用t表示小球滚动的时间, 表示小球的速度.下列图象中,能表示小球在斜坡上时 与 的函数关系的图象大致是( )
A、 B、0 C、1 D、26. 一个不透明的口袋中有四张卡片,上面分别写有数字 ,除数字外四张卡片无其他区别.随机从这个口袋中同时取出两张卡片,卡片上的数字之和等于5的概率是( )A、 B、 C、 D、7. 已知关于x的一元二次方程 有两个不相等的实数根,下列结论正确的是( )A、 B、 C、 D、8. 如图,一个小球由静止开始沿一个斜坡滚下,其速度每秒增加的值相同.用t表示小球滚动的时间, 表示小球的速度.下列图象中,能表示小球在斜坡上时 与 的函数关系的图象大致是( )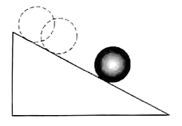 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 若 在实数范围内有意义,则实数x的取值范围是 .10. 写出一个比 大且比 小的整数 .11. 二元一次方程组 的解为 .12. 如图所示的正方形网格中, 是网格线交点,若 与 所在圆的圆心都为点O , 则 与 的长度之比为 .
 13. 如图, 中, ,点D是边 上的一个动点(点D与点 不重合),若再增加一个条件,就能使 与 相似,则这个条件可以是(写出一个即可).
13. 如图, 中, ,点D是边 上的一个动点(点D与点 不重合),若再增加一个条件,就能使 与 相似,则这个条件可以是(写出一个即可). 14. 如图,直线 与抛物线 交于点 ,且点A在y轴上,点B在x轴上,则不等式 的解集为 .
14. 如图,直线 与抛物线 交于点 ,且点A在y轴上,点B在x轴上,则不等式 的解集为 .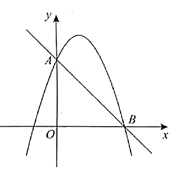 15. 如图,在四边形 中, 于点 .有如下四个结论:① ;② ;③ ;④ .上述结论中,所有正确结论的序号是 .
15. 如图,在四边形 中, 于点 .有如下四个结论:① ;② ;③ ;④ .上述结论中,所有正确结论的序号是 . 16. 某校初三年级共有8个班级的190名学生需要进行体检,各班学生人数如下表所示:
16. 某校初三年级共有8个班级的190名学生需要进行体检,各班学生人数如下表所示:班级
1班
2班
3班
4班
5班
6班
7班
8班
人数
29
19
25
23
22
27
21
24
若已经有7个班级的学生完成了体检,且已经完成体检的男生、女生的人数之比为 ,则还没有体检的班级可能是 .
三、解答题
-
17. 计算: .18. 解不等式组: .19. 解方程: .20. 已知 ,求代数式 的值.21. 已知:如图, 中, .
求作:线段 ,使得点D在线段 上,且 .
作法:①以点A为圆心, 长为半径画圆;
②以点C为圆心, 长为半径画弧,交 于点P(不与点B重合);
③连接 交 于点D . 线段 就是所求作的线段.
 (1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接 .
,
∴点C在 上.
点P在 上,
()(填推理的依据).
,
.
.
22. 如图,在矩形 中,对角线AC , BD相交于点O , 过点C作 ,交 的延长线于点E . (1)、求证: ;(2)、连接 ,若AB=2,tan∠ACD=2,求 的长.23. 如图,在平面直角坐标系 中, 是直线 与函数 的图象G的交点.
(1)、求证: ;(2)、连接 ,若AB=2,tan∠ACD=2,求 的长.23. 如图,在平面直角坐标系 中, 是直线 与函数 的图象G的交点. (1)、①求a的值;
(1)、①求a的值;②求函数 的解析式.
(2)、过点 且垂直于x轴的直线与直线 和图象G的交点分别为 ,当 时,直接写出n的取值范围.24. 如图, 中, ,点E在 上,以 为直径的 与 相切于点D , 与 相交于点F , 连接 . (1)、求证: ;(2)、若 ,求 的半径.25. 某地农业科技部门积极助力家乡农产品的改良与推广,为了解甲、乙两种新品橙子的质量,进行了抽样调查.在相同条件下,随机抽取了甲、乙各25份样品,对大小、甜度等各方面进行了综合测评,并对数据进行收集、整理、描述和分析,下面给出了部分信息.
(1)、求证: ;(2)、若 ,求 的半径.25. 某地农业科技部门积极助力家乡农产品的改良与推广,为了解甲、乙两种新品橙子的质量,进行了抽样调查.在相同条件下,随机抽取了甲、乙各25份样品,对大小、甜度等各方面进行了综合测评,并对数据进行收集、整理、描述和分析,下面给出了部分信息.a.测评分数(百分制)如下:
甲77 79 80 80 85 86 86 87 88 89 89 90 91 91 91 91 91
92 93 95 95 96 97 98 98
乙69 79 79 79 86 87 87 89 89 90 90 90 90 90 91 92 92
92 94 95 96 96 97 98 98
b.按如下分组整理、描述这两组样本数据:

甲
0
2
9
14
乙
1
3
5
16
c.甲、乙两种橙子测评分数的平均数、众数、中位数如下表所示:
品种
平均数
众数
中位数
甲
89.4
m
91
乙
89.4
90
n
根据以上信息,回答下列问题:
(1)、写出表中 的值;(2)、记甲种橙子测评分数的方差为 ,乙种橙子测评分数的方差为 ,则 的大小关系为;(3)、根据抽样调查情况,可以推断种橙子的质量较好,理由为 .(至少从两个不同的角度说明推断的合理性)
26. 如图,在等腰三角形 中, 为 边的中点,将线段 绕点A逆时针旋转 得到线段 ,连接 交 于点F .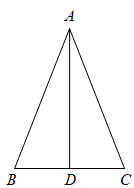 (1)、依题意补全图形;(2)、求 的度数;(3)、用等式表示线段 之间的数量关系,并证明.27. 在平面直角坐标系 中,抛物线 的对称轴是直线 .(1)、求抛物线 的顶点坐标;(2)、当 时,y的最大值是5,求a的值;(3)、在(2)的条件下,当 时,y的最大值是m , 最小值是n , 且 ,求t的值.28. 对于平面直角坐标系 中的图形M和点P , 给出如下定义:将图形M绕点P顺时针旋转 得到图形N , 图形N称为图形M关于点P的“垂直图形”.例如,图1中点D为点C关于点P的“垂直图形”.
(1)、依题意补全图形;(2)、求 的度数;(3)、用等式表示线段 之间的数量关系,并证明.27. 在平面直角坐标系 中,抛物线 的对称轴是直线 .(1)、求抛物线 的顶点坐标;(2)、当 时,y的最大值是5,求a的值;(3)、在(2)的条件下,当 时,y的最大值是m , 最小值是n , 且 ,求t的值.28. 对于平面直角坐标系 中的图形M和点P , 给出如下定义:将图形M绕点P顺时针旋转 得到图形N , 图形N称为图形M关于点P的“垂直图形”.例如,图1中点D为点C关于点P的“垂直图形”. (1)、点A关于原点O的“垂直图形”为点B .
(1)、点A关于原点O的“垂直图形”为点B .①若点A的坐标为 ,则点B的坐标为;
②若点B的坐标为 ,则点A的坐标为 .
(2)、 .线段 关于点G的“垂直图形”记为 ,点E的对应点为 ,点F的对应点为 .①求点 的坐标(用含a的式子表示);
②若 的半径为 , 上任意一点都在 内部或圆上,直接写出满足条件的 的长度的最大值.