安徽省合肥市包河区2021年中考数学一模试卷

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 数1，0， $- \frac{3}{2}$ ，-1中最小的是（）

A、1 B、0 C、 $- \frac{3}{2}$ D、-1

查看试题解析
2. 下列运算正确的是（　　）

A、a³+a³=a⁶ B、（3ab）²=6ab² C、a⁶÷a²=a³ D、（﹣a³）²=a⁶

查看试题解析
3. 因疫情影响，2020年合肥新桥机场全年旅客吞吐量为859.4万人次，同比下降30%，但仍高出全国机场运输平均水平6.6个百分点．数字859.4万用科学记数法表示正确的是（）

A、 $8.594 \times 10^{6}$ B、 $859.4 \times 10^{4}$ C、 $8.594 \times 10^{7}$ D、 $8.594 \times 10^{10}$

查看试题解析
4. 如图所示的几何体是由5个相同的小正方体构成，关于该几何体的三视图，下列说法错误的是（）

A、主视图是轴对称图形 B、左视图是轴对称图形 C、俯视图是轴对称图形 D、主视图和俯视图面积相等

查看试题解析
5. 已知正比例函数 $y_{1}$ 的图象与反比例函数 $y_{2}$ 的图象相交，其中一个交点坐标为 $(3 ， 4)$ ，当 $y_{1} < y_{2}$ 时，下列结论正确的是（）

A、 $- 3 < x < 0$ 或 $x > 3$ B、 $x < - 3$ 或 $0 < x < 3$ C、 $- 3 < x < 3$ D、 $x < - 4$ 或 $0 < x < 4$

查看试题解析
6. 某市2019年年底自然保护区覆盖率为15%，经过两年努力，预计该市2021年年底自然保护区覆盖率将会达到21.6%，则该市这两年自然保护区面积的平均增长率为（）

A、25% B、20% C、6.6% D、3.3%

查看试题解析
7. 如图，点P为 $∠ M O N$ 的平分线上一点， $∠ A P B$ 的两边分别与射线 $O M ， O N$ 交于 $A ， B$ 两点， $∠ A P B$ 绕点P旋转时始终满足 $O A \cdot O B = O P^{2}$ ，若 $∠ M O N = 54 °$ ，则 $∠ A P B$ 的度数为（）

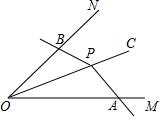A、153° B、144° C、163° D、162°

查看试题解析
8. 有三把外观一样但型号不同的锁，各配有一把钥匙．现遗失一把钥匙，用剩余的两把钥匙各随机从三把锁中选一把开锁一次，两次都不能打开的概率为（）

A、 $\frac{1}{9}$ B、 $\frac{1}{3}$ C、 $\frac{4}{9}$ D、 $\frac{2}{3}$

查看试题解析
9. 已知 $a ， b$ 为实数，且满足 $a b > 0 ， a + b - 2 = 0$ ，当a-b为整数时，ab的值为（）

A、 $\frac{3}{4}$ 或 $\frac{1}{2}$ B、 $\frac{1}{4}$ 或1 C、 $\frac{3}{4}$ 或1 D、 $\frac{1}{4}$ 或 $\frac{3}{4}$

查看试题解析
10. 如图①，在菱形 $A B C D$ 中，∠A=120°，点E是边 $B C$ 的中点，点F是对角线 $B D$ 上一动点，设 $F D$ 的长为x， $E F$ 与 $C F$ 长度的和为y．图②是y关于x的函数图象，点P为图象上的最低点，则函数图象的右端点Q的坐标为（）

A、 $(6 ， 4 \sqrt{3})$ B、 $(4 \sqrt{3} ， 3 \sqrt{3})$ C、 $(4 \sqrt{3} ， 6)$ D、 $(6 ， 3 \sqrt{3})$

查看试题解析

二、填空题

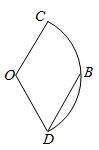
11. -64的立方根是。

查看试题解析
12. 用一组 $a ， b ， c$ 的值说明命题“若 $a > b$ ，则 $a c > b c$ ”是假命题，这组值可以是．（按 $a ， b ， c$ 的顺序填写）

查看试题解析
13. 如图，有一块半径为1米的扇形铁皮 $O C D$ ，取弧 $C D$ 的中点B，连接 $B D$ ，若 $O C / / B D$ ，则这块扇形铁皮的面积为平方米．

查看试题解析
14. 在平在直角坐标系中，已知抛物线 $y_{1} = a x^{2} + 3 a x - 4 a$ （a是常数，且 $a < 0$ ），直线 $A B$ 过点 $(0 ， n) (- 5 < n < 5)$ 且垂直于y轴．

(1)、该抛物线顶点的纵坐标为（用含a的代数式表示）；

(2)、当 $a = - 1$ 时，沿直线 $A B$ 将该抛物线在直线上方的部分翻折，其余部分不变，得到新图象G，图象G对应的函数记为 $y_{2}$ ，且当 $- 5 \leq x \leq 2$ 时，函数 $y_{2}$ 的最大值与最小值之差小于7，则n的取值范围为：．

查看试题解析

三、解答题

15. 计算： $\sqrt{18} + | 1 - \sqrt{2} | - {(\frac{1}{2})}^{- 1}$ ．

查看试题解析
16. 某农业公司原有葡萄园50亩，荷塘112亩，因葡萄热销，为了增加收入，该公司计划把部分荷塘改造为葡萄园，使葡萄园面积占荷塘面积的80%．求应把多少亩荷塘改造为葡萄园．

查看试题解析
17. 观察下列等式：
第1个等式： $1 + \frac{1}{1} = \frac{4}{3} \times (1 + \frac{1}{2})$ ；

第2个等式： $1 + \frac{1}{2} = \frac{9}{8} \times (1 + \frac{1}{3})$ ；

第3个等式： $1 + \frac{1}{3} = \frac{16}{15} \times (1 + \frac{1}{4})$ ；

第4个等式： $1 + \frac{1}{4} = \frac{25}{24} \times (1 + \frac{1}{5})$ ；

…

根据你观察到的规律，解决下列问题：

(1)、请写出第5个等式：；

(2)、请写出第n个等式：（用含n的等式表示），并证明．

查看试题解析
18. 如图，在平面直角坐标系中，已知 $Δ A B C$ 的三个顶点坐标分别是 $A (5 ， 4) ， B (1 ， 1) ， C (5 ， 1)$ ．

⑴请画出 $Δ A B C$ 关于x轴对称的 $Δ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ 的坐标；

⑵以O为对称中心，画出 $Δ A B C$ 关于O成中心对称的图形 $Δ A^{'} B^{'} C^{'}$ ；

⑶请用无刻度的直尺画出 $∠ A B C$ 的平分线 $B Q$ （点Q在线段 $A C$ 上）（保留作图辅助线）．

查看试题解析
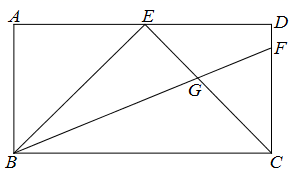
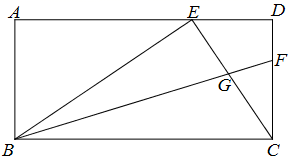
19. 如图，某大楼上树立一块高为3米的广告牌 $C D$ ．数学活动课上，立新老师带领小燕和小娟同学测量楼 $D H$ 的高．测角仪支架高 $A E = B F = 1.2$ 米，小燕在E处测得广告牌的顶点C的仰角为22°，小娟在F处测得广告牌的底部点D的仰角为45°， $A B = 45$ 米．请你根据两位同学测得的数据，求出楼 $D H$ 的高．（结果取整数，参考数据： $\sin 22 ° \approx 0.37 ， \cos 22 ° \approx 0.93 ， \tan 22 ° \approx 0.40$ ）

查看试题解析
20. 如图，AB是⊙O的直径，点E在弦AC的延长线上，过点E作ED⊥AE ， ED与⊙O相切于点D ．

(1)、求证：AD平分∠BAC；

(2)、若AC=3，AB=5，求AE的长．

查看试题解析
21. 某校为了解七、八年级学生对“新冠疫情”防护知识的掌握情况，从七、八年级各随机抽取30名学生进行测试，并对成绩（百分制）进行整理、描述和分析．部分信息如下：
①七年级成绩频数分布直方图（每组含最小值，不含最大值，最后一组含100分）；

②七年级在 $70 \leq x < 80$ 这一组的成绩是：78，74，76，78，77，79；

③七、八年级抽取学生成绩的平均数、中位数如下：

年级

平均数

中位数

七

74.8

$a$

八

75.4

78.5

根据以上信息，回答下列问题：

(1)、在这次测试中，七年级在70分以上（含70分）的有人；表中a的值为；

(2)、求七年级成绩在 $70 \leq x < 80$ 这一组的6个人成绩的方差；

(3)、参加测试的七年级小静同学说：“我和八年级的小蓓都是77分，但我在七年级抽取的同学中排名更靠前．”八年级小蓓同学说：“虽然我不知道其他人的分数，但我的分数是77分，比平均分高，所以我的成绩一定是八年级抽取同学中的前15名．”请你对这两种说法是否符合题意进行判断，并加以说明．

查看试题解析
22. 如图，抛物线y＝﹣（x﹣m）²+3的顶点A在第一象限，点B(m﹣3，0)在x轴的负半轴上，直线AB与y轴交于点C ，与抛物线的另一个交点P(h ， n)也在第一象限内．

(1)、若交点P(h ， n)是AC的中点，且h＝1，求n的值；

(2)、连接OP ，令 $△$ OCP面积为S ，求关于m的函数表达式（要求写出m的取值范围），并求出S的最大值．

查看试题解析
23. 如图，在矩形 $A B C D$ 中， $R t Δ B E C$ 的直角顶点E在边 $A D$ 上， $∠ C B E$ 的平分线 $B F$ 交 $C E$ 于点G，交边 $C D$ 于点F．

(1)、若点E为 $A D$ 中点，求证： $Δ A E B ≅ Δ D E C$ ；

(2)、若 $\sin ∠ B C E = \frac{4}{5}$ ，求证： $B G = 4 F G$ ；

(3)、若 $C F = 2 D F = 2$ ，求 $C E \cdot E G$ 的值．

查看试题解析

年级	平均数	中位数
七	74.8	$a$
八	75.4	78.5