初中数学苏科版2020-2021学年八年级下学期期末模拟试卷

试卷更新日期：2021-06-04 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式： $\frac{x}{2}$ ， $\frac{3}{x - 5}$ ，0， $- a^{2}$ ， $\frac{4}{3} x y^{2}$ ， $\frac{1}{b}$ ， $\frac{m}{π - 2}$ 中，是分式的有（）

A、1个 B、2个 C、3个 D、4 个

查看试题解析
2. 若1＜x＜3，则|x﹣3|+ $\sqrt{{(x - 1)}^{2}}$ 的值为（　　）

A、2x﹣4 B、-2 C、4﹣2x D、2

查看试题解析
3. 已知a= $\sqrt{2}$ ， b= $\sqrt{10}$ ，用含a、b的代数式表示 $\sqrt{20}$ ，这个代数式是（）

A、a+b B、ab C、2a D、2b

查看试题解析
4.
如图，菱形ABCD的两条对角线相交于O，若AC=6，BD=4，则菱形的周长是（　　）

A、24 B、16 C、4 $\sqrt{13}$ D、2 $\sqrt{3}$

查看试题解析
5. 在正方形 ABCD 中， P 为 AB 的中点， $B E ⊥ P D$ 的延长线于点 E ，连接 AE 、 BE ， $F A ⊥ A E$ 交 DP 于点 F ，连接 BF 、FC ，下列结论：① $△ A B E ≅ △ A D F$ ；② FB = AB ；③ $C F ⊥ P D$ ；④ FC = EF . 其中正确的是（）

A、①②④ B、①③④ C、①②③ D、①②③④

查看试题解析
6. 如图，在 $△ A B C$ 中，已知 $∠ C = 90 °$ ， $A C = B C = 4$ ， $D$ 是 $A B$ 的中点，点 $E$ 、 $F$ 分别在 $A C$ 、 $B C$ 边上运动（点 $E$ 不与点 $A$ 、 $C$ 重合），且保持 $A E = C F$ ，连接 $D E$ 、 $D F$ 、 $E F$ ．在此运动变化的过程中，有下列结论，其中正确的结论是（）
①四边形 $C E D F$ 有可能成为正方形；② $△ D F E$ 是等腰直角三角形；③四边形 $C E D F$ 的面积是定值；④点 $C$ 到线段 $E F$ 的最大距离为 $\sqrt{2}$ ．

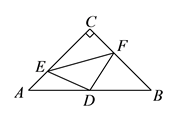A、①④ B、①②③ C、①②④ D、①②③④

查看试题解析
7. 若关于x的方程 =0没有增根，则m的值不能是（　　）

A、3 B、2 C、1 D、
−1

查看试题解析
8. 如图，在等腰△ABC中， $∠ A C B = 90^{°}$ ， $A C = 8$ ，F是AB边上的中点，点D，E分别在AC，BC边上运动，且保持 $A D = C E$ ，连接DE，DF，EF在此运动变化的过程中，下列结论：（1） $△ D E F$ 是等腰直角三角形； $(2)$ 四边形CDFE不可能为正方形，（3） $D E$ 长度的最小值为4；（4）连接CF，CF恰好把四边形CDFE的面积分成1：2两部分，则 $C E =$ $\frac{1}{3}$ 或 $\frac{14}{3}$ 其中正确的结论个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

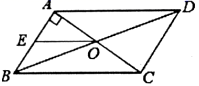
9. 二次根式 $\sqrt{\frac{1}{2 x - 1}}$ 中字母x的取值范围是．

查看试题解析
10. 如图， $▱ A B C D$ 的对角线AC与BD相交于点O， $A B ⊥ A C$ ，若AB=4，BD=10，点E是AB边的中点，则OE的长是.

查看试题解析
11. 已知关于x的方程 $\frac{m}{x - 1} = 1$ 的解是正数，m的范围是

查看试题解析
12. 如图，在矩形 $A B C D$ 中，点E为边 $A D$ 上一点，连接 $B E$ ，作 $∠ E B C$ 的平分线，交 $C D$ 于点F，连接 $E F$ ，若 $C F = 4$ ， $D F = 2$ ，且 $∠ E F B = 45 °$ ，则 $B E =$ .

查看试题解析
13. 已知x₁= $\sqrt{3}$ + $\sqrt{2}$ ，x₂= $\sqrt{3}$ ﹣ $\sqrt{2}$ ，则x₁²+x₂²= ．

查看试题解析
14. 如图，正方形ABCD对角线相交于点O，CP⊥DP于P，CP＝5，DP＝7，则△POD面积为.

查看试题解析

三、计算题

15. 解方程： $\frac{2}{1 + x} - \frac{3}{1 - x} = \frac{6}{x^{2} - 1}$

查看试题解析
16. 计算：

(1)、 $\sqrt{8} - \sqrt{32}$ ；

(2)、 ${(\sqrt{5} - 2)}^{2021} {(\sqrt{5} + 2)}^{2020}$ ；

(3)、 ${(2 \sqrt{3} - \sqrt{2})}^{2}$ ；

(4)、 $\sqrt{\frac{2}{3}} \times \sqrt{\frac{27}{8}} + 3 \sqrt{\frac{1}{3}} - {(\sqrt{3} - 2)}^{0}$ ．

查看试题解析
17. 已知 $a + b = 2 \sqrt{5}$ ， $a b = 1$ ，求 $\sqrt{\frac{b}{a} + \frac{a}{b}}$ 的值.

查看试题解析
18. 已知关于x的方程 $\frac{x^{2} + 4}{x (x - 2)} - \frac{x}{x - 2} = \frac{a}{x}$ 无解,求a的值.

查看试题解析

四、作图题

19. 如图，在建立平面直角坐标系的网格纸中，每个小方格都是边长为1个单位长度的小正方形，△ABC的顶点均在格点上，点P的坐标为（-1，0）．

(1)、把△ABC绕点P旋转180°得到△A’B’C’ ，作出△A’B’C’；

(2)、把△ABC向右平移7个单位长度得到△A″B″C″，作出△A″B″C″；

(3)、△A’B’C’与△A″B″C″是否成中心对称？若是，则找出对称中心P’ ，并写出其坐标；若不是，请说明理由．

查看试题解析
20. 如图，平行四边形ABCD中，点E为AB边上一点，请你用无刻度的直尺，在CD边上画出点 F，使四边形AECF为平行四边形，并说明理由．

查看试题解析
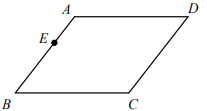21. 已知∠MAN，按要求完成下列尺规作图（不写作法，保留作图痕迹）：

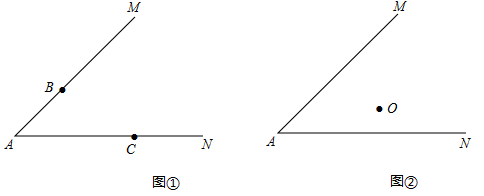(1)、如图①，B、C分别在射线AM、AN上，求作▱ABDC；

(2)、如图②，点O是∠MAN内一点，求作线段PQ，使P、Q分别在射线AM、AN上，且点O是PQ的中点.

查看试题解析
22. 如下是小东设计的“作平行四边形一边中点”的尺规作图过程.
已知：平行四边形 $A B C D$ .

求作：点 $M$ ，使点 $M$ 为边 $A D$ 的中点.

作法：如图，

①作射线 $B A$ ；

②以点 $A$ 为圆心， $C D$ 长为半径画弧，

交 $B A$ 的延长线于点 $E$ ；

③连接 $E C$ 交 $A D$ 于点 $M$ .

所以点 $M$ 就是所求作的点.

根据小东设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、完成下面的证明.
证明：连接 $A C$ ， $E D$ .

$∵$ 四边形 $A B C D$ 是平行四边形，

$∴ A E / / C D$ .

$∵ A E =$ ▲ ，

$∴$ 四边形 $E A C D$ 是平行四边形 $($ ▲ $)$ （填推理的依据）.

$∴ A M = M D ($ ▲ $)$ （填推理的依据）.

$∴$ 点 $M$ 为所求作的边 $A D$ 的中点.

查看试题解析

五、综合题

23. 随着科技的进步和网络资源的丰富，在线学习已成为更多人的自主学习选择，某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论，为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如下两幅不完整的统计图.

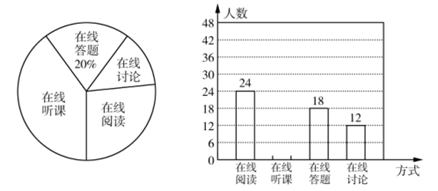
根据图中信息，解答下列问题：

(1)、求本次调查的学生总人数，并通过计算补全条形统计图；

(2)、求扇形统计图中“在线讨论”对应的扇形圆心角的度数；

(3)、该校共有学生1800人，请你估计该校对在线阅读最感兴趣的学生人数.

查看试题解析
24. 如图：在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线交BC于点E（尺规作图的痕迹保留在图中了），连接EF.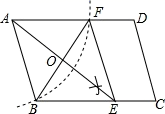

(1)、求证：四边形ABEF为菱形；

(2)、AE，BF相交于点O，若BF＝6，AB＝5，求AE的长.

查看试题解析
25. 已知矩形的面积为1，设该矩形的长为x，周长为y，小彬借鉴以前研究函数的经验，对函数y随自变量x的变化进行了探究；以下是小彬的探究过程：

(1)、结合问题情境分析：
①y与x的函数表达式为；②自变量x的取值范围是．

(2)、下表是y与x的几组对应值．
x
…
$\frac{1}{4}$
$\frac{1}{3}$
$\frac{1}{2}$
1
2
3
4
…
y
…
$\frac{17}{2}$
$\frac{20}{3}$
5
4
m
$\frac{20}{3}$
$\frac{17}{2}$
…
①写出m的值；
②画出函数图象；
③观察图象，写出该函数两条不同类型的性质．

查看试题解析
26.
如图，在平面直角坐标系中，正比例函数y=kx（k>0）与反比例函数y= $\frac{3}{x}$ 的图象分别交于A、C两点，已知点B与点D关于坐标原点O成中心对称，且点B的坐标为（m ， 0）．其中m>0．

(1)、四边形ABCD的是． (填写四边形ABCD的形状)

(2)、当点A的坐标为（n ， 3）时，四边形ABCD是矩形，求mn的值．

(3)、试探究：随着k与m的变化，四边形ABCD能不能成为菱形？若能，请直接写出k的值；若不能，请说明理由．

查看试题解析
27. 【知识链接】连结三角形两边中点的线段，叫做三角形的中位线．
【动手操作】小明同学在探究证明中位线性质定理时，是沿着中位线将三角形剪开然后将它们无缝隙、无重叠的拼在一起构成平行四边形，从而得出：三角形中位线平行于第三边且等于第三边的一半．

【性质证明】小明为证明定理，他想利用三角形全等、平行四边形的性质来证明．请你帮他完成解题过程（要求：画出图形，根据图形写出已知、求证和证明过程）．

查看试题解析
28. 在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点．过点A作AF∥BC交BE的延长线于点F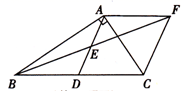

(1)、求证：△AEF≌△DEB；

(2)、证明四边形ADCF是菱形；

(3)、若AC=4，AB=5，求菱形ADCFD 的面积．

查看试题解析
29. A、B两地相距18千米，甲工程队要在A、B两地间铺设一条输送天然气的管道，乙工程队要在A、B两地间铺设一条输油管道，已知甲工程队每天比乙工程队少铺设1千米．

(1)、若两队同时开工，甲工程队每天铺设3千米，求乙工程队比甲工程队提前几天完成？

(2)、若甲工程队提前3天开工，结果两队同时完成任务，求甲、乙两队每天各铺设管道多少千米？

查看试题解析
30. 如图，已知，A（0，4），B（﹣3，0），C（2，0），D为B点关于AC的对称点，反比例函数y＝ $\frac{k}{x}$ 的图象经过D点．

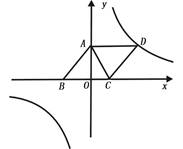(1)、证明：四边形ABCD为菱形；

(2)、求此反比例函数的解析式；

(3)、设过点C和点D的一次函数y＝kx+b，求不等式kx+b﹣ $\frac{k}{x}$ ＞0的解．（请直接写出当 $x > 0$ 时的答案）；

(4)、已知在y＝ $\frac{k}{x}$ 的图象上一点N，y轴上一点M，且点A、B、M、N组成四边形是平行四边形，求M点的坐标．

查看试题解析

x	…	$\frac{1}{4}$	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	4	…
y	…	$\frac{17}{2}$	$\frac{20}{3}$	5	4	m	$\frac{20}{3}$	$\frac{17}{2}$	…