湘教版备考2021年中考数学三轮复习专题12 几何变换问题
试卷更新日期:2021-06-04 类型:三轮冲刺
一、单选题
-
1. 如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
 A、(﹣4,﹣2﹣ ) B、(﹣4,﹣2+ ) C、(﹣2,﹣2+ ) D、(﹣2,﹣2﹣ )2. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A、(﹣4,﹣2﹣ ) B、(﹣4,﹣2+ ) C、(﹣2,﹣2+ ) D、(﹣2,﹣2﹣ )2. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( ) A、(4n﹣1,) B、(2n﹣1,) C、(4n+1,) D、(2n+1,)3. 如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( )
A、(4n﹣1,) B、(2n﹣1,) C、(4n+1,) D、(2n+1,)3. 如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( ) A、(4.8,6.4) B、(4,6) C、(5.4,5.8) D、(5,6)4. 如图,已知点D,E是 的三等分点, , 将 分成三部分,且 ,图中三部分的面积分别为 , , ,则 的值为( )
A、(4.8,6.4) B、(4,6) C、(5.4,5.8) D、(5,6)4. 如图,已知点D,E是 的三等分点, , 将 分成三部分,且 ,图中三部分的面积分别为 , , ,则 的值为( ) A、 B、 C、 D、5. 如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(2,4).点A在 轴的正半轴上,点C在 轴的正半轴上,点P是BC的中点.以坐标原点O为位似中心,将矩形OABC放大为原图形的1.5倍,记点P的对应点为P1 , 则P1的坐标为( )
A、 B、 C、 D、5. 如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(2,4).点A在 轴的正半轴上,点C在 轴的正半轴上,点P是BC的中点.以坐标原点O为位似中心,将矩形OABC放大为原图形的1.5倍,记点P的对应点为P1 , 则P1的坐标为( )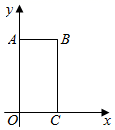 A、(3,3) B、(3,2)或( , ) C、(3,3)或( , ) D、(2,3)或( , )6. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标( )
A、(3,3) B、(3,2)或( , ) C、(3,3)或( , ) D、(2,3)或( , )6. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标( )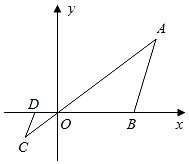 A、(﹣1,﹣1) B、(﹣ ,﹣1) C、(﹣1,﹣ ) D、(﹣2,﹣1)7. 如图,在三角形ABC中,M,N分别是边AB,AC上的点,AM= AB,AN= AC,则三角形AMN的面积与四边形MBCN的面积比( )
A、(﹣1,﹣1) B、(﹣ ,﹣1) C、(﹣1,﹣ ) D、(﹣2,﹣1)7. 如图,在三角形ABC中,M,N分别是边AB,AC上的点,AM= AB,AN= AC,则三角形AMN的面积与四边形MBCN的面积比( )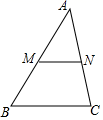 A、 B、 C、 D、8. 如图,已知 和 是以点O为位似中心的位似图形,且 和 的周长之比为 ,点B的坐标为 ,则点 的坐标为( ).
A、 B、 C、 D、8. 如图,已知 和 是以点O为位似中心的位似图形,且 和 的周长之比为 ,点B的坐标为 ,则点 的坐标为( ). A、 B、 C、 D、9. 如图,以点O为位似中心,将 放大得到 ,若 的面积为4,则 的面积为( )
A、 B、 C、 D、9. 如图,以点O为位似中心,将 放大得到 ,若 的面积为4,则 的面积为( ) A、2 B、8 C、16 D、2410. 如图,四边形ABCD和四边形A'B'C'D'是以点O为位似中心的位似图形,若OA:OA'=3:5,则四边形ABCD和四边形A'B'C'D'的面积比为( )
A、2 B、8 C、16 D、2410. 如图,四边形ABCD和四边形A'B'C'D'是以点O为位似中心的位似图形,若OA:OA'=3:5,则四边形ABCD和四边形A'B'C'D'的面积比为( )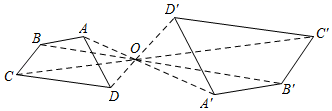 A、3:5 B、3:8 C、9:25 D、 :
A、3:5 B、3:8 C、9:25 D、 :二、填空题
-
11. 如图,点O是△ABC内一点,分别连接OA、OB、OC并延长到点D、E、F,使AD=2OA,BE=2OB,CF=2OC,连接DE,EF,FD,若△ABC的面积是3,则阴影部分的面积是.
 12. 在平面直角坐标系中,Rt△OAB的顶点A的坐标为( ,1),若将△OAB绕O点,逆时针旋转60°后,B点到达B′点,则点B′的坐标是.
12. 在平面直角坐标系中,Rt△OAB的顶点A的坐标为( ,1),若将△OAB绕O点,逆时针旋转60°后,B点到达B′点,则点B′的坐标是.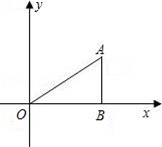 13. 如图,D是 的边BC上一点, , , .如果 的面积为15,那么 的面积为.
13. 如图,D是 的边BC上一点, , , .如果 的面积为15,那么 的面积为.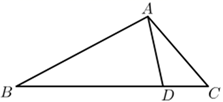 14. 在直角△ABC中,∠C=90°,CD⊥AB,由∽ , 可得AC2=AD·AB.
14. 在直角△ABC中,∠C=90°,CD⊥AB,由∽ , 可得AC2=AD·AB. 15. 如图,在矩形 中, ,点 分别是 上的两点,连接 ,将矩形 沿 折叠,使点 恰好落在 边上的中点 处,连接 则折痕 的长为 .
15. 如图,在矩形 中, ,点 分别是 上的两点,连接 ,将矩形 沿 折叠,使点 恰好落在 边上的中点 处,连接 则折痕 的长为 . 16. 如图, ,点 在 上, 与 交于点 , , ,则 的长为 .
16. 如图, ,点 在 上, 与 交于点 , , ,则 的长为 .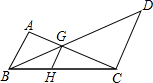 17. 如图,在 中, , ,延长 至点 ,使 ,则 .
17. 如图,在 中, , ,延长 至点 ,使 ,则 . 18. 如图,在 中, , CD是斜边AB上的高.下列结论①CD2=AD·BD ②AC2=AD·AB ③BC2=AB·BD④BD2=AC·BC错误的是
18. 如图,在 中, , CD是斜边AB上的高.下列结论①CD2=AD·BD ②AC2=AD·AB ③BC2=AB·BD④BD2=AC·BC错误的是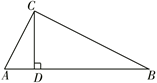 19. 如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若PA= ,则PB+PC= .
19. 如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若PA= ,则PB+PC= . 20. 如图,△ABC中,∠C=90°,AC=6,BC=4,点O是AC的中点,以O为旋转中心,将△ABC绕点O旋转一周,A、B、C的对应点分别为A'、B'、C',则BC'的最大值为 .
20. 如图,△ABC中,∠C=90°,AC=6,BC=4,点O是AC的中点,以O为旋转中心,将△ABC绕点O旋转一周,A、B、C的对应点分别为A'、B'、C',则BC'的最大值为 .
三、作图题
-
21. 如图,两个任意四边形中心对称,请找出它们的对称中心.
 22. 每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.
22. 每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上. (1)、把△ABC向上平移5个单位后得到对应的△A1B1C1 , 画出△A1B1C1;(2)、画出与△ABC关于原点O对称的△A2B2C2;(3)、△A1B1C1与△A2B2C2关于某个点对称,则这个点的坐标为 .23. 如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,﹣2).
(1)、把△ABC向上平移5个单位后得到对应的△A1B1C1 , 画出△A1B1C1;(2)、画出与△ABC关于原点O对称的△A2B2C2;(3)、△A1B1C1与△A2B2C2关于某个点对称,则这个点的坐标为 .23. 如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,﹣2). (1)、以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 , 使它与△OAB的相似比为2:1,并写出点A的对应点A1的坐标;(2)、画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2 , 并写出点A2的坐标;(3)、判断△OA1B1与△O2A2B2 , 能否是关于某一点M为位似中心的位似图形?若是,请在图中标出位似中心M,并写出点M的坐标.
(1)、以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 , 使它与△OAB的相似比为2:1,并写出点A的对应点A1的坐标;(2)、画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2 , 并写出点A2的坐标;(3)、判断△OA1B1与△O2A2B2 , 能否是关于某一点M为位似中心的位似图形?若是,请在图中标出位似中心M,并写出点M的坐标.四、综合题
-
24. 已知点O是正方形ABCD对角线BD的中点.(1)、如图1,若点E是OD的中点,点F是AB上一点,且使得∠CEF=90°,过点E作ME∥AD,交AB于点M,交CD于点N.

①∠AEM=∠FEM; ②点F是AB的中点;
(2)、如图2,若点E是OD上一点,点F是AB上一点,且使 = = ,请判断△EFC的形状,并说明理由;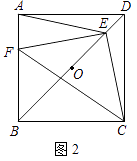 (3)、如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当 = 时,请猜想 的值(请直接写出结论).
(3)、如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当 = 时,请猜想 的值(请直接写出结论). 25. 如图,在▱ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
25. 如图,在▱ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.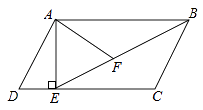 (1)、求证:△ABF∽△BEC;(2)、若AD=5,AB=8,sinD= ,求AF的长.26. 解答题(1)、将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是 , ∠CAC′=°.
(1)、求证:△ABF∽△BEC;(2)、若AD=5,AB=8,sinD= ,求AF的长.26. 解答题(1)、将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是 , ∠CAC′=°. (2)、如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.
(2)、如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论. (3)、如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,说明理由.
(3)、如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,说明理由. 27. 我们给出如下定义:若一个四边形有一组对角互补(即对角之和为180°),则称这个四边形为圆满四边形.(1)、概念理解:在平行四边形、菱形、矩形、正方形中,你认为属于圆满四边形的有 .(2)、问题探究:如图,在四边形ABCD中,对角线AC、BD相交于点O,若∠ADB=∠ACB,问四边形ABCD是圆满四边形吗?请说明理由.小明经过思考后,判断四边形ABCD是圆满四边形,并提出了如下探究思路:先证明△AOD∽△BOC,得到比例式 = ,再证明△AOB∽△DOC,得出对应角相等,根据四边形内角和定理,得出一组对角互补.请你帮助小明写出解题过程.
27. 我们给出如下定义:若一个四边形有一组对角互补(即对角之和为180°),则称这个四边形为圆满四边形.(1)、概念理解:在平行四边形、菱形、矩形、正方形中,你认为属于圆满四边形的有 .(2)、问题探究:如图,在四边形ABCD中,对角线AC、BD相交于点O,若∠ADB=∠ACB,问四边形ABCD是圆满四边形吗?请说明理由.小明经过思考后,判断四边形ABCD是圆满四边形,并提出了如下探究思路:先证明△AOD∽△BOC,得到比例式 = ,再证明△AOB∽△DOC,得出对应角相等,根据四边形内角和定理,得出一组对角互补.请你帮助小明写出解题过程. (3)、问题解决:请结合上述解题中所积累的经验和知识完成下题.如图,四边形ABCD中,AD⊥BD,AC⊥BC,AB与DC的延长线相交于点E,BE=BD,AB=5,AD=3,求CE的长.
(3)、问题解决:请结合上述解题中所积累的经验和知识完成下题.如图,四边形ABCD中,AD⊥BD,AC⊥BC,AB与DC的延长线相交于点E,BE=BD,AB=5,AD=3,求CE的长.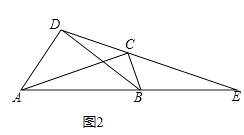 28. 在△ABC中,CA=CB,在△AED中,DA=DE,点D,E分别在CA,AB上.(1)、如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是;
28. 在△ABC中,CA=CB,在△AED中,DA=DE,点D,E分别在CA,AB上.(1)、如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是;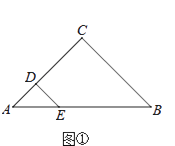 (2)、若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,则CD与BE的数量关系是;,
(2)、若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,则CD与BE的数量关系是;, (3)、若∠ACB=∠ADE=2α(0°<α<90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示).
(3)、若∠ACB=∠ADE=2α(0°<α<90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示). 29. 【问题提出】如图①,已知海岛A到海岸公路BD的距离为AB,C为公路BD上的酒店,从海岛A到酒店C,先乘船到登陆点D,船速为a,再乘汽车,车速为船速的n倍,点D选在何处时,所用时间最短?
29. 【问题提出】如图①,已知海岛A到海岸公路BD的距离为AB,C为公路BD上的酒店,从海岛A到酒店C,先乘船到登陆点D,船速为a,再乘汽车,车速为船速的n倍,点D选在何处时,所用时间最短?【特例分析】若n=2,则时间t= + ,当a为定值时,问题转化为:在BC上确定一点D,使得AD+ 的值最小.如图②,过点C做射线CM,使得∠BCM=30°.
 (1)、过点D作DE⊥CM,垂足为E,试说明:DE= ;(2)、【问题解决】请在图②中画出所用时间最短的登陆点D′,并说明理由.(3)、【模型运用】请你仿照“特例分析”中的相关步骤,解决图①中的问题(写出具体方案,如相关图形呈现、图形中角所满足的条件、作图的方法等).
(1)、过点D作DE⊥CM,垂足为E,试说明:DE= ;(2)、【问题解决】请在图②中画出所用时间最短的登陆点D′,并说明理由.(3)、【模型运用】请你仿照“特例分析”中的相关步骤,解决图①中的问题(写出具体方案,如相关图形呈现、图形中角所满足的条件、作图的方法等).
(4)、如图③,海面上一标志A到海岸BC的距离AB=300m,BC=300m.救生员在C点处发现标志A处有人求救,立刻前去营救,若救生员在岸上跑的速度都是6m/s,在海中游泳的速度都是2m/s,求救生员从C点出发到
达A处的最短时间.
30. 如图1,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC. (1)、求证:BD=EC.(2)、探究线段BD,DC,AD之间的数量关系并说明理由.(3)、如图2,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=8,CD=4,求AD的长.
(1)、求证:BD=EC.(2)、探究线段BD,DC,AD之间的数量关系并说明理由.(3)、如图2,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=8,CD=4,求AD的长.