湘教版备考2021年中考数学三轮复习专题13 动点变换问题
试卷更新日期:2021-06-04 类型:三轮冲刺
一、单选题
-
1. 已知点 和直线 ,求点P到直线 的距离d可用公式 计算.根据以上材料解决下面问题:如图, 的圆心C的坐标为 ,半径为1,直线l的表达式为 ,P是直线l上的动点,Q是 上的动点,则 的最小值是( )
 A、 B、 C、 D、22. 如图,平行于y轴的直线分别交 与 的图象(部分)于点A、B,点C是y轴上的动点,则 的面积为( )
A、 B、 C、 D、22. 如图,平行于y轴的直线分别交 与 的图象(部分)于点A、B,点C是y轴上的动点,则 的面积为( ) A、 B、 C、 D、3. 如图,点A(a , 1),B(b , 3)都在双曲线y=﹣ 上,点P , Q分别是x轴,y轴上的动点,则四边形ABPQ周长的最小值为( )
A、 B、 C、 D、3. 如图,点A(a , 1),B(b , 3)都在双曲线y=﹣ 上,点P , Q分别是x轴,y轴上的动点,则四边形ABPQ周长的最小值为( )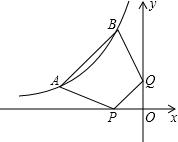 A、4 B、6 C、2 +2 D、84. 如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数 上一个动点, 轴于点B , 当点P的横坐标逐渐增大时,四边形OAPB的面积将会
A、4 B、6 C、2 +2 D、84. 如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数 上一个动点, 轴于点B , 当点P的横坐标逐渐增大时,四边形OAPB的面积将会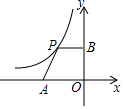 A、先增后减 B、先减后增 C、逐渐减小 D、逐渐增大5. 如图,在菱形ABCD中,∠A=60°,AD=4,点P是AB边上的一个动点,点E、F分别是DP、BP的中点,则线段EF的长为( )
A、先增后减 B、先减后增 C、逐渐减小 D、逐渐增大5. 如图,在菱形ABCD中,∠A=60°,AD=4,点P是AB边上的一个动点,点E、F分别是DP、BP的中点,则线段EF的长为( )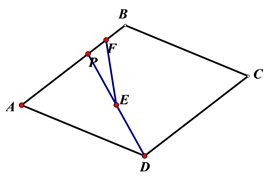 A、2 B、4 C、 D、6. 如图,在矩形ABCD中,AB=6,BC=10,P是AD边上一动点(不含端点A,D),连接PC,E是AB边上一点,设BE=a,若存在唯一点P,使∠EPC=90°,则a的值是( )
A、2 B、4 C、 D、6. 如图,在矩形ABCD中,AB=6,BC=10,P是AD边上一动点(不含端点A,D),连接PC,E是AB边上一点,设BE=a,若存在唯一点P,使∠EPC=90°,则a的值是( )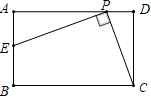 A、 B、 C、3 D、67. 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧 上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )
A、 B、 C、3 D、67. 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧 上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )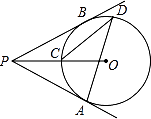 A、15° B、20° C、25° D、30°8. 已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如右图所示,则该封闭图形可能是 ( )
A、15° B、20° C、25° D、30°8. 已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如右图所示,则该封闭图形可能是 ( )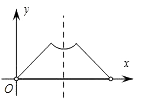 A、
A、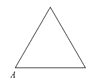 B、
B、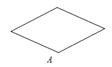 C、
C、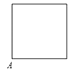 D、
D、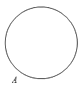 9. 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=6cm,动点P从点C沿CA,以1cm/s的速度向点A运动,同时动点O从点C沿CB,以2cm/s的速度向点B运动,其中一个动点到达终点时,另一个动点也停止运动.则运动过程中所构成的△CPO的面积y(cm2)与运动时间x(s)之间的函数图象大致是( )
9. 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=6cm,动点P从点C沿CA,以1cm/s的速度向点A运动,同时动点O从点C沿CB,以2cm/s的速度向点B运动,其中一个动点到达终点时,另一个动点也停止运动.则运动过程中所构成的△CPO的面积y(cm2)与运动时间x(s)之间的函数图象大致是( )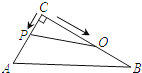 A、
A、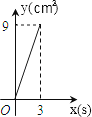 B、
B、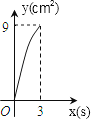 C、
C、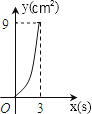 D、
D、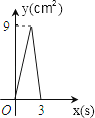 10.
10.如图,在Rt△ABC中,∠A=90°,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值大小变化情况是( )
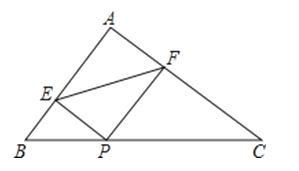 A、一直增大 B、一直减小 C、先减小后增大 D、先增大后减少
A、一直增大 B、一直减小 C、先减小后增大 D、先增大后减少二、填空题
-
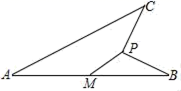
11. 如图,线段AB=4,M为AB的中点,动点P到点M的距离是1,连接PB,线段PB绕点P逆时针旋转90°得到线段PC,连接AC,则线段AC长度的最大值是 .
 12. 如图,抛物线 的图象与坐标轴交于点A , B , D , 顶点为E , 以AB为直径画半圆交y正半轴交于点C , 圆心为M , P是半圆上的一动点,连接EP . ①点E在⊙M的内部;②CD的长为 ;③若P与C重合,则∠DPE=15°;④在P的运动过程中,若AP= ,则PE= ⑤N是PE的中点,当P沿半圆从点A运动至点B时,点N运动的路径长是2π.其中结论正确的是
12. 如图,抛物线 的图象与坐标轴交于点A , B , D , 顶点为E , 以AB为直径画半圆交y正半轴交于点C , 圆心为M , P是半圆上的一动点,连接EP . ①点E在⊙M的内部;②CD的长为 ;③若P与C重合,则∠DPE=15°;④在P的运动过程中,若AP= ,则PE= ⑤N是PE的中点,当P沿半圆从点A运动至点B时,点N运动的路径长是2π.其中结论正确的是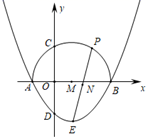 13. 如图,函数 (k为常数,k>0)的图象与过原点的O的直线相交于A , B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线AM分别交x轴,y轴于C , D两点,连接BM分别交x轴,y轴于点E , F . 现有以下四个结论:①△ODM与△OCA的面积相等;②若BM⊥AM于点M , 则∠MBA=30°;③若M点的横坐标为1,△OAM为等边三角形,则 ;④若 ,则MD=2MA . 其中正确的结论的序号是 .
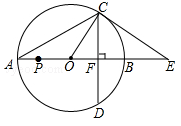
13. 如图,函数 (k为常数,k>0)的图象与过原点的O的直线相交于A , B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线AM分别交x轴,y轴于C , D两点,连接BM分别交x轴,y轴于点E , F . 现有以下四个结论:①△ODM与△OCA的面积相等;②若BM⊥AM于点M , 则∠MBA=30°;③若M点的横坐标为1,△OAM为等边三角形,则 ;④若 ,则MD=2MA . 其中正确的结论的序号是 .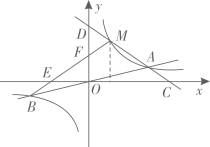 14. 如图,以AB为直径的⊙O与CE相切于点C , CE交AB的延长线于点E , 直径AB=18,∠A=30°,弦CD⊥AB , 垂足为点F , 连接AC , OC , 则下列结论正确的是 . (写出所有符合题意结论的序号)
14. 如图,以AB为直径的⊙O与CE相切于点C , CE交AB的延长线于点E , 直径AB=18,∠A=30°,弦CD⊥AB , 垂足为点F , 连接AC , OC , 则下列结论正确的是 . (写出所有符合题意结论的序号)① ;
②扇形OBC的面积为 π;
③△OCF∽△OEC;
④若点P为线段OA上一动点,则AP•OP有最大值20.25.
 15. 如图, 是锐角 的外接圆, 是 的切线,切点为F, ,连结 交 于E, 的平分线 交 于D,连结 .下列结论:① 平分 ;②连接 ,点F为 的外心;③ ;④若点M,N分别是 和 上的动点,则 的最小值是 .其中一定正确的是(把你认为正确结论的序号都填上).
15. 如图, 是锐角 的外接圆, 是 的切线,切点为F, ,连结 交 于E, 的平分线 交 于D,连结 .下列结论:① 平分 ;②连接 ,点F为 的外心;③ ;④若点M,N分别是 和 上的动点,则 的最小值是 .其中一定正确的是(把你认为正确结论的序号都填上).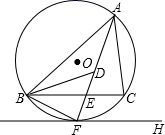 16. 如图,在直角坐标系中,正方形ABCO的点B坐标(3,3),点A、C分别在y轴、x轴上,对角线AC上一动点E,连接BE,过E作DE⊥BE交OC于点D.若点D坐标为(2,0),则点E坐标为 .
16. 如图,在直角坐标系中,正方形ABCO的点B坐标(3,3),点A、C分别在y轴、x轴上,对角线AC上一动点E,连接BE,过E作DE⊥BE交OC于点D.若点D坐标为(2,0),则点E坐标为 .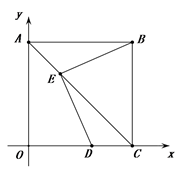 17. 如图,⊙O是锐角△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.下列结论:①AF平分∠BAC;②点F为△BDC的外心;③ ;④若点M,N分别是AB和AF上的动点,则BN+MN的最小值是ABsin∠BAC.其中一定正确的是(把你认为正确结论的序号都填上).
17. 如图,⊙O是锐角△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.下列结论:①AF平分∠BAC;②点F为△BDC的外心;③ ;④若点M,N分别是AB和AF上的动点,则BN+MN的最小值是ABsin∠BAC.其中一定正确的是(把你认为正确结论的序号都填上).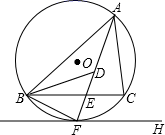 18. 如图,边长为1的正△ABO的顶点O在原点,点B在x轴负半轴上,正方形OEDC边长为2,点C在y轴正半轴上,动点P从点A出发,以每秒1个单位的速度沿着△ABO的边按逆时针方向运动,动点Q从D点出发,以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动,点Q比点P迟1秒出发,则点P运动2016秒后,则PQ2的值是 .
18. 如图,边长为1的正△ABO的顶点O在原点,点B在x轴负半轴上,正方形OEDC边长为2,点C在y轴正半轴上,动点P从点A出发,以每秒1个单位的速度沿着△ABO的边按逆时针方向运动,动点Q从D点出发,以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动,点Q比点P迟1秒出发,则点P运动2016秒后,则PQ2的值是 .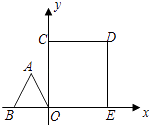 19. 如图,在Rt△ABC中,∠A=90°, ∠B=30°,BC= +1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为 .
19. 如图,在Rt△ABC中,∠A=90°, ∠B=30°,BC= +1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为 .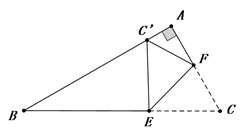 20. 如图, 为等边△ABC的外接圆,半径为2,点D在劣弧 上运动(不与点A,B重合),连接DA,DB,DC.则四边形ADBC的面积的最大值为 .
20. 如图, 为等边△ABC的外接圆,半径为2,点D在劣弧 上运动(不与点A,B重合),连接DA,DB,DC.则四边形ADBC的面积的最大值为 .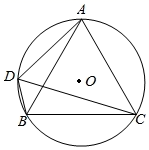
三、作图题
-
21. 若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.
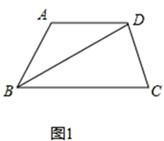
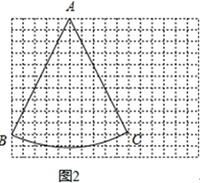 (1)、如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;(2)、如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;(3)、四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.
(1)、如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;(2)、如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;(3)、四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.四、综合题
-
22. 在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB向点B方向运动.如果点P的速度是2cm/秒,点Q的速度是1cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.
 (1)、用含t的代数式表示Rt△CPQ的面积S;(2)、当t=2秒时,P,Q两点之间的距离是多少?(3)、当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?23. 如图,在平面直角坐标系中,二次函数y=﹣ x2+bx+c的图象与y轴交于点A(0,8),与x轴交于B、C两点,其中点C的坐标为(4,0).点P(m,n)为该二次函数在第二象限内图象上的动点,点D的坐标为(0,4),连接BD.
(1)、用含t的代数式表示Rt△CPQ的面积S;(2)、当t=2秒时,P,Q两点之间的距离是多少?(3)、当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?23. 如图,在平面直角坐标系中,二次函数y=﹣ x2+bx+c的图象与y轴交于点A(0,8),与x轴交于B、C两点,其中点C的坐标为(4,0).点P(m,n)为该二次函数在第二象限内图象上的动点,点D的坐标为(0,4),连接BD.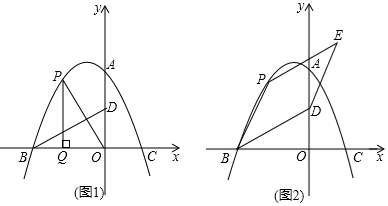 (1)、求该二次函数的表达式及点B的坐标;(2)、连接OP,过点P作PQ⊥x轴于点Q,当以O、P、Q为顶点的三角形与△OBD相似时,求m的值;(3)、连接BP,以BD、BP为邻边作▱BDEP,直线PE交y轴于点T.
(1)、求该二次函数的表达式及点B的坐标;(2)、连接OP,过点P作PQ⊥x轴于点Q,当以O、P、Q为顶点的三角形与△OBD相似时,求m的值;(3)、连接BP,以BD、BP为邻边作▱BDEP,直线PE交y轴于点T.①当点E落在该二次函数图象上时,求点E的坐标;
②在点P从点A到点B运动过程中(点P与点A不重合),直接写出点T运动的路径长.
24. 如图1,在等边 中, ,动点P从点A出发以 的速度沿 匀速运动,动点Q同时从点C出发以同样的速度沿 的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为 ,过点P作 于E, 交 边于D,线段 的中点为M,连接 .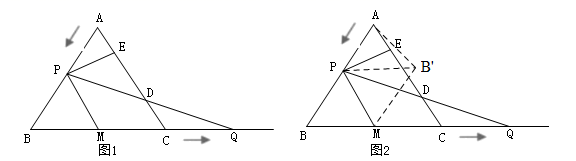 (1)、当t为何值时, 与 相似;(2)、在点P、Q运动过程中,点D、E也随之运动,线段 的长度是否会发生变化?若发生变化,请说明理由,若不发生变化,求 的长;(3)、如图2,将 沿直线 翻折,得 ,连接 ,当t为何值时, 的值最小?并求出最小值.25. 如图,已知二次函数 与x轴交于A、B两点(A点在B点左),与y轴交于C点,连接 ,点P为二次函数图象上的动点.
(1)、当t为何值时, 与 相似;(2)、在点P、Q运动过程中,点D、E也随之运动,线段 的长度是否会发生变化?若发生变化,请说明理由,若不发生变化,求 的长;(3)、如图2,将 沿直线 翻折,得 ,连接 ,当t为何值时, 的值最小?并求出最小值.25. 如图,已知二次函数 与x轴交于A、B两点(A点在B点左),与y轴交于C点,连接 ,点P为二次函数图象上的动点.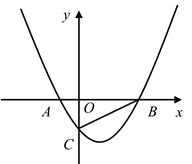
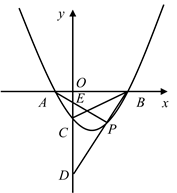 (1)、若 的面积为3,求抛物线的解析式;(2)、在(1)的条件下,若在y轴上存在点F,使得 ,求点P的坐标;(3)、若P为对称轴右侧抛物线上的动点,直线 交y轴于E点,直线 交y轴于点D,判断 的值是否为定值,若是,求出定值,若不是请说明理由.26. 如图,在平面直角坐标系中,矩形 的边 与x轴、y轴的交点分别为 ,抛物线 过B , C两点,动点M从点D开始以每秒5个单位长度的速度沿 的方向运动到达C点后停止运动.动点N从点O以每秒4个单位长度的速度沿 方向运动,到达C点后,立即返回,向 方向运动,到达O点后,又立即返回,依此在线段 上反复运动,当点M停止运动时,点N也停止运动,设运动时间为 .
(1)、若 的面积为3,求抛物线的解析式;(2)、在(1)的条件下,若在y轴上存在点F,使得 ,求点P的坐标;(3)、若P为对称轴右侧抛物线上的动点,直线 交y轴于E点,直线 交y轴于点D,判断 的值是否为定值,若是,求出定值,若不是请说明理由.26. 如图,在平面直角坐标系中,矩形 的边 与x轴、y轴的交点分别为 ,抛物线 过B , C两点,动点M从点D开始以每秒5个单位长度的速度沿 的方向运动到达C点后停止运动.动点N从点O以每秒4个单位长度的速度沿 方向运动,到达C点后,立即返回,向 方向运动,到达O点后,又立即返回,依此在线段 上反复运动,当点M停止运动时,点N也停止运动,设运动时间为 . (1)、求抛物线的解析式;(2)、求点D的坐标;(3)、当点M , N同时开始运动时,若以点M , D , C为顶点的三角形与以点B , O , N为顶点的三角形相似,求t的值;(4)、过点D与x轴平行的直线,交抛物线的对称轴于点Q , 将线段 沿过点B的直线翻折,点A的对称点为 ,求 的最小值.27. 如图,半径为4的 中,弦AB的长度为 ,点C是劣弧 上的一个动点,点D是弦AC的中点,点E是弦BC的中点,连接DE,OD,OE.
(1)、求抛物线的解析式;(2)、求点D的坐标;(3)、当点M , N同时开始运动时,若以点M , D , C为顶点的三角形与以点B , O , N为顶点的三角形相似,求t的值;(4)、过点D与x轴平行的直线,交抛物线的对称轴于点Q , 将线段 沿过点B的直线翻折,点A的对称点为 ,求 的最小值.27. 如图,半径为4的 中,弦AB的长度为 ,点C是劣弧 上的一个动点,点D是弦AC的中点,点E是弦BC的中点,连接DE,OD,OE.
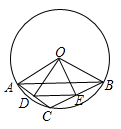 (1)、求 的度数;(2)、当点C沿着劣弧 从点A开始,逆时针运动到点B时,求 的外心P所经过的路径的长度;(3)、分别记 的面积为 ,当 时,求弦AC的长度.28. 如图,已知抛物线 经过点 ,与x轴交于 两点, 为顶点,P为抛物线上一动点(与点 不重合)
(1)、求 的度数;(2)、当点C沿着劣弧 从点A开始,逆时针运动到点B时,求 的外心P所经过的路径的长度;(3)、分别记 的面积为 ,当 时,求弦AC的长度.28. 如图,已知抛物线 经过点 ,与x轴交于 两点, 为顶点,P为抛物线上一动点(与点 不重合)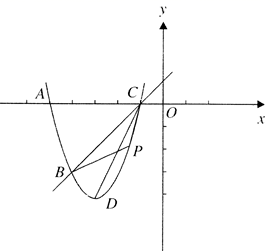 (1)、求该抛物线的解析式;(2)、当点 在直线 的下方运动时,求 的面积的最大值;(3)、该抛物线上是否存在点P,使 ?若存在,求出所有点P的坐标;若不存在,请说明理由.29. 如图, 中, , , ,动点 从点 出发,在 边上以每秒 的速度向点 匀速运动,同时动点 从点 出发,在 边上以每秒 的速度向点 匀速运动,运动时间为 秒( ),连接 .
(1)、求该抛物线的解析式;(2)、当点 在直线 的下方运动时,求 的面积的最大值;(3)、该抛物线上是否存在点P,使 ?若存在,求出所有点P的坐标;若不存在,请说明理由.29. 如图, 中, , , ,动点 从点 出发,在 边上以每秒 的速度向点 匀速运动,同时动点 从点 出发,在 边上以每秒 的速度向点 匀速运动,运动时间为 秒( ),连接 .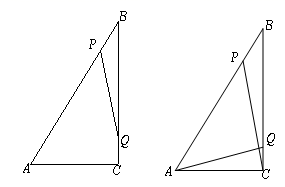 (1)、若 与 相似,求 的值;(2)、连接 , ,若 ,求 的值30. 已知直线 与抛物线 (b,c为常数, )的一个交点为 ,点 是x轴正半轴上的动点.(1)、当直线 与抛物线 (b,c为常数, )的另一个交点为该抛物线的顶点E时,求k,b,c的值及抛物线顶点E的坐标;(2)、在(1)的条件下,设该抛物线与y轴的交点为C,若点Q在抛物线上,且点Q的横坐标为b,当 时,求m的值;(3)、点D在抛物线上,且点D的横坐标为 ,当 的最小值多 时,求b的值.
(1)、若 与 相似,求 的值;(2)、连接 , ,若 ,求 的值30. 已知直线 与抛物线 (b,c为常数, )的一个交点为 ,点 是x轴正半轴上的动点.(1)、当直线 与抛物线 (b,c为常数, )的另一个交点为该抛物线的顶点E时,求k,b,c的值及抛物线顶点E的坐标;(2)、在(1)的条件下,设该抛物线与y轴的交点为C,若点Q在抛物线上,且点Q的横坐标为b,当 时,求m的值;(3)、点D在抛物线上,且点D的横坐标为 ,当 的最小值多 时,求b的值.
-