湘教版备考2021年中考数学三轮复习专题14 最值问题
试卷更新日期:2021-06-04 类型:三轮冲刺
一、单选题
-
1. 已知实数a,b,若a>b, , 则ab的最大值是( )A、1 B、 C、2 D、22. 从 ,1,2,4四个数中任取两个不同的数(记作 )构成一个数组 (其中 ,且将 与 视为同一个数组),若满足:对于任意的 和 都有 ,则 的最大值( )A、10 B、6 C、5 D、43. 定义 ,当 时, ,当 < 时, ;已知函数 ,则该函数的最大值是( )A、-15 B、-9 C、-6 D、64. 代数式2016﹣a2+2ab﹣b2的最大值是( )A、2015 B、2016 C、2017 D、不存在5. 已知0≤x< , 那么函数y=﹣2x2+8x﹣6的最大值是( )A、-6 B、=2.5 C、2 D、不能确定6. 已知半径为1的半圆,其内接等腰梯形下底为半圆的直径,那么这个梯形周长的最大值是( )A、4 B、5 C、8 D、107. 如图,点A在半径为3的⊙O内,OA= , P为⊙O上一点,当∠OPA取最大值时,PA的长等于( )
 A、 B、 C、 D、28. 如图,长为10的线段AB的端点分别在x轴,y轴的正半轴上滑动(线段AB的长保持不变),⊙O与线段AB相切,则⊙O面积的最大值是( )
A、 B、 C、 D、28. 如图,长为10的线段AB的端点分别在x轴,y轴的正半轴上滑动(线段AB的长保持不变),⊙O与线段AB相切,则⊙O面积的最大值是( )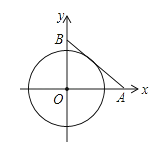 A、100π B、25π C、22π D、20π9. 如图,⊙O的半径为2,弦AB的长为2 , 以AB为直径作⊙M,点C是优弧上的一个动点,连结AC、BC分别交⊙M于点D、E,则线段CD的最大值为( )
A、100π B、25π C、22π D、20π9. 如图,⊙O的半径为2,弦AB的长为2 , 以AB为直径作⊙M,点C是优弧上的一个动点,连结AC、BC分别交⊙M于点D、E,则线段CD的最大值为( )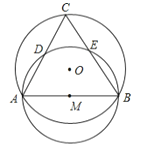 A、 B、2 C、2-2 D、4-210. 如图,⊙O是以原点为圆心, 为半径的圆,点 是直线 上的一点,过点 作⊙O的一条切线PQ , Q为切点,则切线长PQ的最小值为( )
A、 B、2 C、2-2 D、4-210. 如图,⊙O是以原点为圆心, 为半径的圆,点 是直线 上的一点,过点 作⊙O的一条切线PQ , Q为切点,则切线长PQ的最小值为( ) A、3 B、4 C、 D、11. 如图,在平面直角坐标系中,已知A(5,0)点P为线段OA上任意一点.在直线y= x上取点E,使PO=PE,延长PE到点F,使PA=PF,分别取OE、AF中点M、N,连结MN,则MN的最小值是( )
A、3 B、4 C、 D、11. 如图,在平面直角坐标系中,已知A(5,0)点P为线段OA上任意一点.在直线y= x上取点E,使PO=PE,延长PE到点F,使PA=PF,分别取OE、AF中点M、N,连结MN,则MN的最小值是( )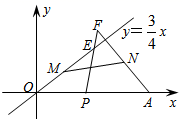 A、2.5 B、2.4 C、2.8 D、312. 如图,⊙O的半径为5,弦AB的长为6,M是AB上的动点,则线段OM长的最小值为( )
A、2.5 B、2.4 C、2.8 D、312. 如图,⊙O的半径为5,弦AB的长为6,M是AB上的动点,则线段OM长的最小值为( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
13. 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.则线段EF的最小值为 .
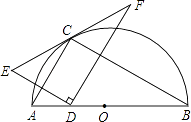 14. 二次函数 的最小值是 .15. 如图,点P是 的角平分线上一点, ,垂足为点D,且 ,点M是射线 上一动点,则 的最小值为 .
14. 二次函数 的最小值是 .15. 如图,点P是 的角平分线上一点, ,垂足为点D,且 ,点M是射线 上一动点,则 的最小值为 .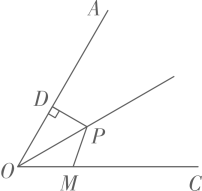 16. 在平面直角坐标系中的位置如图所示,且 ,在 内有一点 ,M , N分别是 边上的动点,连接 ,则 周长的最小值是 .
16. 在平面直角坐标系中的位置如图所示,且 ,在 内有一点 ,M , N分别是 边上的动点,连接 ,则 周长的最小值是 .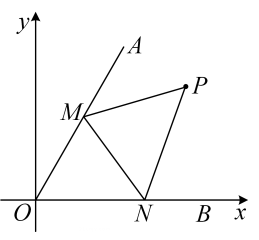 17. 直线y=x+a-3与双曲线y= 交于A,B两点,则当线段A,B的长度取最小值时,a的值为 .18. 如图,在Rt△AOB中,OA=OB=4,⊙O的半径为2,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长的最小值为 .
17. 直线y=x+a-3与双曲线y= 交于A,B两点,则当线段A,B的长度取最小值时,a的值为 .18. 如图,在Rt△AOB中,OA=OB=4,⊙O的半径为2,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长的最小值为 .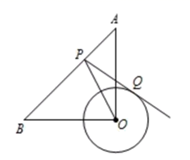 19. 如图, 中, , , , 是 内部的一个动点,且满足 ,则线段 长的最小值为.
19. 如图, 中, , , , 是 内部的一个动点,且满足 ,则线段 长的最小值为.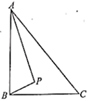 20. 如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为 .
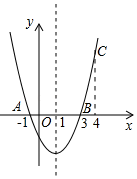
20. 如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为 .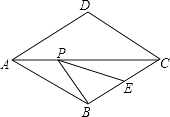 21. 如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2 , y2)是抛物线上任意一点,有下列结论:
21. 如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2 , y2)是抛物线上任意一点,有下列结论:①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1 , 则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和
其中符合题意结论的是(填序号).
 22. 如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .
22. 如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .
三、综合题
-
23. 阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:
当a>0,b>0时:
∵( )2=a﹣2 +b≥0
∴a+b≥2 ,当且仅当a=b时取等号.
请利用上述结论解决以下问题:
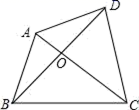 (1)、请直接写出答案:当x>0时,x+ 的最小值为 . 当x<0时,x+ 的最大值为;(2)、若y= ,(x>﹣1),求y的最小值;(3)、如图,四边形ABCD的对角线AC、BD相交于点O , △AOB、△COD的面积分别为4和9,求四边形ABCD面积的最小值.24. 已知 是关于 的函数,若其图像经过点 ,则称点 为函数图象上的“偏离点”.例如:直线 上存在“偏离点” .(1)、在双曲线 上是否存在“偏离点”?若存在,请求出“偏离点”的坐标;若不存在,请说明理由.(2)、若抛物线 上有“偏离点”,且“偏离点”为 和 ,求 的最小值(用含 的式子表示);(3)、若函数 的图像上存在唯一的一个“偏离点”,且当 时, 的最小值为 ,求 的值.25. 根据下图回答问题:
(1)、请直接写出答案:当x>0时,x+ 的最小值为 . 当x<0时,x+ 的最大值为;(2)、若y= ,(x>﹣1),求y的最小值;(3)、如图,四边形ABCD的对角线AC、BD相交于点O , △AOB、△COD的面积分别为4和9,求四边形ABCD面积的最小值.24. 已知 是关于 的函数,若其图像经过点 ,则称点 为函数图象上的“偏离点”.例如:直线 上存在“偏离点” .(1)、在双曲线 上是否存在“偏离点”?若存在,请求出“偏离点”的坐标;若不存在,请说明理由.(2)、若抛物线 上有“偏离点”,且“偏离点”为 和 ,求 的最小值(用含 的式子表示);(3)、若函数 的图像上存在唯一的一个“偏离点”,且当 时, 的最小值为 ,求 的值.25. 根据下图回答问题: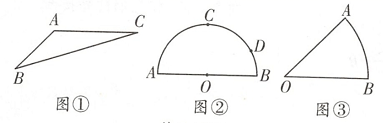 (1)、问题提出
(1)、问题提出如图①,在 中, ,求 的面积.
(2)、问题探究如图②,半圆O的直径 ,C是半圆 的中点,点D在 上,且 ,点P是 上的动点,试求 的最小值.
(3)、问题解决如图③,扇形 的半径为 在 选点P,在边 上选点E,在边 上选点F,求 的长度的最小值.
26. 在平面直角坐标系 中,关于x的二次函数 的图象过点 , . (1)、求这个二次函数的表达式;(2)、求当 时,y的最大值与最小值的差;(3)、一次函数 的图象与二次函数 的图象交点的横坐标分别是a和b,且 ,求m的取值范围.27. 有一组邻边相等的凸四边形叫做“和睦四边形”,寓意是全世界和平共处,睦邻友好,共同发展.如菱形,正方形等都是“和睦四边形”.
(1)、求这个二次函数的表达式;(2)、求当 时,y的最大值与最小值的差;(3)、一次函数 的图象与二次函数 的图象交点的横坐标分别是a和b,且 ,求m的取值范围.27. 有一组邻边相等的凸四边形叫做“和睦四边形”,寓意是全世界和平共处,睦邻友好,共同发展.如菱形,正方形等都是“和睦四边形”. (1)、如图1,BD平分∠ABC,AD∥BC,求证:四边形ABCD为“和睦四边形”;(2)、如图2,直线 与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;(3)、如图3,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:① ;②顶点D在以AB为直径的圆上. 点 是抛物线 上任意一点,且 .若 恒成立,求m的最小值.28. 如图1,抛物线y=﹣ x2+bx+c的对称轴为直线x=﹣ ,与x轴交于点A和点B(1,0),与y轴交于点C , 点D为线段AC的中点,直线BD与抛物线交于另一点E , 与y轴交于点F .
(1)、如图1,BD平分∠ABC,AD∥BC,求证:四边形ABCD为“和睦四边形”;(2)、如图2,直线 与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;(3)、如图3,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:① ;②顶点D在以AB为直径的圆上. 点 是抛物线 上任意一点,且 .若 恒成立,求m的最小值.28. 如图1,抛物线y=﹣ x2+bx+c的对称轴为直线x=﹣ ,与x轴交于点A和点B(1,0),与y轴交于点C , 点D为线段AC的中点,直线BD与抛物线交于另一点E , 与y轴交于点F . (1)、求抛物线的解析式;(2)、点P是直线BE上方抛物线上一动点,连接PD、PF , 当△PDF的面积最大时,在线段BE上找一点G , 使得PG﹣ EG的值最小,求出PG﹣ EG的最小值.(3)、如图2,点M为抛物线上一点,点N在抛物线的对称轴上,点K为平面内一点,当以A、M、N、K为顶点的四边形是正方形时,请求出点N的坐标.29. 如图1,在平面直角坐标系中,已知点A,B的坐标分别为 和 ,点E为x轴正半轴上的一个动点,过点A、B、E作 的外接圆 ,连结 并延长交圆于点D,连结 、 .
(1)、求抛物线的解析式;(2)、点P是直线BE上方抛物线上一动点,连接PD、PF , 当△PDF的面积最大时,在线段BE上找一点G , 使得PG﹣ EG的值最小,求出PG﹣ EG的最小值.(3)、如图2,点M为抛物线上一点,点N在抛物线的对称轴上,点K为平面内一点,当以A、M、N、K为顶点的四边形是正方形时,请求出点N的坐标.29. 如图1,在平面直角坐标系中,已知点A,B的坐标分别为 和 ,点E为x轴正半轴上的一个动点,过点A、B、E作 的外接圆 ,连结 并延长交圆于点D,连结 、 .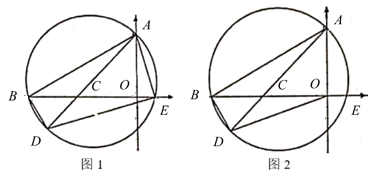 (1)、求证: .(2)、当 时,求 的长度.(3)、如图2,连结 ,求线段 的最小值及当 最小时 的外接圆圆心C的坐标.30. 在平面直角坐标系 xOy 中,等腰直角 的直角顶点C在y轴上,另两个顶点A , B在x轴上,且 ,抛物线经过A , B , C三点,如图1所示.
(1)、求证: .(2)、当 时,求 的长度.(3)、如图2,连结 ,求线段 的最小值及当 最小时 的外接圆圆心C的坐标.30. 在平面直角坐标系 xOy 中,等腰直角 的直角顶点C在y轴上,另两个顶点A , B在x轴上,且 ,抛物线经过A , B , C三点,如图1所示.
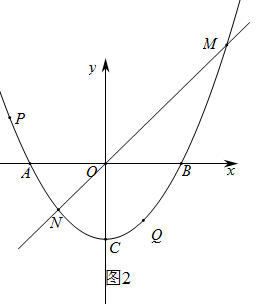 (1)、求抛物线所表示的二次函数表达式.(2)、过原点任作直线l交抛物线于M , N两点,如图2所示.
(1)、求抛物线所表示的二次函数表达式.(2)、过原点任作直线l交抛物线于M , N两点,如图2所示.①求 面积的最小值.
②已知 是抛物线上一定点,问抛物线上是否存在点P , 使得点P与点Q关于直线l对称,若存在,求出点P的坐标及直线l的一次函数表达式;若不存在,请说明理由.