湘教版备考2021年中考数学三轮复习专题16 新定义和阅读理解型

试卷更新日期：2021-06-04 类型：三轮冲刺

进入出卷网下载

一、单选题

1. （2015永州）定义[x]为不超过x的最大整数，如[3.6]=3，[0.6]=0，[﹣3.6]=﹣4．对于任意实数x ，下列式子中不正确的是（）

A、[x]=x（x为整数） B、0≤x﹣[x]＜1 C、[x+y]≤[x]+[y] D、[n+x]=n+[x]（n为整数）

查看试题解析
2. 若实数范围内定义一种运算“﹡”，使a*b=（a+1）²﹣ab，则方程（x+2）*5=0的解为（　　）

A、-2 B、﹣2，3 C、 $\frac{- 1 + \sqrt{3}}{2}$ , $\frac{- 1 - \sqrt{3}}{2}$ D、 $\frac{- 1 + \sqrt{5}}{2}$ , $\frac{- 1 - \sqrt{5}}{2}$

查看试题解析
3. 对于任意实数a、b，定义f（a，b）=a²+5a﹣b，如：f（2，3）=2²+5×2﹣3，若f（x，2）=4，则实数x的值是（　　）

A、1或﹣6 B、﹣1或6 C、﹣5或1 D、5或﹣1

查看试题解析
4. 定义新运算：对于任意实数a，b，都有a⊕b=a²﹣3a+b，如3⊕5=3²﹣3×3+5，若x⊕1=11，则实数x的值（　　）

A、2或﹣5 B、﹣2或5 C、2或5 D、﹣2或﹣5

查看试题解析
5. 定义运算：a⊗b=a（1﹣b）．下面给出了关于这种运算的几种结论：①2⊗（﹣2）=6，②a⊗b=b⊗a，③若a+b=0，则（a⊗a）+（b⊗b）=2ab，④若a⊗b=0，则a=0或b=1，其中结论正确的序号是（　　）

A、①④ B、①③ C、②③④ D、①③④

查看试题解析
6. 定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”如“967”就是一个“V数”．若十位上的数字为4，则从3，5，7，9中任选两数，能与4组成“V数”的概率是（　　）

A、 $\frac{3}{5}$ B、 $\frac{2}{5}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
7. 定义一种运算☆，其规则为a☆b= $\frac{1}{a} + \frac{1}{b}$ ，根据这个规则、计算2☆3的值是( )

A、 $\frac{5}{6}$ B、 $\frac{1}{5}$ C、5 D、6

查看试题解析

8. 先阅读下列表格：

x	…	1.1	1.2	1.3	1.4	…
x²+12x﹣15	…	﹣0.59	0.84	2.29	3.76	…

由表格可知方程x²+12x﹣15=0的正根的十分位是（　　）

A、0 B、1 C、2 D、3

查看试题解析

9. 对于任意的正数m、n定义运算※为：m※n= $\{\begin{matrix} \sqrt{m} - \sqrt{n} (m \geq n) \\ \sqrt{m} + \sqrt{n} (m < n) \end{matrix}$ ，计算（3※2）×（8※12）的结果为（　　）

A、2﹣4 $\sqrt{6}$ B、2 C、2 $\sqrt{5}$ D、20

查看试题解析
10. 对于实数a，b，我们定义符号max{a，b}的意义为：当a≥b时，max{a，b}=a；当a＜b时，max{a，b]=b，如：max{4，﹣2}=4，max{3，3}=3，若关于x的函数为y=max{x+3，﹣x+1}，则该函数的最小值是（　　）

A、0 B、2 C、3 D、4

查看试题解析
11. 对点（x，y）的一次操作变换记为p₁（x，y），定义其变换法则如下：p₁（x，y）=（x+y，x﹣y）；且规定P_n（x，y）=P₁（P_n_﹣₁（x，y））（n为大于1的整数）．例如：p₁（1，2）=（3，﹣1），p₂（1，2）=p₁（p₁（1，2））=p₁（3，﹣1）=（2，4），p₃（1，2）=p₁（p₂（1，2））=p₁（2，4）=（6，﹣2）．则p₂₀₁₄（1，﹣1）=（　　）

A、（0，2¹⁰⁰⁶） B、（2¹⁰⁰⁷ ， ﹣2¹⁰⁰⁷） C、（0，﹣2¹⁰⁰⁶） D、（2¹⁰⁰⁶ ， ﹣2¹⁰⁰⁶）

查看试题解析

二、填空题

12. 若对于实数 $x \begin{matrix} 、 \end{matrix} y$ 定义一种新运算： $x \begin{matrix} ★ \end{matrix} y = \sqrt{x y + 4}$ ，则 $(2 \begin{matrix} ★ \end{matrix} 6) \begin{matrix} ★ \end{matrix} 8$ 的值为．

查看试题解析
13. 对于任意实数a、b，定义一种运算：a※b=ab﹣a+b﹣2．例如，2※5=2×5﹣2+5﹣2=ll．请根据上述的定义解决问题：若不等式3※x＜2，则不等式的正整数解是．

查看试题解析
14. 对于实数a，b，定义运算“﹡”：a﹡b= ${\begin{matrix} a^{2} - a b (a \geq b) \\ a b - b^{2} (a < b) \end{matrix}$ ，例如4﹡2，因为4＞2，所以4﹡2=4²﹣4×2=8．若x₁ ， x₂是一元二次方程x²﹣5x+6=0的两个根，则x₁﹡x₂= ．

查看试题解析
15. 在实数范围内定义一种运算“*”，其规则为a*b=a²﹣b，根据这个规则，方程（x﹣1）*9=0的解为

查看试题解析
16. 阅读理解：对于x³﹣（n²+1）x+n这类特殊的代数式可以按下面的方法分解因式：
x³﹣（n²+1）x+n＝x³﹣n²x﹣x+n＝x（x²﹣n²）﹣（x﹣n）＝x（x﹣n）（x+n）﹣（x﹣n）＝（x﹣n）（x²+nx﹣1）．

理解运用：如果x³﹣（n²+1）x+n＝0，那么（x﹣n）（x²+nx﹣1）＝0，即有x﹣n＝0或x²+nx﹣1＝0，

因此，方程x﹣n＝0和x²+nx﹣1＝0的所有解就是方程x³﹣（n²+1）x+n＝0的解．

解决问题：求方程x³﹣5x+2＝0的解为．

查看试题解析
17. 阅读材料：设 $\vec{a}$ ＝（x₁ ， y₁）， $\vec{b}$ ＝（x₂ ， y₂），如果 $\vec{a}$ ∥ $\vec{b}$ ，则x₁•y₂＝x₂•y₁ ，根据该材料填空，已知 $\vec{a}$ ＝（4，3）， $\vec{b}$ ＝（8，m），且 $\vec{a}$ ∥ $\vec{b}$ ，则m＝.

查看试题解析
18. 阅读材料：设 $\vec{a}$ =（x₁ ， y₁）， $\vec{b}$ =（x₂ ， y₂）， $\vec{a}$ ∥ $\vec{b}$ ，则x₁•y₂=x₂•y₁ ．根据该材料填空：已知 $\vec{a}$ =（2，3）， $\vec{b}$ =（4，m），且 $\vec{a}$ ∥ $\vec{b}$ ，则m= ．

查看试题解析
19.
阅读下面材料：
如图，C是以点O为圆心，AB为直径的半圆上一点，且CO⊥AB，在OC两侧分别作矩形OGHI和正方形ODEF，且点I、F在OC上，点H、E在半圆上，求证：IG=FD．小云发现连接已知点得到两条线段，使可证明IG=FD．
请回答：小云所作的两条线段分别是和，证明IG=FD的依据是．

查看试题解析
20. 阅读下列文字与例题将一个多项式分组后，可提公因式或运用公式继续分解的方法是分组分解法．
例如：（1）　am　+an+　bm　+bn=（am+bm）+（an+bn）
=m（a+b）+n（a+b）
=（a+b）（m+n）
（2）x²﹣y²﹣2y﹣1=x²﹣（y²+2y+1）
=x²﹣（y+1）²
=（x+y+1）（x﹣y﹣1）
试用上述方法分解因式a²+2ab+ac+bc+b²= ．

查看试题解析

三、解答题

21. 对a，b定义一种新运算M，规定M（a，b）= $\frac{2 a b}{a - b}$ ，这里等式右边是通常的四则运算，例如：M（2，3）= $\frac{2 \times 2 \times 3}{2 - 3}$ =﹣12．
（1）如果M（2x，1）=M（1，﹣1），求实数x的值；
（2）若令y=M（x+ $\frac{3}{2}$ ， x﹣ $\frac{1}{2}$ ），则y是x的函数，当自变量x在﹣1≤x≤2的范围内取值时，函数值y为整数的个数记为k，求k的值．

查看试题解析
22. 定义符号min{a，b}的含义为：当a≥b时，min{a，b}=b；当a＜b时，min{a，b}=a．如：min{1，﹣2}=﹣2，min{﹣1，2}=﹣1．
（1）求min{x²﹣1，﹣2}；
（2）已知min{x²﹣2x+k，﹣3}=﹣3，求实数k的取值范围；
（3）已知当﹣2≤x≤3时，min{x²﹣2x﹣15，m（x+1）}=x²﹣2x﹣15．直接写出实数m的取值范围．

查看试题解析
23. 在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S=ah．例如：三点坐标分别为A（1，2），B（﹣3，1），C（2，﹣2），则“水平底”a=5，“铅垂高”h=4，“矩面积”S=ah=20．已知点A（1，2），B（﹣3，1），P（0，t）．
（1）若A，B，P三点的“矩面积”为12，求点P的坐标；
（2）直接写出A，B，P三点的“矩面积”的最小值．

查看试题解析
24.
联想三角形内心的概念，我们可引入如下概念．
定义：到三角形的两边距离相等的点，叫做此三角形的准内心．
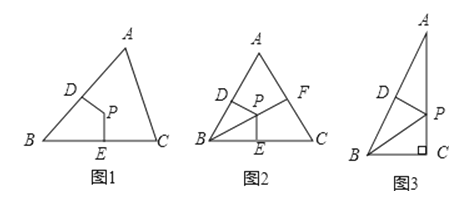
举例：如图1，若PD=PE，则点P为△ABC的准内心．
应用：如图2，BF为等边三角形的角平分线，准内心P在BF上，且PF= $\frac{1}{2}$ BP，求证：点P是△ABC的内心．
探究：已知△ABC为直角三角形，∠C=90°，准内心P在AC上，若PC= $\frac{1}{2}$ AP，求∠A的度数．

查看试题解析
25.
阅读材料：如图，△ABC中，AB=AC，P为底边BC上任意一点，点P到两腰的距离分别为r₁ ， r₂ ，腰上的高为h，连接AP，则S_△_ABP+S_△_ACP=S_△_ABC ，即： $\frac{1}{2}$ AB•r₁+ $\frac{1}{2}$ AC•r₂= $\frac{1}{2}$ AB•h，∴r₁+r₂=h

(1)、理解与应用
如果把“等腰三角形”改成“等边三角形”，那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”，即：已知边长为2的等边△ABC内任意一点P到各边的距离分别为r₁ ， r₂ ， r₃ ，试证明：r₁+r₂+r₃= $\sqrt{3}$ ．

(2)、类比与推理
边长为2的正方形内任意一点到各边的距离的和等于

(3)、拓展与延伸
若边长为2的正n边形A₁A₂…An内部任意一点P到各边的距离为r₁ ， r₂ ， …r_n ，请问r₁+r₂+…r_n是否为定值（用含n的式子表示），如果是，请合理猜测出这个定值．

查看试题解析
26. 阅读材料，回答问题：材料：为解方程x⁴﹣x²﹣6=0，然后设x²=y，于是原方程可化为y²﹣y﹣6=0，解得y₁=﹣2，y₂=3．当y=﹣2时，x²=﹣2不合题意舍去；当y=3时，x²=3，解得x₁= $\sqrt{3}$ ， x₂=﹣ $\sqrt{3}$ ．故原方程的根为x₁= $\sqrt{3}$ ， x₂=﹣ $\sqrt{3}$ ．
请你参照材料给出的解题方法，解下列方程
①（x²﹣x）²﹣4（x²﹣x）﹣12=0．
② $\frac{2 x - 1}{x}$ ﹣ $\frac{3 x}{2 x - 1}$ =2．

查看试题解析
27. 阅读下列材料，然后回答问题：
在进行二次根式运算时，我们有时会碰上如 $\frac{5}{\sqrt{3}}$ 、 $\frac{2}{\sqrt{3} + 1}$ 这样的式子，其实我们还可以将其进一步化简： $\frac{5}{\sqrt{3}}$ = $\frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}$ = $\frac{5}{3} \sqrt{3}$ ；
$\frac{2}{\sqrt{3} + 1}$ = $\frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)}$ = $\frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1}$ = $\sqrt{3}$ -1．以上这种化简过程叫做分母有理化．
$\frac{2}{\sqrt{3} + 1}$ 还可以用以下方法化简： $\frac{2}{\sqrt{3} + 1}$ = $\frac{3 - 1}{\sqrt{3} + 1}$ = $\frac{{(\sqrt{3})}^{2} - 1^{2}}{\sqrt{3} + 1}$ = $\frac{(\sqrt{3} + 1) (\sqrt{3} - 1)}{\sqrt{3} + 1}$ = $\sqrt{3}$ -1．
（1）请用其中一种方法化简 $\frac{4}{\sqrt{15} - \sqrt{11}}$ ；
（2）化简： $\frac{2}{\sqrt{3} + 1}$ + $\frac{2}{\sqrt{5} + \sqrt{3}}$ + $\frac{2}{\sqrt{7} + \sqrt{5}}$ +...+ $\frac{2}{\sqrt{99} + \sqrt{97}}$ ．

查看试题解析
28. 阅读探索：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”（完成下列空格）
（1）当已知矩形A的边长分别为6和1时，小亮同学是这样研究的：
设所求矩形的两边分别是x和y，由题意得方程组： $\{\begin{matrix} x + y = \frac{7}{2} \\ x y = 3 \end{matrix}$ ，消去y化简得：2x²﹣7x+6=0，
∵△=49﹣48＞0，∴x₁=?x₂=　?　，
∴满足要求的矩形B存在．
（2）如果已知矩形A的边长分别为2和1，请你仿照小亮的方法研究是否存在满足要求的矩形B．
（3）如果矩形A的边长为m和n，请你研究满足什么条件时，矩形B存在？

查看试题解析
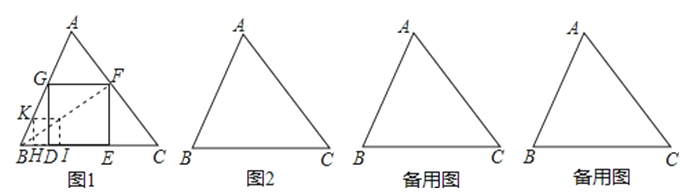
29.
如图1，给定锐角三角形ABC，小明希望画正方形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上，他发现直接画图比较困难，于是他先画了一个正方形HIJK，是的H，I，位于射线BC上，K位于射线BA上，而不需要求J必须位于AC上．这是他发现可以将正方形HIJK通过放大或缩小得到满足要求的正方形DEFG．
阅读以上材料，回答小明接下来研究的以下问题：
（1）如图2，给定锐角三角形ABC，画出所有长宽比为2：1的长方形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上．
（2）已知三角形ABC的面积为36，BC=12，在第（1）问的条件下，求长方形DEFG的面积．

查看试题解析
30. 【阅读材料】已知，如图1，在面积为S的△ABC中，BC=a，AC=b，AB=c，内切圆O的半径为r，连接OA，OB，OC，△ABC被划分为三个小三角形．
∵S=S_△_OBC+S_△_OAC+S_△_OAB= $\frac{1}{2}$ BC•r+ $\frac{1}{2}$ AC•r+ $\frac{1}{2}$ AB•r= $\frac{1}{2}$ ar+ $\frac{1}{2}$ br+ $\frac{1}{2}$ cr= $\frac{1}{2}$ （a+b+c）r．
∴r= $\frac{2 S}{a + b + c}$ ．
（1）【类比推理】如图2，若面积为S的四边形ABCD存在内切圆（与各边都相切的圆），各边长分别为AB=a，BC=b，CD=c，AD=d，求四边形的内切圆半径r的值；
（2）【理解应用】如图3，在Rt△ABC中，内切圆O的半径为r，⊙O与△ABC各边分别相切于D、E和F，已知AD=3，BD=2，求r的值．

查看试题解析
31. 阅读下列解答过程，并回答问题．
在（x²+ax+b）（2x²﹣3x﹣1）的积中，x³项的系数为﹣5，x²项的系数为﹣6，求a，b的值．
解：（x²+ax+b）•（2x²﹣3x﹣1）=
2x⁴﹣3x³+2ax³+3ax²﹣3bx=①
2x⁴﹣（3﹣2a）x³﹣（3a﹣2b）x²﹣3bx ②
根据对应项系数相等，有 $\{\begin{matrix} 3 - 2 a = - 5 \\ 3 a - 2 b = - 6 \end{matrix}$ 解得 $\{\begin{matrix} a = 4 \\ b = 9 \end{matrix}$
回答：
（1）上述解答过程是否正确？　　．
（2）若不正确，从第　　步开始出现错误，其他步骤是否还有错误？　　．
（3）写出正确的解答过程．

查看试题解析
32. 观察与思考：阅读下列材料，并解决后面的问题．
在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c，过A作 AD⊥BC于D(如图)，则sinB= $\frac{A D}{c}$ ， sinC= $\frac{A D}{b}$ ，即AD=csinB，AD=bsinC，于是csinB=bsinC，即 $\frac{b}{\sin B}$ = $\frac{c}{\sin C}$ .同理有： $\frac{c}{\sin C}$ = $\frac{a}{\sin A}$ ， $\frac{a}{\sin A}$ = $\frac{b}{\sin B}$ ，所以 $\frac{a}{\sin A}$ = $\frac{b}{\sin B}$ = $\frac{c}{\sin C}$
即：在一个三角形中，各边和它所对角的正弦的比相等．在锐角三角形中，若已知三个元素（至少有一条边），运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料，完成下列各题.
（1）如图，△ABC中，∠B=45⁰ ， ∠C=75⁰ ， BC=60，则∠A= ；AC= ；
（2）如图，一货轮在C处测得灯塔A在货轮的北偏西30°的方向上，随后货轮以60海里／时的速度按北偏东30°的方向航行，半小时后到达B处，此时又测得灯塔A在货轮的北偏西75°的方向上(如图)，求此时货轮距灯塔A的距离AB.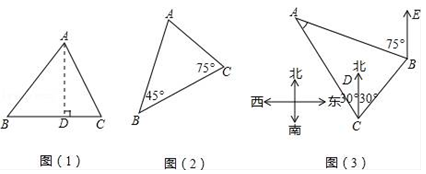

查看试题解析
33.
定义：如图，若双曲线 $y = \frac{k}{x}$ （k＞0）与它的其中一条对称轴y=x相交于两点A，B，则线段AB的长称为双曲线 $y = \frac{k}{x}$ （k＞0）的对径．

（1）求双曲线 $y = \frac{1}{x}$ 的对径；
（2）若某双曲线 $y = \frac{k}{x}$ （k＞0）的对径是 $10 \sqrt{2}$ ．求k的值．

查看试题解析
34. 平面直角坐标系xOy中，点A（x₁ ， y₁）与B（x₂ ， y₂），如果满足x₁+x₂=0，y₁﹣y₂=0，其中x₁≠x₂ ，则称点A与点B互为反等点．已知：点C（3，4）

(1)、下列各点中，点C互为反等点；
D（﹣3，﹣4），E（3，4），F（﹣3，4）

(2)、已知点G（﹣5，4），连接线段CG，若在线段CG上存在两点P，Q互为反等点，求点P的横坐标x_P的取值范围；

(3)、已知⊙O的半径为r，若⊙O与（2）中线段CG的两个交点互为反等点，求r的取值范围．

查看试题解析