湘教版备考2021年中考数学三轮复习专题17 探究型问题
试卷更新日期:2021-06-04 类型:三轮冲刺
一、单选题
-
1. 我们在探究二次函数的图象与性质时,首先从y=ax2(a≠0)的形式开始研究,最后到y=a(x-h)2+k(a≠0)的形式,这种探究问题的思路体现的数学思想是( )A、转化 B、由特殊到一般 C、分类讨论 D、数形结合2.
九年级的小玲从小就喜欢画画,探究问题.下面请看她的探究过程:
(a)以AB为直径画半⊙O;(b)在半⊙O上任意取一点C;(c)画∠ACB的平分线与AB相交于点D; (d)画CD的中垂线m与AC、BC分别相交于E、F;(d)连接DE、DF.
结果她发现:(1)∠ADE与∠BDF互余;(2)四边形CEDF为正方形;(3)△AED与△DFB相似;(4)把△BFD绕着D点按逆时针方向旋转90°,B点的位置恰好在△ABC的AC边的直线上.
则你认为其中正确的有( )
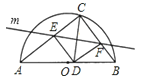 A、1个 B、2个 C、3个 D、4个3.
A、1个 B、2个 C、3个 D、4个3.如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为6m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
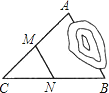 A、AB=12m B、MN∥AB C、△CMN∽△CAB D、CM:MA=1:24.
A、AB=12m B、MN∥AB C、△CMN∽△CAB D、CM:MA=1:24.在研究相似问题时,甲、乙同学的观点如下:
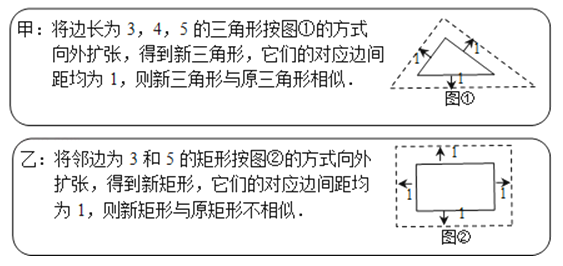
对于两人的观点,下列说法正确的是( )
A、两人都对 B、两人都不对 C、甲对,乙不对 D、甲不对,乙对5.在小孔成像问题中,如图可知CD的长是物长AB长的( )
 A、3倍 B、 C、 D、6. 如图,点A,B的坐标分别为 、 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,当 最大时,M点的坐标为( )
A、3倍 B、 C、 D、6. 如图,点A,B的坐标分别为 、 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,当 最大时,M点的坐标为( )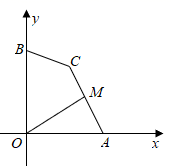 A、 B、 C、 D、7. 如图1,在平面直角坐标系中, 在第一象限,且 轴.直线 从原点 出发沿x轴正方向平移.在平移过程中,直线被 截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示.那么 的面积为( )
A、 B、 C、 D、7. 如图1,在平面直角坐标系中, 在第一象限,且 轴.直线 从原点 出发沿x轴正方向平移.在平移过程中,直线被 截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示.那么 的面积为( )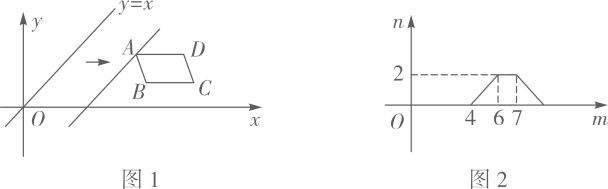 A、3 B、 C、6 D、8. 课堂上,老师给出一道题:如图,将抛物线C:y=x2﹣6x+5在x轴下方的图象沿x轴翻折,翻折后得到的图象与抛物线C在x轴上方的图象记为G,已知直线l:y=x+m与图象G有两个公共点,求m的取值范围甲同学的结果是﹣5<m<﹣1,乙同学的结果是m> .下列说法正确的是( )
A、3 B、 C、6 D、8. 课堂上,老师给出一道题:如图,将抛物线C:y=x2﹣6x+5在x轴下方的图象沿x轴翻折,翻折后得到的图象与抛物线C在x轴上方的图象记为G,已知直线l:y=x+m与图象G有两个公共点,求m的取值范围甲同学的结果是﹣5<m<﹣1,乙同学的结果是m> .下列说法正确的是( )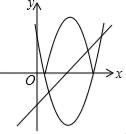 A、甲的结果符合题意 B、乙的结果符合题意 C、甲、乙的结果合在一起才正确 D、甲、乙的结果合在一起也不正确9. 如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( )
A、甲的结果符合题意 B、乙的结果符合题意 C、甲、乙的结果合在一起才正确 D、甲、乙的结果合在一起也不正确9. 如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( )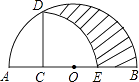 A、 B、 C、 D、10.
A、 B、 C、 D、10.为了备战世界杯,中国足球队在某次集训中,一队员在距离球门12米处的挑射,正好射中了2.4米高的球门横梁.若足球运行的路线是抛物线y=ax2+bx+c(如图),则下列结论:①a<-;②-<a<0; ③a-b+c>0;④0<b<-12a.其中正确的是( )
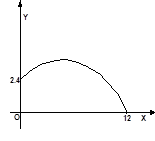 A、①③ B、①④ C、②③ D、②④11.
A、①③ B、①④ C、②③ D、②④11.如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是( )
 A、
A、 B、
B、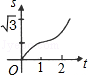 C、
C、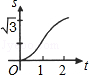 D、
D、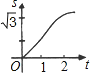 12. 用图象法探索二次函数y=x2和反比例函数y=(k不为零)交点个数为( )
12. 用图象法探索二次函数y=x2和反比例函数y=(k不为零)交点个数为( )
A、一定是1个 B、一定有2个 C、1个或者2个 D、0个13.小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=﹣3.4,则方程的另一个近似根(精确到0.1)为( )
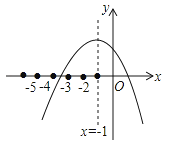 A、4.4 B、3.4 C、2.4 D、1.414.
A、4.4 B、3.4 C、2.4 D、1.414.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0).根据这个规律探索可得,第100个点的坐标为( )
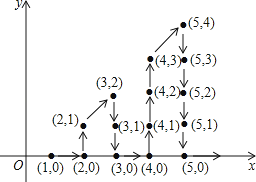 A、(14,8) B、(13,0) C、(100,99) D、(15,14)15. 下表示用计算器探索函数y=x2+5x﹣3时所得的数值:
A、(14,8) B、(13,0) C、(100,99) D、(15,14)15. 下表示用计算器探索函数y=x2+5x﹣3时所得的数值:x
0
0.25
0.5
0.75
1
y
﹣3
﹣1.69
﹣0.25
1.31
3
则方程x2+5x﹣3=0的一个解x的取值范围为( )
A、0<x<0.25 B、0.25<x<0.5 C、0.5<x<0.75 D、0.75<x<116. 表是用计算器探索函数y=2x2﹣2x﹣10所得的数值,则方程2x2﹣2x﹣10=0的一个近似解为( )x
﹣2.1
﹣2.2
﹣2.3
﹣2.4
y
﹣1.39
﹣0.76
﹣0.11
0.56
A、x=﹣2.1 B、x=﹣2.2 C、x=﹣2.3 D、x=﹣2.417.如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底(B)7.8米的点E处,然后观察者沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB)的高度约为( )米.
 A、15.6 B、6.4 C、3.4 D、3.918. 小明在学习了利用图象法来求一元二次方程的近似根的知识后进行了尝试:在直角坐标系中作出二次函数y=x2+2x﹣10的图象,由图象可知,方程x2+2x﹣10=0有两个根,一个在﹣5和﹣4之间,另一个在2和3之间.利用计算器进行探索:由下表知,方程的一个近似根是( )
A、15.6 B、6.4 C、3.4 D、3.918. 小明在学习了利用图象法来求一元二次方程的近似根的知识后进行了尝试:在直角坐标系中作出二次函数y=x2+2x﹣10的图象,由图象可知,方程x2+2x﹣10=0有两个根,一个在﹣5和﹣4之间,另一个在2和3之间.利用计算器进行探索:由下表知,方程的一个近似根是( )x
﹣4.1
﹣4.2
﹣4.3
﹣4.4
y
﹣1.39
﹣0.76
﹣0.11
0.56
A、﹣4.1 B、﹣4.2 C、﹣4.3 D、﹣4.4二、填空题
-
19. 某学习小组为了探究函数y=x2﹣|x|的图象和性质,根据以往学习函数的经验,列表确定了该函数图象上一些点的坐标,表格中的m= .
x
…
﹣2
﹣1.5
﹣1
﹣0.5
0
0.5
1
1.5
2
…
y
…
2
0.75
0
﹣0.25
0
﹣0.25
0
m
2
…
20. 小亮同学在探究一元二次方程ax2+bx+c=0的近似解时,填好了下面的表格:x
3.23
3.24
3.25
3.26
ax2+bx+c
﹣0.06
﹣0.02
0.03
0.09
根据以上信息请你确定方程ax2+bx+c=0的一个解的范围是 .
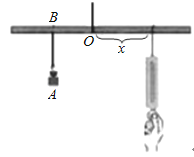
21.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
x(cm)…10
15
20
25 30…
y(N)…30
20
15
12 10…
猜测y与x之间的函数关系,并求出函数关系式为 .
 22. 探索与发现:下面是用分数(数字表示面积)砌成的“分数墙”,则整面“分数墙”的总面积是 .
22. 探索与发现:下面是用分数(数字表示面积)砌成的“分数墙”,则整面“分数墙”的总面积是 .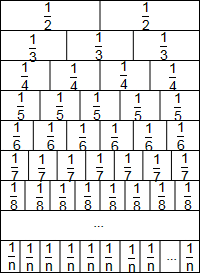 23. 算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大的贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字如图:
23. 算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大的贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字如图:数字
形式
1
2
3
4
5
6
7
8
9
纵式
|
||
|||
||||
|||||




横式






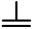


表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空.示例如下:
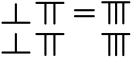 ,则
,则  |
| 
 表示的数是 . 24. 找出如下图形变化的规律,则第100个图形中黑色正方形的数量是 .
表示的数是 . 24. 找出如下图形变化的规律,则第100个图形中黑色正方形的数量是 .
三、解答题
-
25.
依据闯关游戏规则,请你探究“闯关游戏”的奥秘:


(1)用列表的方法表示所有可能的闯关情况;
(2)求出闯关成功的概率。26.如图,在平面直角坐标系中,函数y=x的图象l是第一、三象限的角平分线.
实验与探究:
由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出它们的坐标:B′ 、C′ ;
归纳与发现:
结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线L的对称点P′的坐标为 .
 27.
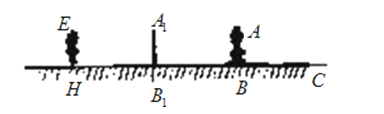
27.学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH.
 28.
28.(1)探究新知:

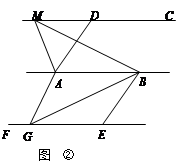
①如图,已知AD∥BC , AD=BC , 点M , N是直线CD上任意两点.试判断△ABM与△ABN的面积是否相等。
②如图,已知AD∥BE , AD=BE , AB∥CD∥EF , 点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由.
(2)结论应用:
如图③,抛物线的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D . 试探究在抛物线上是否存在除点C以外的点E , 使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
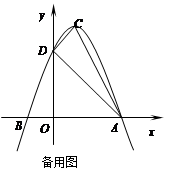 29.
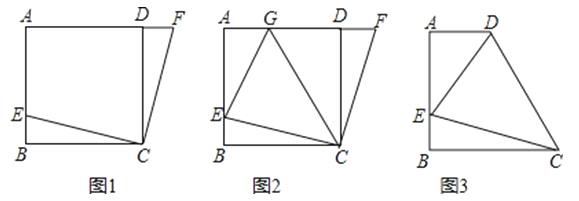
29.感知:如图1,在正方形ABCD中,E是AB上一点,将点E绕点C顺时针旋转90°到点F,易知△CEB≌△CFD.
探究:如图2,在图1中的基础上作∠ECF的角平分线CG,交AD于点G,连接EG,求证:EG=BE+GD.
应用:如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC.E是AB上一点,且∠DCE=45°,AD=6,DE=10,求直角梯形ABCD的面积.
 30.
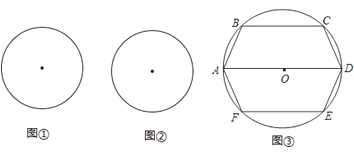
30.如图,圆O的半径为r.
(1)在图①中,画出圆O的内接正△ABC,简要写出画法;求出这个正三角形的周长.
(2)在图②中,画出圆O的内接矩形ABCD,简要写出画法;若设AB=x,求出矩形的周长.
(3)如图③,六边形ABCDEF内接于半径为r(常数)的⊙O,其中AD为直径,且AB=CD=DE=FA.设AB=x,求六边形ABCDEF的周长L关于x的函数关系式,并探究L是否有最大值,若有,请指出x为何值时,L取得最大值;若没有,请说明理由.
 31.
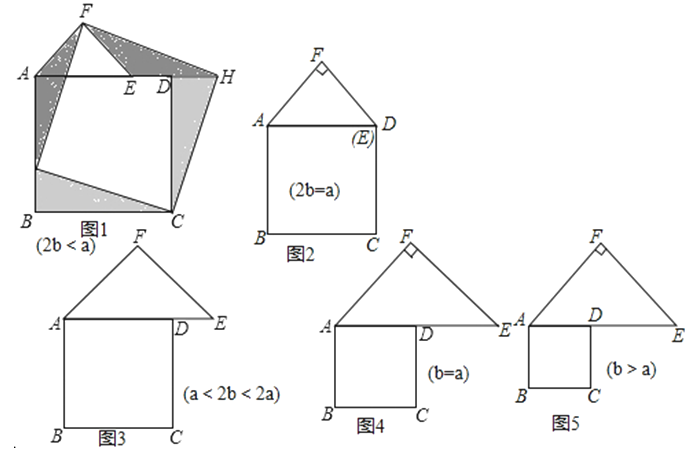
31.在图1至图5中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.
操作示例:
当2b<a时,如图(1),在BA上选取点G,使BG=b,连接FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH.
思考发现:
小明在操作后发现:该剪拼方法就是先将△FAG绕点F逆时针旋转90度到△FEH的位置,易知EH与AD在同一直线上.连接CH,由剪拼方法可得DH=BG,故△CHD≌△CGB,从而又可将△CGB绕点G顺时针旋转90度到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图),过点F作FM⊥AE于点M(图略),利用SAS公理可判断△HFM≌△CHD,易得FH=HC=GC=FG,.∠FHC=90°进而根据正方形的判定方法,可以判断出四边形FGCH是正方形.
实践探究:
正方形的面积是多少;(用含a,b,的式子表示)
类比图1的剪拼方法,请你就图2﹣图4的三种情形分别画出剪拼成一个新正方形的示意图.
联想拓展:
小明通过探究后发现:当b≤a,此类图形都能剪拼成正方形,且所选取的点G的位置在BA方向上随着b的增大不断上移;当b>a时,如图的图形能否剪拼成一个正方形?若能,请你在图中画出剪拼的示意图;若不能,简要说明理由.
32. 设a1=32﹣12 , a2=52﹣32 , …,an=(2n+1)2﹣(2n﹣1)2(n为大于0的自然数).
(1)探究an是否为8的倍数,并用文字语言表述你所获得的结论;
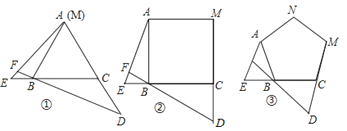
(2)若一个数的算术平方根是一个自然数,则称这个数是“完全平方数”.试找出a1 , a2 , …,an , …这一列数中从小到大排列的前4个完全平方数,并指出当n满足什么条件时,an为完全平方数(不必说明理由).33.如图③,点E,D分别是正三角形ABC,正四边形ABCM,正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点,且△ABE与△BCD能相互重合,DB的延长线交AE于点F.
(1)在图①中,求∠AFB的度数;
(2)在图②中,∠AFB的度数为,图③中,∠AFB的度数为;
(3)继续探索,可将本题推广到一般的正n边形情况,用含n的式子表示∠AFB的度数.
 34. 关于x的函数y=2mx2+(1﹣m)x﹣1﹣m(m是实数),探索发现了以下四条结论:
34. 关于x的函数y=2mx2+(1﹣m)x﹣1﹣m(m是实数),探索发现了以下四条结论:①函数图象与坐标轴总有三个不同的交点;
②当m=﹣3时,函数图象的顶点坐标是( , );
③当m>0时,函数图象截x轴所得的线段长度大于;
④当m≠0时,函数图象总经过两个定点.
请你判断四条结论的真假,并说明理由.
四、综合题
-
35. 为了探索函数 的图象与性质,我们参照学习函数的过程与方法.
列表:
描点:在平面直角坐标系中,以自变量 的取值为横坐标,以相应的函数值 为纵坐标,描出相应的点,如图 所示:
 (1)、如图 ,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,作出函数图象;(2)、已知点 在函数图象上,结合表格和函数图象,回答下列问题:
(1)、如图 ,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,作出函数图象;(2)、已知点 在函数图象上,结合表格和函数图象,回答下列问题:若 ,则 ;
若 ,则 ;
若 ,则 (填“>”,“=”,“<”).
(3)、某农户要建造一个图 所示的长方体形无盖水池,其底面积为 平方米,深为 米.已知底面造价为 千元/平方米,侧面造价为 千元/平方米,设水池底面一边的长为 米,水池总造价为 千元.①请写出 与 的函数关系式;
②若该农户预算不超过 千元,则水池底面一边的长 应控制在什么范围内?