湘教版备考2021年中考数学三轮复习专题18 综合问题
试卷更新日期:2021-06-04 类型:三轮冲刺
一、单选题
-
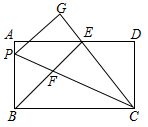
1. 如图,在矩形 中, , , 平分 ,与对角线 相交于点 , 是线段 的中点,则下列结论中:① ;② ;③ ;④ ,正确的有( )个
 A、1 B、2 C、3 D、42. 如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是( )
A、1 B、2 C、3 D、42. 如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是( )
⑴EF= OE;
⑵S四边形OEBF:S正方形ABCD=1:4;
⑶BE+BF= OA;
⑷在旋转过程中,当△BEF与△COF的面积之和最大时,AE= ;
⑸OG•BD=AE2+CF2 .
A、(1)(2)(3)(5) B、(1)(3)(4)(5) C、(2)(3)(4)(5) D、(1)(2)(3)(4)3. 已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连接CM.分析下列结论:①AP⊥BN;②BM=DN;③点P一定在以CM为直径的圆上;④当AN= 时,PC= .其中结论正确的个数是( ) A、1个 B、2个 C、3个 D、4个4. 如图,已知二次函数 的图象交 轴于 两点,交 轴于点 ,对称轴为直线 .直线 与二次函数的图象交于 两点, 点在 轴的下方,而且 的横坐标小于4,下列结论:
A、1个 B、2个 C、3个 D、4个4. 如图,已知二次函数 的图象交 轴于 两点,交 轴于点 ,对称轴为直线 .直线 与二次函数的图象交于 两点, 点在 轴的下方,而且 的横坐标小于4,下列结论:① ;② ;③ ;④不等式 的取值范围是 .其中正确的结论有( )
 A、1个 B、2个 C、3个 D、4个5. 如图是抛物线 的部分图象,其对称轴为直线 且与x轴的一个交点坐标是 ,则下列结论:① ;② ;③ ;④ (m为任意实数).其中正确结论的个数是( )
A、1个 B、2个 C、3个 D、4个5. 如图是抛物线 的部分图象,其对称轴为直线 且与x轴的一个交点坐标是 ,则下列结论:① ;② ;③ ;④ (m为任意实数).其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个6. 如图,在矩形ABCD中,AD=10,在BC边上取一点E , 连接AE、DE , 使得DE=AD , H为AE中点,连接DH , 在DE上取一点F , 连接AF , 将△AEF沿着AF翻折得到△AGF , 且GF⊥AD于M , 连接GD , 若AE=4 ,则点F到直线DG的距离为( )
A、1个 B、2个 C、3个 D、4个6. 如图,在矩形ABCD中,AD=10,在BC边上取一点E , 连接AE、DE , 使得DE=AD , H为AE中点,连接DH , 在DE上取一点F , 连接AF , 将△AEF沿着AF翻折得到△AGF , 且GF⊥AD于M , 连接GD , 若AE=4 ,则点F到直线DG的距离为( ) A、2 B、 C、 D、7. 如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1的长为半径画弧,交直线y= x于点B1;过点B1作B1A2∥y轴交直线y=2x于点A2 , 以O为圆心,OA2长为半径画弧,交直线y= x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3 , 以点O为圆心,OA3长为半径画弧,交直线y= x于点B3;…按如此规律进行下去,点B2021的坐标为( )
A、2 B、 C、 D、7. 如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1的长为半径画弧,交直线y= x于点B1;过点B1作B1A2∥y轴交直线y=2x于点A2 , 以O为圆心,OA2长为半径画弧,交直线y= x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3 , 以点O为圆心,OA3长为半径画弧,交直线y= x于点B3;…按如此规律进行下去,点B2021的坐标为( ) A、(22021 , 22021) B、(22021 , 22020) C、(22020 , 22021) D、(22022 , 22021)8. 如图,点A、M是第一象限内双曲线 (k为常数, , )上的点(点M在点A的左侧),若M点的纵坐标为1,且△OAM为等边三角形,则k的值为( )
A、(22021 , 22021) B、(22021 , 22020) C、(22020 , 22021) D、(22022 , 22021)8. 如图,点A、M是第一象限内双曲线 (k为常数, , )上的点(点M在点A的左侧),若M点的纵坐标为1,且△OAM为等边三角形,则k的值为( ) A、 B、 C、 D、9. 如图, , , ,…是分别以A1 , A2 , A3 , …为直角顶点,一条直角边在x轴正半轴上的等腰直角三角形,其斜边的中点C1(x1 , y1),C2(x2 , y2),C3(x3 , y3),…均在反比例函数 的图象上,则 的值为( )
A、 B、 C、 D、9. 如图, , , ,…是分别以A1 , A2 , A3 , …为直角顶点,一条直角边在x轴正半轴上的等腰直角三角形,其斜边的中点C1(x1 , y1),C2(x2 , y2),C3(x3 , y3),…均在反比例函数 的图象上,则 的值为( )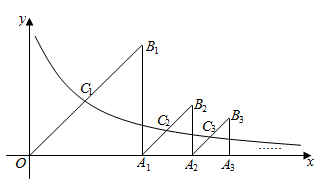 A、 B、 C、 D、10. 如图,是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A , B两点,下列结论:①2a+b=0;m+n=3;②抛物线与x轴的另一个交点是(﹣1,0);③方程ax2+bx+c=3有两个相等的实数根;④当1 x 4时,有y2 y1;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=1.正确的为( )
A、 B、 C、 D、10. 如图,是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A , B两点,下列结论:①2a+b=0;m+n=3;②抛物线与x轴的另一个交点是(﹣1,0);③方程ax2+bx+c=3有两个相等的实数根;④当1 x 4时,有y2 y1;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=1.正确的为( )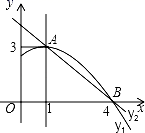 A、①④⑤ B、①③④ C、①③⑤ D、①②③11. 如图,矩形 的四个顶点分别在矩形 的各条边上, , , .有以下四个结论:① ;② ;③ ;④矩形 的面积是 .其中正确的结论为( )
A、①④⑤ B、①③④ C、①③⑤ D、①②③11. 如图,矩形 的四个顶点分别在矩形 的各条边上, , , .有以下四个结论:① ;② ;③ ;④矩形 的面积是 .其中正确的结论为( ) A、①② B、①②③ C、①②④ D、①②③④12. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=1,下列结论:①2a+b=0;②9a+c>3b;③若点A(﹣3,y1)、点B(﹣ ,y2)、点C( ,y3)在该函数图象上,则y1<y3<y2:④若方程ax2+bx+c=﹣3(a≠0)的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<3<x2;⑤m(am+b)﹣b<a . 其中正确的结论有( )
A、①② B、①②③ C、①②④ D、①②③④12. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=1,下列结论:①2a+b=0;②9a+c>3b;③若点A(﹣3,y1)、点B(﹣ ,y2)、点C( ,y3)在该函数图象上,则y1<y3<y2:④若方程ax2+bx+c=﹣3(a≠0)的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<3<x2;⑤m(am+b)﹣b<a . 其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个13. 如图,平行于x轴的直线与函数y= (k1>0,x>0),y= (k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为6,则k1﹣k2的值为( )
A、1个 B、2个 C、3个 D、4个13. 如图,平行于x轴的直线与函数y= (k1>0,x>0),y= (k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为6,则k1﹣k2的值为( ) A、12 B、﹣12 C、6 D、﹣614. 如图,在矩形ABCD中,AB=12,P是AB上一点,将△PBC沿直线PC折叠,顶点B的对应点是G , 过点B作BE⊥CG , 垂足为E , 且在AD上,BE交PC于点F , 则下列结论,其中正确的结论有( )
A、12 B、﹣12 C、6 D、﹣614. 如图,在矩形ABCD中,AB=12,P是AB上一点,将△PBC沿直线PC折叠,顶点B的对应点是G , 过点B作BE⊥CG , 垂足为E , 且在AD上,BE交PC于点F , 则下列结论,其中正确的结论有( )①BP=BF;②若点E是AD的中点,那么△AEB≌△DEC;③当AD=25,且AE<DE时,则DE=16;④在③的条件下,可得sin∠PCB= ;⑤当BP=9时,BE•EF=108.
 A、2个 B、3个 C、4个 D、5个15. 如图,在正方形ABCD中,点E是CD的中点,点F是BC上的一点,且BF=3CF,连接AE、AF、EF,下列结论:①∠DAE=30°,②△ADE∽△ECF,③AE⊥EF,④AE2=AD•AF,其中正确结论的个数是( )
A、2个 B、3个 C、4个 D、5个15. 如图,在正方形ABCD中,点E是CD的中点,点F是BC上的一点,且BF=3CF,连接AE、AF、EF,下列结论:①∠DAE=30°,②△ADE∽△ECF,③AE⊥EF,④AE2=AD•AF,其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
16. 如图,某数学兴趣小组在学完矩形的知识后一起探讨了一个纸片折叠问题:如何将一张平行四边形纸片 的四个角向内折起,拼成一个无缝隙、无重叠的矩形 .图中 , , , 表示折痕,折后 的对应点分别是 .若 , , ,则纸片折叠时 的长应取 .
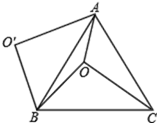
 17. 如图,O是正△ABC内一点, , , ,将线段BO以点B为旋转中心逆时针旋转60°得到线段 ,下列结论正确的有 . (请填序号)
17. 如图,O是正△ABC内一点, , , ,将线段BO以点B为旋转中心逆时针旋转60°得到线段 ,下列结论正确的有 . (请填序号)①点O与 的距离为4;② ;③ ;④ .
 18. 已知三角形三边分别为3、4、5,则该三角形内心与外心之间的距离为 .19. 反比例函数y= 的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+ =0的根的情况是 .
18. 已知三角形三边分别为3、4、5,则该三角形内心与外心之间的距离为 .19. 反比例函数y= 的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+ =0的根的情况是 . 20. 如图,直线y=4﹣x与双曲线y 交于A , B两点,过B作直线BC⊥y轴,垂足为C , 则以OA为直径的圆与直线BC的交点坐标是 .
20. 如图,直线y=4﹣x与双曲线y 交于A , B两点,过B作直线BC⊥y轴,垂足为C , 则以OA为直径的圆与直线BC的交点坐标是 .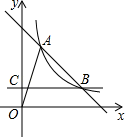 21. 已知: ……则 的末尾数字是.22. 如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=8cm,EF=15cm,则边AD的长是cm.
21. 已知: ……则 的末尾数字是.22. 如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=8cm,EF=15cm,则边AD的长是cm. 23. 直线y=k1x+b1(k1>0)与y=k2x+b2(k2<0)相交于点(-3,0),且两直线与y轴围成的三角形面积为15,那么b1-b2等于 .24. 已知如图,四边形ABCD为矩形,点O是AC的中点,过点O的一直线分别与AB、CD交于点E、F , 连接BF交AC于点M , 连接DE、BO , 若∠COB=60°,FO=FC , 则下列结论:①FB⊥OC , OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB:OE=3:2,其中符合题意结论是 .
23. 直线y=k1x+b1(k1>0)与y=k2x+b2(k2<0)相交于点(-3,0),且两直线与y轴围成的三角形面积为15,那么b1-b2等于 .24. 已知如图,四边形ABCD为矩形,点O是AC的中点,过点O的一直线分别与AB、CD交于点E、F , 连接BF交AC于点M , 连接DE、BO , 若∠COB=60°,FO=FC , 则下列结论:①FB⊥OC , OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB:OE=3:2,其中符合题意结论是 .
三、综合题
-
25. 如图,AB是 的直径,点D、E在 上,连接AE、ED、DA,连接BD并延长至点C,使得 .
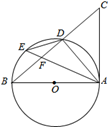 (1)、求证:AC是 的切线;(2)、若点E是的 中点,AE与BC交于点F,
(1)、求证:AC是 的切线;(2)、若点E是的 中点,AE与BC交于点F,①求证:CA=CF;
②若 的半径为3,BF=2,求AC的长.
26. 如图, 内接于 , 为直径,过点O作 ,交 的延长线于点F,交 于点D,E为 上一点,连接 ,其中 . (1)、求证:E是 的中点;(2)、求证: 是 的切线;(3)、如果 , ,求弦 的长.27. 如图1,在平面直角坐标系 中,函数 (m为常数, , )的图象经过点 和 ,直线 与x轴、y轴分别交于C,D两点.
(1)、求证:E是 的中点;(2)、求证: 是 的切线;(3)、如果 , ,求弦 的长.27. 如图1,在平面直角坐标系 中,函数 (m为常数, , )的图象经过点 和 ,直线 与x轴、y轴分别交于C,D两点. (1)、求 的度数;(2)、如图2,连接 、 ,当 时,求此时m的值;(3)、如图3,点A、点B分别是在x轴和y轴正半轴上的动点.再以 、 为邻边作矩形 .若点M恰好在函数 (m为常数, , )的图象上,且四边形 为平行四边形,求此时 、 的长度.28. 对于一个函数给出如下定义;对于函数y,若当 ,函数值y满足 ,且满足 ,则称此函数为“k属合函数”.例如:正比例函数 ,当 时, ,则 ,求得: ,所以函数 为“2属合函数”.(1)、一次函数 为“1属合函数”,求a的值.(2)、反比例函数 ,且 )是“k属合函数”,且 ,请求出 的值;(3)、已知二次函数 ,当 时,y是“k属合函数”,求k的取值范围.29. 定义:若抛物线L:y=ax2+bx+c的图象恒过定点M(x0 , y0),则称M(x0 , y0)为抛物线L的“不动点”.已知:若抛物线L:y=ax2﹣2ax+x+1(a<0);
(1)、求 的度数;(2)、如图2,连接 、 ,当 时,求此时m的值;(3)、如图3,点A、点B分别是在x轴和y轴正半轴上的动点.再以 、 为邻边作矩形 .若点M恰好在函数 (m为常数, , )的图象上,且四边形 为平行四边形,求此时 、 的长度.28. 对于一个函数给出如下定义;对于函数y,若当 ,函数值y满足 ,且满足 ,则称此函数为“k属合函数”.例如:正比例函数 ,当 时, ,则 ,求得: ,所以函数 为“2属合函数”.(1)、一次函数 为“1属合函数”,求a的值.(2)、反比例函数 ,且 )是“k属合函数”,且 ,请求出 的值;(3)、已知二次函数 ,当 时,y是“k属合函数”,求k的取值范围.29. 定义:若抛物线L:y=ax2+bx+c的图象恒过定点M(x0 , y0),则称M(x0 , y0)为抛物线L的“不动点”.已知:若抛物线L:y=ax2﹣2ax+x+1(a<0); (1)、求抛物线L的不动点坐标;(2)、已知平面直角坐标系中A(﹣1,0),B(1,0),C(3,0),以点B为圆心,OB为半径作⊙B,点P为⊙B上一点,将点C绕点P逆时针旋转90°得到点C',当点P为⊙B上运动时,求线段AC'长度的最大值;(3)、在(2)的条件下,若抛物线L的对称轴是直线x=2;
(1)、求抛物线L的不动点坐标;(2)、已知平面直角坐标系中A(﹣1,0),B(1,0),C(3,0),以点B为圆心,OB为半径作⊙B,点P为⊙B上一点,将点C绕点P逆时针旋转90°得到点C',当点P为⊙B上运动时,求线段AC'长度的最大值;(3)、在(2)的条件下,若抛物线L的对称轴是直线x=2;①求抛物线L的解析式;
②若直线PC交抛物线L于点E(x1 , y1)、F(x2 , y2),交y轴于点Q,平面内一点H坐标为H(4 ,2),记d=|x1﹣x2|,当点P在⊙B上运动时,求( )2的取值范围.
30. 如图1,在△ABC中,∠B=∠ACB=45°,AB=6 ,点D是BC上一点,作DE⊥AD交射线AC于E,DF平分∠ADE交AC于F.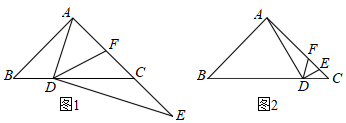 (1)、求证:AB•CF=BD•CD;(2)、如图2,当∠AED=75°时,求CF的长;(3)、若CD=3BD,求 .31. 规定:我们把一个函数关于某条直线或者某点作对称后形成的新函数,称之为原函数的“对称函数”.(1)、已知一次函数y=﹣2x+3的图象,求关于直线y=﹣x的对称函数的解析式;(2)、已知二次函数y=ax2+4ax+4a﹣1的图象为C1;
(1)、求证:AB•CF=BD•CD;(2)、如图2,当∠AED=75°时,求CF的长;(3)、若CD=3BD,求 .31. 规定:我们把一个函数关于某条直线或者某点作对称后形成的新函数,称之为原函数的“对称函数”.(1)、已知一次函数y=﹣2x+3的图象,求关于直线y=﹣x的对称函数的解析式;(2)、已知二次函数y=ax2+4ax+4a﹣1的图象为C1;①求C1关于点R(1,0)的对称函数图象C2的函数解析式;
②若两抛物线与y轴分别交于A、B两点,当AB=16时,求a的值;
(3)、若直线y=﹣2x﹣3关于原点的对称函数的图象上的存在点P,不论m取何值,抛物线y=mx2+(m﹣ )x﹣(2m﹣ )都不通过点P,求符合条件的点P坐标.32. (1)、(基础巩固)
(1)、(基础巩固)如图1,在 中, 为 上一点, .求证: .
(2)、(尝试应用)如图2,在 中, 为 上一点, 为 延长线上一点, ,若 , ,求 的长.
(3)、(拓展提高)如图3,在菱形 中, 是 上一点, 是 内一点, , , , , ,求菱形 的边长.
33. 如图,抛物线y=x2+bx+c与x轴交于A(一1,0),B(3,0)两点,过点A的直线l交抛物线于点C(2,m).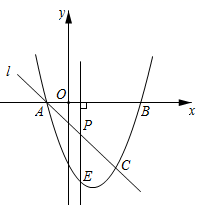 (1)、求抛物线的解析式.(2)、点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E,求线段PE最大时点P的坐标.(3)、点F是抛物线上的动点,在x轴上是否存在点D,使得以点A,C,D,F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.34. 定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形 中,若 , ,则称四边形 为准平行四边形.
(1)、求抛物线的解析式.(2)、点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E,求线段PE最大时点P的坐标.(3)、点F是抛物线上的动点,在x轴上是否存在点D,使得以点A,C,D,F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.34. 定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形 中,若 , ,则称四边形 为准平行四边形.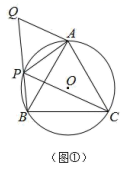

 (1)、如(图①), 、 、 、 是⊙O上的四个点, ,延长 到 ,使 .求证:四边形 是准平行四边形;(2)、如(图②),准平行四边形 内接于⊙O, , ,若⊙O的半径为5, ,求 的长;(3)、如(图③),在 中, , , ,若四边形 是准平行四边形,且 ,请直接写出 长的最大值.35. 在平面直角坐标系中,抛物线 ( )与 轴的两个交点分别为A、B,与 轴相交于点C,点A( ,0), ,连接BC,tan∠OCB=2.
(1)、如(图①), 、 、 、 是⊙O上的四个点, ,延长 到 ,使 .求证:四边形 是准平行四边形;(2)、如(图②),准平行四边形 内接于⊙O, , ,若⊙O的半径为5, ,求 的长;(3)、如(图③),在 中, , , ,若四边形 是准平行四边形,且 ,请直接写出 长的最大值.35. 在平面直角坐标系中,抛物线 ( )与 轴的两个交点分别为A、B,与 轴相交于点C,点A( ,0), ,连接BC,tan∠OCB=2. (1)、求该抛物线的解析式;(2)、设点P是抛物线上在第一象限内的动点(不与C、B重合),过点P做PD⊥BC,垂足为点D.
(1)、求该抛物线的解析式;(2)、设点P是抛物线上在第一象限内的动点(不与C、B重合),过点P做PD⊥BC,垂足为点D.①点P在运动过程中,线段PD的长度是否存在最大值?若存在,请求出点D的坐标;若不存在,请说明理由;
②以P、D、C为顶点的三角形与△COA相似时,求出点P的坐标.
36. 对于抛物线 ,我们将它的顶点以及它与 轴的两个交点构成的三角形称为该抛物线的“内接三角形”. (1)、下列抛物线,有“内接三角形”的是;(填序号)
(1)、下列抛物线,有“内接三角形”的是;(填序号)① ;② ;③
(2)、如图1,抛物线 与 轴的交点分别为点A、点B(点A在点B左边),顶点为点D,该抛物线的“内接三角形”△ABD为等边三角形.①求 的值;
②如图2,若该抛物线经过点(0,6),∠BAD的平分线交BD于点P,点M为射线AB上一点.连接直线PM交射线AD于点N,求 的值.
37. 如图,一次函数 的图象与反比例函数 的图象交于第一象限C(1,4)、D(4,m)两点,与坐标轴交于A、B两点,连接OC、OD(O是坐标原点).(1)、求△DOC的面积; (2)、将直线AB向下平移多少个单位长,直线与反比例函数图象只有1个交点?(3)、双曲线上是否存在一点P,使△POC与△POD的面积相等?若存在,请直接写出点P的坐标,若不存在,请说明理由.38. 阅读材料:各类方程的解法:
(2)、将直线AB向下平移多少个单位长,直线与反比例函数图象只有1个交点?(3)、双曲线上是否存在一点P,使△POC与△POD的面积相等?若存在,请直接写出点P的坐标,若不存在,请说明理由.38. 阅读材料:各类方程的解法:求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式,求解二元一次方程组,把它转化为一元一次方程来解;类似的,三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想——转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为 ,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
 (1)、问题:方程 的解是: =0, = , =;(2)、拓展:用“转化”思想求方程 的解;(3)、应用:如图,已知矩形草坪ABCD的长AD=21m,宽AB=8m,点P在AD上(AP>PD),小华把一根长为27m的绳子一段固定在点B,把长绳PB段拉直并固定在点P,再拉直,长绳的另一端恰好落在点C,求AP的长.39. 已知正方形ABCD中AC与BD交于点O , 点M在线段BD上,作直线AM交直线DC于点E , 过D作DH⊥AE于H , 设直线DH交AC于点N .
(1)、问题:方程 的解是: =0, = , =;(2)、拓展:用“转化”思想求方程 的解;(3)、应用:如图,已知矩形草坪ABCD的长AD=21m,宽AB=8m,点P在AD上(AP>PD),小华把一根长为27m的绳子一段固定在点B,把长绳PB段拉直并固定在点P,再拉直,长绳的另一端恰好落在点C,求AP的长.39. 已知正方形ABCD中AC与BD交于点O , 点M在线段BD上,作直线AM交直线DC于点E , 过D作DH⊥AE于H , 设直线DH交AC于点N .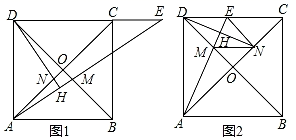 (1)、如图1,当M在线段BO上时,求证:OM=ON;(2)、如图2,当M在线段OD上,连接NE和MN , 当EN BD时,求证:四边形DENM是菱形;(3)、在(2)的条件下,若正方形边长为4,求EC的长.
(1)、如图1,当M在线段BO上时,求证:OM=ON;(2)、如图2,当M在线段OD上,连接NE和MN , 当EN BD时,求证:四边形DENM是菱形;(3)、在(2)的条件下,若正方形边长为4,求EC的长.