江苏省南通市如皋市2021届高三下学期数学5月第三次适应性考试试卷

试卷更新日期：2021-06-03 类型：高考模拟

进入出卷网下载

一、单选题

1. $\frac{1 - 2 i}{1 + i} + \frac{1 + 2 i}{1 - i}$ ＝（　　）

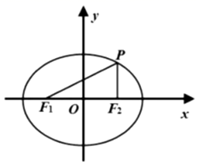
A、﹣1 B、﹣i C、1 D、i

查看试题解析
2. 已知随机变量 $X ~ N (1, σ^{2})$ ，若 $P (X \geq 0) = 0.6$ ，则 $P (X > 2) =$ （）

A、 $0.2$ B、 $0.4$ C、 $0.6$ D、 $0.8$

查看试题解析
3. 1943年深秋的一个夜晚，年仅19岁的曹火星在晋察冀边区创作了歌曲《没有共产党就没有中国》，毛主席得知后感觉歌名的逻辑上有点问题，遂提出修改意见，将歌名改成《没有共产党就没有新中国》，今年恰好是建党100周年，请问“没有共产党”是“没有新中国”的（）条件．

A、充分 B、必要 C、充分必要 D、既非充分又非必要

查看试题解析
4. 已知 $a = \log_{3} 5, b = {(\frac{1}{2})}^{\frac{1}{3}}, c = \log_{\frac{1}{3}} \frac{1}{6}$ ，则a，b，c的大小关系为（）

A、 $a > b > c$ B、 $b > a > c$ C、 $c > b > a$ D、 $c > a > b$

查看试题解析
5. ${(x^{2} + 3 x + 2)}^{5}$ 的展开式中 $x^{2}$ 的系数为（）

A、 $625$ B、 $800$ C、 $750$ D、 $600$

查看试题解析
6. 已知正三角形ABC的边长为3，且 $\vec{A P} = 2 \vec{P B} ， \vec{B Q} = 2 \vec{Q C} ， \vec{C R} = 2 \vec{R A}$ ，则 $\vec{P Q} \cdot \vec{P R}$ =（）

A、 $\frac{3}{2}$ B、 $\frac{3}{4}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
7. 已知椭圆 $\frac{x^{2}}{a_{1}^{2}} + y^{2} = 1$ 与双曲线 $\frac{x^{2}}{a_{2}^{2}} - y^{2} = 1$ 有相同的焦点 $F_{1}$ 、 $F_{2}$ ，设椭圆与双曲线的离心率分别为 $e_{1}$ 、 $e_{2}$ ，则（）

A、 $e_{1} e_{2} = 1$ B、 $e_{2}^{2} - e_{1}^{2} = 1$ C、 $e_{1}^{2} + e_{2}^{2} = 2 e_{1}^{2} e_{2}^{2}$ D、 $e_{2} = 2 e_{1}$

查看试题解析
8. 已知四棱锥 $P - A B C D$ 的侧面PAD为正三角形，底面ABCD为矩形，且面 $P A D ⊥$ 面ABCD，若 $P A = \frac{4 \sqrt{3}}{3} ， A B = 2$ ，则该四棱锥内可以放置最大的球的半径为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $2 - \sqrt{2}$ C、 $\frac{2 \sqrt{3}}{3}$ D、 $\frac{2}{3}$

查看试题解析

二、多选题

9. 已知 $a, b, c, d \in R$ ，则下列不等式一定成立的是（）

A、 $a^{2} b^{2} + c^{2} d^{2} \geq 2 a b c d$ B、 $a^{4} + b^{4} \geq a^{3} b + a b^{3}$ C、 ${(a b + c d)}^{2} \leq (a^{2} + c^{2}) (b^{2} + d^{2})$ D、 $\sqrt{a^{2} + b^{2}} + \sqrt{c^{2} + d^{2}} > \sqrt{{(a - c)}^{2}} + \sqrt{{(b - d)}^{2}}$

查看试题解析
10. 已知圆 $O : x^{2} + y^{2} = 4, A (1, 0), C (4, 0)$ ，点P在圆上且在第一象限内，则下列结论正确的是（）

A、 $P C = 2 P A$ B、 $∠ P C A \leq \frac{π}{6}$ C、 $∠ P A C > 2 ∠ P C A$ D、 $∠ P A C < 2 ∠ P C A$

查看试题解析
11. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，设与对角线 $A C_{1}$ 垂直的平面α截正方体表面所得截面多边形记为M，则关于多边形M的说法正确的是（）

A、M可能为正三角形 B、M可能为正方形 C、若M为六边形，则面积为定值 D、若M为六边形，则周长为定值

查看试题解析
12. 已知声音是由物体振动产生的声波．其中包含着正弦函数或余弦函数，而纯音的数学模型是函数 $y = A \sin ω t$ ，我们听到的声音是由纯音合成的，称之为复合音．若一个复合音的数学模型是函数 $f (x) = 2 \sin x - \sin 3 x$ ，则下列说法正确的是（）

A、 $π$ 是 $f (x)$ 的一个周期 B、 $f (x)$ 在 $[0 ， 2 π]$ 上有7个零点 C、 $f (x)$ 的最大值为3 D、 $f (x)$ 在 $[\frac{π}{6} ， \frac{π}{2}]$ 上是增函数

查看试题解析

三、填空题

13. 已知 $x ， y \in R^{+} ， x + 2 y = 1$ ，则 $\frac{1}{x} + \frac{x + y}{y}$ 的最小值为．

查看试题解析
14. 已知锐角 $△ A B C$ 中，角A，B，C的对边分别为a，b，c，现有下列四个判断：
甲： $a > b$ ；乙： $\sin A > \cos B$ ；丙： $\tan (A - B) > 0$ ；丁： $\cos A < \cos B$ ．

若上述四个论断有且只有一个是正确的，那么正确的是．

查看试题解析
15. 已知圆周上等距离的排列着八个点 $A_{1} ， A_{2} ， \dots ， A_{8}$ ，现从中任取三个不同的点作为一个三角形的三个顶点，则恰好能构成一个直角三角形的概率为．

查看试题解析
16. 已知函数 $f (x) = \sum_{i = 1}^{2021} | x - i |$ ，则当 $x = x_{0}$ 时，函数 $f (x)$ 有最小值，则 $x_{0} =$ ．此时 $g (x_{0}) = \sum_{i = 1}^{2021} (x_{0} - i) =$ ．

查看试题解析

四、解答题

17. 已知 $△ A B C$ 中， $B = \frac{π}{3}, A C = \sqrt{13}$ ， ▲ ，求 $S_{△ A B C}$ ．
请从① $\sin A = 4 \sin C$ ；② $a - c = 3$ ；③ $\cos C = \frac{7}{26} \sqrt{13}$ 三个条件中选择一个补充在上面问题中，并作答．

查看试题解析
18. 已知数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，若 $a_{1} = 1, 2 S_{n} = a_{n} a_{n + 1}$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} = \frac{a_{n} + a_{n + 1}}{a_{n}^{2} a_{n + 1}^{2}}$ ，求数列 ${b_{n}}$ 的前n项和 $T_{n}$ ．

查看试题解析
19. 某空调商家，对一次性购买两台空调的客户推出两种质保期两年内的保维修方案：
方案一：交纳质保金300元，在质保的两年内两条空调共可免费维修2次，超过2次每次收取维修费200元．

方案二：交纳质保金400元，在质保的两年内两台空调共可免费维修3次，超过3次每次收取维修费200元．

小李准备一次性购买两台这种空调，现需决策在购买时应购买哪种质保方案，为此搜集并整理了100台这种空调质保期内两年内维修的次数，统计得下表：

维修次数

0

1

2

3

空调台数

20

30

30

20

用以上100台空调维修次数的频率代替一台机器维修次数发生的概率．

(1)、求购买这样的两台空调在质保期的两年内维修次数超过2次的概率；

(2)、请问小李选择哪种质保方案更合算．

查看试题解析
20. 如图，在三棱台 $A B C - D E F$ 中， $C F ⊥$ 面DEF， $A B ⊥ B C$ ， $A B = B C = \frac{1}{2} E F = \frac{1}{2} C F = 2$ ．

(1)、若 $\vec{C P} = 2 \vec{B P}$ ，证明：面 $P D F ⊥$ 面CDE；

(2)、求二面角 $A - C E - D$ 的余弦值．

查看试题解析
21. 已知椭圆 $C ： \cdot \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b ， 0 < b < 2)$ 的左、右焦点分别为 $F_{1} ， F_{2}$ ，点P在椭圆上， $P F_{2} ⊥ F_{1} F_{2}$ ．若 $△ P F_{1} F_{2}$ 的周长为6，面积为 $\frac{3}{2}$ ．

(1)、求椭圆C的标准方程；

(2)、已知椭圆的左、右顶点分别为A，B，过 $(\frac{1}{2} ， 0)$ 直线与椭圆交于M，N两点，设直线AM，BN的斜率分别为 $k_{1} ， k_{2}$ ，证明： $\frac{k_{1}}{k_{2}}$ 为定值．

查看试题解析
22. 已知函数 $f (x) = x + \frac{1}{x} ， g (x) = 2 + {(\ln x)}^{2}$ ．

(1)、证明：两函数图象有且只有一个公共点；

(2)、证明： $\sum_{k = 1}^{n} \sqrt{\frac{k + 1}{k}} - \sum_{k = 1}^{n} \sqrt{\frac{k}{k + 1}} > \ln (n + 1) (n \in e N^{*})$ ．

查看试题解析

维修次数	0	1	2	3
空调台数	20	30	30	20