广东省汕头市2021届高三数学三模试卷

试卷更新日期：2021-06-03 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知复数 $z = \sqrt{3} + i$ ， $\bar{z}$ 是z的共轭复数， $z_{0} = \frac{\bar{z}}{z}$ ， $z_{0}$ 在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知全集 $U = R$ ，集合 $A = {y | y = x^{2} + 2}$ ，集合 $B = {x | 9 - x^{2} > 0}$ ，则阴影部分表示的集合为（）

A、 $[- 3 ， 2]$ B、 $(- 3 ， 2)$ C、 $(- 3 ， 2]$ D、 $[- 3 ， 2)$

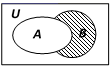查看试题解析
3. 现有红、黄、蓝、绿、紫五只杯子，将它们叠成一叠，则在黄色杯子和绿色杯子相邻的条件下，黄色杯子和红色杯子也相邻的概率为（）

A、 $\frac{1}{10}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
4. 已知 $S_{n}$ 是数列 ${a_{n}}$ 的前n项和，则“ $S_{n + 1} + 2 S_{n - 1} = 3 S_{n}$ 对 $n \geq 2$ 恒成立”是“ ${a_{n}}$ 是公比为2的等比数列”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 已知 $f (x)$ 是定义在R上的函数，满足 $\forall x \in R$ .都有 $f (x) = f (- x)$ ，且在 $[0 ， + \infty)$ 上单调递增.若 $a = f (\frac{1}{2})$ ， $b = f (\sin 1)$ ， $c = f (\cos 2)$ ，则a，b，c的大小关系为（）

A、 $a > b > c$ B、 $b > a > c$ C、 $a > c > b$ D、 $c > a > b$

查看试题解析
6. 区块链作为一种革新的技术，已经被应用于许多领域，包括金融､政务服务､供应链､版权和专利､能源､物联网等.在区块链技术中，若密码的长度设定为256比特，则密码一共有 $2^{256}$ 种可能，因此，为了破解密码，最坏情况需要进行 $2^{256}$ 次哈希运算.现在有一台机器，每秒能进行 $2.5 \times 10^{11}$ 次哈希运算，假设机器一直正常运转，那么在最坏情况下，这台机器破译密码所需时间大约为（）(参考数据 $\lg 2 \approx 0.3010$ ， $\lg 3 \approx 0.4771$ )

A、 $4.5 \times 10^{73}$ 秒 B、 $4.5 \times 10^{65}$ 秒 C、 $4.5 \times 10^{7}$ 秒 D、28秒

查看试题解析
7. 设 $F$ 是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ 的右焦点，双曲线两渐近线分别为 $l_{1}$ ， $l_{2}$ ，过点 $F$ 作直线 $l_{1}$ 的垂线，分别交 $l_{1}$ ， $l_{2}$ 于 $A$ ， $B$ 两点，若 $A$ ， $B$ 两点均在 $x$ 轴上方且 $| O A | = 3$ ， $| O B | = 5$ ，则双曲线的离心率e为（）

A、 $\frac{\sqrt{5}}{2}$ B、2 C、 $\sqrt{5}$ D、 $\sqrt{6}$

查看试题解析
8. 已知定义在R上的函数 $f (x)$ 的导函数为 $f' (x)$ ，且满足 $f' (x) - f (x) > 0$ ， $f (2021) = e^{2021}$ ，则不等式 $f (\frac{1}{e} \ln x) < \sqrt[e]{x}$ 的解集为（）

A、 $(e^{2021} ， + \infty)$ B、 $(0 ， e^{2021})$ C、 $(e^{2021 e} ， + \infty)$ D、 $(0 ， e^{2021 e})$

查看试题解析

二、多选题

9. 为响应国家号召，打赢脱贫致富攻坚战，某贫困村主要产业是种植蜜柚，由于销售渠道单一，导致蜜柚滞销或低价出售.其定点扶贫单位为帮助该村真正脱贫，为该村建立多种销售渠道，一年后该村的蜜柚销售收入增加了一倍，实现翻番.为更好地了解该村的蜜柚销售收入变化情况，统计了该村扶贫前后的蜜柚销售收入构成比例，得到如下饼图：

则下面结论中正确的是（）

A、扶贫后，该村的城乡集贸市场销售渠道的收入减少； B、扶贫后，该村的自媒体销售渠道的收入增加了一倍以上； C、扶贫后，该村的农产品批发市场销售渠道的收入增加了一倍； D、扶贫后，该村的农产品电商销售渠道收入是扶贫前的四倍.

查看试题解析
10. 已知函数 $f (x) = a \sin x + b \cos x (a b \neq 0)$ ，且对任意 $x \in R$ 都有 $f (\frac{π}{6} - x) = f (\frac{π}{6} + x)$ ，则以下正确的有（）

A、 $f (x)$ 的最小正周期为 $2 π$ B、 $f (x)$ 在 $[\frac{π}{6} ， \frac{7 π}{6}]$ 上单调递减 C、 $x = \frac{2 π}{3}$ 是 $f (x)$ 的一个零点 D、 $\frac{a}{b} = \frac{\sqrt{3}}{3}$

查看试题解析
11. 如图，正方体ABCD﹣A₁B₁C₁D₁的棱长为a，线段B₁D₁上有两个动点E，F，且EF $= \frac{\sqrt{2}}{2}$ a，以下结论正确的有（）

A、AC⊥BE B、点A到△BEF的距离为定值 C、三棱锥A﹣BEF的体积是正方体ABCD﹣A₁B₁C₁D₁体积的 $\frac{1}{12}$ D、异面直线AE，BF所成的角为定值

查看试题解析
12. 画法几何的创始人——法国数学家加斯帕尔·蒙日发现：与椭圆相切的两条垂直切线的交点的轨迹是以椭圆中心为圆心的圆，我们通常把这个圆称为该椭圆的蒙日圆.已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{2}}{2}$ ， $F_{1} ， F_{2}$ 分别为椭圆的左､右焦点， $A ， B$ 为椭圆上两个动点.直线l的方程为 $b x + a y - a^{2} - b^{2} = 0$ .下列说法正确的是（）

A、C的蒙日圆的方程为 $x^{2} + y^{2} = 3 b^{2}$ B、对直线l上任意点P， $\vec{P A} \cdot \vec{P B} > 0$ C、记点A到直线l的距离为 $d$ ，则 $d - | A F_{2} |$ 的最小值为 $\frac{4 \sqrt{3}}{3} b$ D、若矩形 $M N G H$ 的四条边均与C相切，则矩形 $M N G H$ 面积的最大值为 $6 b^{2}$

查看试题解析

三、填空题

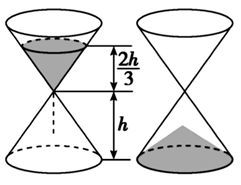
13. 函数 $y = a^{x - 3} + 1$ （ $a > 0$ 且 $a \neq 1$ ）的图象恒过定点A，若点A在直线 $m x + n y - 1 = 0$ 上，其中 $m > 0$ ， $n > 0$ ，则mn的最大值为.

查看试题解析
14. 已知非零向量 $\vec{a}, \vec{b}$ 满足 $| \vec{a} | = 2 | \vec{b} |$ ，且 $(\vec{a} - \vec{b}) ⊥ \vec{b}$ ，则 $\vec{a}$ 与 $\vec{b}$ 的夹角为．

查看试题解析
15. 沙漏是古代的一种计时装置，它由两个形状完全相同的容器和一个狭窄的连接管道组成，开始时细沙全部在上部容器中，细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时，如图，某沙漏由上下两个圆锥组成，圆锥的底而直径和高均为10cm，细沙全部在上部时，其高度为圆锥高度的 $\frac{2}{3}$ （细管长度忽略不计）.若细沙全部漏入下部后，恰好堆成一个盖住沙漏底部的圆锥形沙堆，则此锥形沙堆的高度为.（精确到0. 01cm）.

查看试题解析
16. 已知数列 ${a_{n}}$ 满足 $a_{1} + 3 a_{2} + 5 a_{3} + \dots + (2 n - 1) a_{n} = 3^{n}$ ，则 $a_{3} =$ ，若对任意的 $n \in N^{*}$ ， $a_{n} \geq {(- 1)}^{n} λ$ 恒成立，则 $λ$ 的取值范围为.

查看试题解析

四、解答题

17. 在① ${(\sin B + \sin C)}^{2} = \sin^{2} A + 3 \sin B \sin C$ ，② $2 c = 2 a \cos B + b$ ，③ $b \cos C + c \cos B - 2 a \cos A = 0$ 这三个条件中任选一个，补充到下面问题中，并解答问题.在 $△ A B C$ 中，内角A，B，C的对边长分别为a，b，c，且 .

(1)、求角A的大小；

(2)、若 $△ A B C$ 是锐角三角形，且 $b = 2$ ，求边长c的取值范围.
（注：如果选择多个条件分别解答，则按第一个解答计分）

查看试题解析
18. 已知数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，数列 ${\frac{S_{n}}{n}}$ 是首项为 $\frac{1}{2}$ ，公差为 $\frac{1}{4}$ 的等差数列，若 $[x]$ 表示不超过x的最大整数，如 $[0.5] = 0$ ， $[\lg 499] = 2$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} = [\lg a_{n}]$ ，求数列 ${b_{n}}$ 的前2020项的和.

查看试题解析
19. 已知 $△ A B C$ 是正三角形，线段 $A E$ 和 $C D$ 都垂直于平面 $A B C$ ，且 $A E = 2 C D = 2$ ， $F$ 为 $B E$ 的中点，设平面 $B D E \cap$ 平面 $A B C = l$ .

(1)、求证： $D F // l$ ；

(2)、当平面 $B D E$ 与平面 $A B C$ 所成的锐二面角为 $\frac{π}{4}$ 时，求几何体 $A B C D E$ 的体积.

查看试题解析
20. 已知圆 $C ： x^{2} + {(y - 2)}^{2} = 1$ 与定直线 $l ： y = - 1$ ，且动圆 $M$ 与圆 $C$ 外切并与直线 $l$ 相切.

(1)、求动圆圆心M的轨迹E的方程；

(2)、已知点P是直线 $l_{1} ： y = - 2$ 上一个动点，过点P作轨迹E的两条切线，切点分别为A、B.
①求证：直线AB过定点；

②求证： $∠ P C A = ∠ P C B$ .

查看试题解析
21. 第13届女排世界杯于2019年9月14日在日本举行，共有12支参赛队伍，本次比赛启用了新的排球用球，MIKSA-V200W，已知这种球的质量指标ξ（单位：g）服从正态分布N（270，5²）.比赛赛制采取单循环方式，即每支球队进行11场比赛（采取5局3胜制），最后靠积分取得最后冠军，积分规则如下：比赛中以3：0或3：1取胜的球队积3分，负队积0分；而在比赛中以3：2取胜的球队积2分，负队积1分.已知第10轮中国队对抗塞尔维亚队，设每局比赛中国队取胜的概率为 $p (0 < p < 1)$

(1)、若比赛准备了1000个排球，请估计质量指标在（260，265]内的排球个数（计算结果取整数）.

(2)、第10轮比赛中，记中国队3：1取胜的概率为 $f (p)$ .
（i）求出 $f (p)$ 的最大值点 $p_{0}$ ；

（ii）若以 $p_{0}$ 作为p的值，记第10轮比赛中，中国队所得积分为X，求X的分布列及数学期望.

参考数据：若 $X ~ N (μ ， σ^{2})$ ，则 $p (μ - σ < X < μ + σ) \approx 0.6826$ ， $p (μ - 2 σ < X < μ + 2 σ) \approx 0.9544$

查看试题解析
22. 已知函数 $f (x) = e^{x} - \frac{1}{2} x^{2} - a x - 1$ ， $g (x) = \cos x + \frac{1}{2} x^{2} - 1$ .

(1)、当 $a = 1$ 时，求证：当 $x \geq 0$ 时， $f (x) \geq 0$ ；

(2)、若 $f (x) + g (x) \geq 0$ 在 $[0 ， + \infty)$ 上恒成立，求a的取值范围.

查看试题解析