初中数学人教版八年级下学期期末考试复习专题:03勾股定理
试卷更新日期:2021-06-03 类型:复习试卷
一、单选题
-
1. 在直角三角形中,若两条边的长分别是1cm、2cm,则第三边的长为( )A、3cm B、 cm C、2cm或 cm D、 cm或 cm2. 在△ABC中,∠A,∠B,∠C的对边分别是a、b、c,下列说法错误的是( )A、如果∠C-∠B=∠A,则△ABC是直角三角形 B、如果c2=b2-a2 , 则△ABC是直角三角形 C、如果∠A:∠B:∠C=1:2:3,则△ABC是直角三角形 D、如果a2+b2≠c2 , 则△ABC不是直角三角形3. 如图1,分别以直角三角形三边为边向外作正方形,面积分别为 , , ;如图2,分别以直角三角形三边长为直径向外作半圆,面积分别为 , , .其中 , , , ,则 ( )
 A、10 B、9 C、8 D、74. 下列四组线段中,不能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,5. 已知一个直角三角形三边的平方和为800,则这个直角三角形的斜边长为( )A、20 B、40 C、80 D、1006. 如图所示,一个圆柱体高8 cm , 底面半径2 cm , 一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程 取 是( )
A、10 B、9 C、8 D、74. 下列四组线段中,不能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,5. 已知一个直角三角形三边的平方和为800,则这个直角三角形的斜边长为( )A、20 B、40 C、80 D、1006. 如图所示,一个圆柱体高8 cm , 底面半径2 cm , 一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程 取 是( )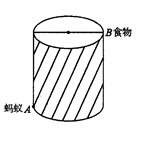 A、20cm B、10cm C、14cm D、无法确定7. 等腰三角形一腰长为5,这一腰上的高为3,则这个等腰三角形底边长为( )A、 B、 C、 或 D、4或8. 如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边长是5,小正方形的边长是7,则大正方形的面积是( )
A、20cm B、10cm C、14cm D、无法确定7. 等腰三角形一腰长为5,这一腰上的高为3,则这个等腰三角形底边长为( )A、 B、 C、 或 D、4或8. 如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边长是5,小正方形的边长是7,则大正方形的面积是( )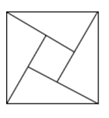 A、121 B、144 C、169 D、1969. 直角三角形的两条直角边为a、b,斜边为c,斜边上的高为h,下列结论:①a2+b2=c2;②ab=ch;③ .其中正确的是( )A、①②③ B、① C、①② D、①③10. 在△ABC中,三边长分别为a、b、c,且a+c=2b,c-a= b,则△ABC是( )A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形
A、121 B、144 C、169 D、1969. 直角三角形的两条直角边为a、b,斜边为c,斜边上的高为h,下列结论:①a2+b2=c2;②ab=ch;③ .其中正确的是( )A、①②③ B、① C、①② D、①③10. 在△ABC中,三边长分别为a、b、c,且a+c=2b,c-a= b,则△ABC是( )A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形二、填空题
-
11. 如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A、C、D的面积依次为4、6、18,则正方形B的面积为
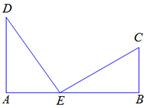
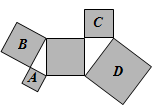 12. 如下图,在四边形ABCD中, , , , ,且 ,则四边形ABCD的面积为 .
12. 如下图,在四边形ABCD中, , , , ,且 ,则四边形ABCD的面积为 .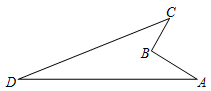 13. 如图, 的直角边 , , 在数轴上,在 上截取 ,以原点 为圆心, 为半径画弧,交边 于点 ,则点 对应的实数是 .
13. 如图, 的直角边 , , 在数轴上,在 上截取 ,以原点 为圆心, 为半径画弧,交边 于点 ,则点 对应的实数是 . 14. 如图,在四边形ABCD中,AB=1,BC=1,CD=2, 则四边形ABCD的面积是 .
14. 如图,在四边形ABCD中,AB=1,BC=1,CD=2, 则四边形ABCD的面积是 .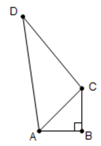 15. 如图,∠OAB=∠OBC=∠OCD=90°,AB=BC=CD=1,OA=2,则OD2= .
15. 如图,∠OAB=∠OBC=∠OCD=90°,AB=BC=CD=1,OA=2,则OD2= .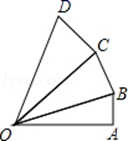 16. 我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的图形就用了这种分割方法若 ,正方形ODCE的边长为1,则BD等于 .
16. 我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的图形就用了这种分割方法若 ,正方形ODCE的边长为1,则BD等于 .
三、解答题
-
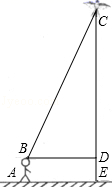
17. 身高1.6米的小明想利用“勾股定理”测得下图风筝CE的高度,于是他测得BD的长度为25米,并根据手中剩余线的长度计算出风筝线BC的长为65米.求风筝的高度CE.