2021年高考理数押题密卷B(新课标III卷)
试卷更新日期:2021-06-03 类型:高考模拟
一、选择题:本题共12小题,每小题5分,共60分。
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 若复数 满足 ,则 ( )A、 B、 C、1 D、53. 已知样本数据为 ,该样本平均数为 ,方差为 ,现加入一个数 ,得到新样本的平均数为 ,方差为 ,则( )A、 B、 C、 D、4. 某大型建筑工地因施工噪音过大,被周围居民投诉.现环保局要求其整改,降低声强.已知声强 (单位: ))表示声音在传播途径中每平方米面积上的声能流密度,声强级 (单位: )与声强 的函数关系式为 ,其中 为正实数.已知 时, .若整改后的施工噪音的声强为原声强的 ,则整改后的施工噪音的声强级降低了( )A、 B、 C、 D、5. 设 、 分别为双曲线 的左、右焦点,若在双曲线右支上存在点 ,满足 ,且 到直线 的距离等于双曲线的实轴长,则该双曲线的离心率 为( )A、 B、 C、 D、6. 若非零向量 满足 , ,则 与 的夹角为( )A、 B、 C、 D、7. 在 中,内角 、B、 所对的边分别为 、b、 ,若角 、C、 成等差数列,角 的角平分线交 于点 ,且 , ,则 的值为( )A、3 B、 C、 D、8. 如图,小方格是边长为1的小正方形,粗线画出的是某四棱锥的三视图,则该四棱锥的外接球表面积为( )
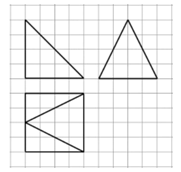 A、32π B、 C、41π D、9. 已知函数 满足 ,且 的最小值为 ,则 的值为( )A、 B、1 C、 D、210. 已知曲线 在 , ,两点处的切线分别与曲线 相切于 , ,则 的值为( )A、1 B、2 C、 D、11. 抛物线 的焦点为F,点 为该抛物线上的动点,点A是抛物线的准线与坐标轴的交点,则 的最大值是( )A、2 B、 C、 D、12. 已知函数 有两个零点 ,且存在唯一的整数 ,则实数 的取值范围是( )A、 B、 C、 D、
A、32π B、 C、41π D、9. 已知函数 满足 ,且 的最小值为 ,则 的值为( )A、 B、1 C、 D、210. 已知曲线 在 , ,两点处的切线分别与曲线 相切于 , ,则 的值为( )A、1 B、2 C、 D、11. 抛物线 的焦点为F,点 为该抛物线上的动点,点A是抛物线的准线与坐标轴的交点,则 的最大值是( )A、2 B、 C、 D、12. 已知函数 有两个零点 ,且存在唯一的整数 ,则实数 的取值范围是( )A、 B、 C、 D、二、填空题:本题共4小题,每小题5分,共20分。
-
13. 已知实数 , 满足 ,则 的最小值为 .14. 的展开式中的常数项为 .15. 设圆锥的顶点为 , 为圆锥底面圆 的直径,点 为圆 上的一点(异于 、 ),若 ,三棱锥 的外接球表面积为 ,则圆锥的体积为.16. 已知 , 在 上恒成立,则实数 的取值范围为 .
三、解答题:共70分。 (一)必考题:共60分。
-
17. 已知 数列满足 , .(1)、证明:数列 为等差数列.(2)、求数列 的前 项和.18. 2020年是决胜全面建成小康社会、决战脱贫攻坚之年,面对新冠肺炎疫情和严重洪涝灾害的考验.党中央坚定如期完成脱贫攻坚目标决心不动摇,全党全社会戮力同心真抓实干,取得了积极成效.某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积x与相应的管理时间y的关系如下表所示:
土地使用面积 (单位:亩)
1
2
3
4
5
管理时间 (单位:月)
8
10
14
24
23
并调查了某村 300 名村民参与管理的意愿,得到的部分数据如下表所示;
愿意参与管理
不愿意参与管理
男性村民
140
60
女性村民
40
参考公式:
参考数据:
(1)、做出散点图,判断土地使用面积 与管理时间 是否线性相关;并根据相关系数 说明相关关系的强弱.(若 ,认为两个变量有很强的线性相关性, r值精确到0.001).(2)、若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,且每位村民参与管理的意互不影响,则从该贫困县村民中任取3人,记取到不愿意参与管理的女性村民的人数为 ,求 的分布列及数学期望.19. 如图所示,直角梯形 中, , , ,四边形EDCF为矩形, ,平面 平面 .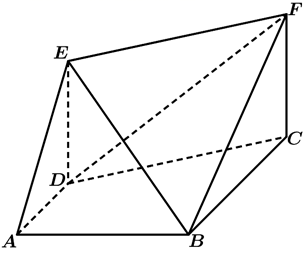 (1)、求证: 平面 ;(2)、求平面 与平面 所成锐二面角的余弦值.20. 已知椭圆 ,其上顶点与左右焦点 围成的是面积为 的正三角形.(1)、求椭圆 的方程;(2)、过椭圆 的右焦点 的直线 ( 的斜率存在)交椭圆 于 两点,弦 的垂直平分线交 轴于点 ,问: 是否是定值?若是,求出定值:若不是,说明理由.21. 已知函数 , .(1)、讨论函数 的单调性;(2)、若 ,求 的值;(3)、证明: .
(1)、求证: 平面 ;(2)、求平面 与平面 所成锐二面角的余弦值.20. 已知椭圆 ,其上顶点与左右焦点 围成的是面积为 的正三角形.(1)、求椭圆 的方程;(2)、过椭圆 的右焦点 的直线 ( 的斜率存在)交椭圆 于 两点,弦 的垂直平分线交 轴于点 ,问: 是否是定值?若是,求出定值:若不是,说明理由.21. 已知函数 , .(1)、讨论函数 的单调性;(2)、若 ,求 的值;(3)、证明: .四、(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。[选修4-4:坐标系与参数方程]