山西省吕梁市2021届高三理数三模试卷
试卷更新日期:2021-06-01 类型:高考模拟
一、单选题
-
1. 已知集合 ,集合 ,则 ( )A、 B、 C、 D、2. 若复数 满足 , ,则 在复平面内对应的点为( )A、 B、 C、 D、3. 北斗导航系统由55颗卫星组成,于2020年6月23日完成全球组网部署,全面投入使用.北斗七星自古是我国人民辨别方向判断季节的重要依据,北斗七星分别为天枢、天璇、天玑、天权、玉衡、开阳、摇光,其中玉衡最亮,天权最暗.一名天文爱好者从七颗星中随机选两颗进行观测,则玉衡和天权至少一颗被选中的概率为( )
 A、 B、 C、 D、4. 已知 , , ,若 ,则向量 , 夹角的正切值为( )A、 B、1 C、 D、5. 已知点 为直线 : 上一点,点 为圆 : 上一点,则 的最小值为( )A、 B、 C、1 D、6. 设 , ,化简 ( )A、 B、 C、 D、7. 已知函数 ,若 的图象过点 ,相邻对称轴的距离为 ,则 的解析式可能为( )A、 B、 C、 D、8. 的展开式中 的系数为( )A、88 B、104 C、 D、9. 函数 的部分图象大致为( )A、
A、 B、 C、 D、4. 已知 , , ,若 ,则向量 , 夹角的正切值为( )A、 B、1 C、 D、5. 已知点 为直线 : 上一点,点 为圆 : 上一点,则 的最小值为( )A、 B、 C、1 D、6. 设 , ,化简 ( )A、 B、 C、 D、7. 已知函数 ,若 的图象过点 ,相邻对称轴的距离为 ,则 的解析式可能为( )A、 B、 C、 D、8. 的展开式中 的系数为( )A、88 B、104 C、 D、9. 函数 的部分图象大致为( )A、 B、
B、 C、
C、 D、
D、 10. 已知如图,在棱长为2的正方体 中,过 且与 平行的平面交 于点 ,则 ( )
10. 已知如图,在棱长为2的正方体 中,过 且与 平行的平面交 于点 ,则 ( ) A、2 B、 C、 D、111. 已知抛物线 : 的焦点为 ,过点 的直线交 于 , 两点, 的重心为点 ,则点 到直线 的距离的最小值为( )A、2 B、 C、 D、12. 已知函数 满足 ,且 时, ,若 时,方程 有三个不同的根,则 的取值范围为( )A、 B、 C、 D、
A、2 B、 C、 D、111. 已知抛物线 : 的焦点为 ,过点 的直线交 于 , 两点, 的重心为点 ,则点 到直线 的距离的最小值为( )A、2 B、 C、 D、12. 已知函数 满足 ,且 时, ,若 时,方程 有三个不同的根,则 的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 若变量 , 满足约束条件 ,则 的最小值为.14. 已知双曲线 : , ,过点 的直线交 于 , 两点, 为 的中点,且直线 与 的一条渐近线垂直,则 的离心率为.15. 已知锐角 中, , , ,延长 到点 ,使 ,则 .
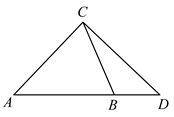 16. 如图所示的三棱锥 , 平面 , ,若 , , , ,当 取最大值时,点 到平面 的距离为.
16. 如图所示的三棱锥 , 平面 , ,若 , , , ,当 取最大值时,点 到平面 的距离为.
三、解答题
-
17. 已知正项等比数列 的前 项和为 ,若 , , 成等差数列, .
(Ⅰ)求 与 ;
(Ⅱ)设 ,数列 的前 项和记为 ,求 .
18. 如图,四边形 为正方形, 平面 , 为等腰三角形, , .
(Ⅰ)求证: 平面 ;
(Ⅱ)求二面角 的平面角的余弦值.
19. 核酸检测也就是病毒DNA和RNA的检测,是目前病毒检测最先进的检验方法,在临床上主要用于新型冠状乙肝、丙肝和艾滋病的病毒检测.通过核酸检测,可以检测血液中是否存在病毒核酸,以诊断机体有无病原体感染.某研究机构为了提高检测效率降低检测成本,设计了如下试验,预备12份试验用血液标本,其中2份阳性,10份阴性,从标本中随机取出n份分为一组,将样本分成若干组,从每一组的标本中各取部分,混合后检测,若结果为阴性,则判定该组标本均为阴性,不再逐一检测;若结果为阳性,需对该组标本逐一检测.以此类推,直到确定所有样本的结果.若每次检测费用为a元,记检测的总费用为 元.(1)、当 时,求 的分布列和数学期望;(2)、(ⅰ)比较 与 两种方案哪一个更好,说明理由;(ⅱ)试猜想100份标本中有2份阳性,98份阴性时, 和 两种方案哪一个更好(只需给出结论不必证明).
20. 已知椭圆 : 上有一点 ,点 在 轴上方, , 分别为 的左,右焦点,当△ 的面积取最大值 时, .(1)、求 的标准方程;(2)、若直线 交 于 , 两点,设 中点为 , 为坐标原点, ,作 ,求证: 为定值.