陕西省西安市灞桥区2021年数学中考一模试卷
试卷更新日期:2021-06-01 类型:中考模拟
一、单选题
-
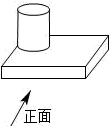
1. 计算: ( )A、1 B、0 C、2020 D、﹣20202. 如图,几何体的左视图是( )
 A、
A、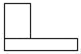 B、
B、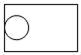 C、
C、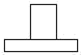 D、
D、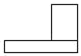 3. 如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )A、相等 B、互余或互补 C、互补 D、相等或互补4. 已知正比例函数y=3x,若该正比例函数图象经过点(a,4a﹣1),则a的值为( )A、1 B、﹣1 C、 D、﹣5. 下列运算结果正确的是( )A、(a2)3=a5 B、(a﹣b)2=a2﹣b2 C、﹣3a2b﹣2a2b=﹣a2b D、﹣a2b÷a2=﹣b6. 在平面直角坐标系中,将一次函数 的图象沿x轴向左平移m(m≥0)个单位后经过原点O,则m的值为( )A、 B、 C、2 D、7. 如图,在矩形ABCD中,AB=10,P是CD边上一点,M、N、E分别是PA、PB、AB的中点,以下四种情况,哪一种四边形PMEN不可能为矩形( )
3. 如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )A、相等 B、互余或互补 C、互补 D、相等或互补4. 已知正比例函数y=3x,若该正比例函数图象经过点(a,4a﹣1),则a的值为( )A、1 B、﹣1 C、 D、﹣5. 下列运算结果正确的是( )A、(a2)3=a5 B、(a﹣b)2=a2﹣b2 C、﹣3a2b﹣2a2b=﹣a2b D、﹣a2b÷a2=﹣b6. 在平面直角坐标系中,将一次函数 的图象沿x轴向左平移m(m≥0)个单位后经过原点O,则m的值为( )A、 B、 C、2 D、7. 如图,在矩形ABCD中,AB=10,P是CD边上一点,M、N、E分别是PA、PB、AB的中点,以下四种情况,哪一种四边形PMEN不可能为矩形( ) A、AD=3 B、AD=4 C、AD=5 D、AD=68. 如图,AB为⊙O的直径,C,D为⊙O上的点, = .若∠CBA=40°,则∠CBD的大小为( )
A、AD=3 B、AD=4 C、AD=5 D、AD=68. 如图,AB为⊙O的直径,C,D为⊙O上的点, = .若∠CBA=40°,则∠CBD的大小为( )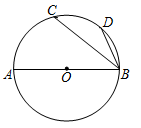 A、50° B、40° C、25° D、20°9. 将抛物线y=x2向左平移4个单位后,再向下平移2个单位,则所得到的抛物线的解析式为( )A、y=(x+4)2+2 B、y=(x+4)2﹣2 C、y=(x﹣4)2+2 D、y=(x﹣4)2﹣210. 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
A、50° B、40° C、25° D、20°9. 将抛物线y=x2向左平移4个单位后,再向下平移2个单位,则所得到的抛物线的解析式为( )A、y=(x+4)2+2 B、y=(x+4)2﹣2 C、y=(x﹣4)2+2 D、y=(x﹣4)2﹣210. 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
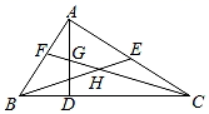 A、①②③④ B、①②③ C、②④ D、①③
A、①②③④ B、①②③ C、②④ D、①③二、填空题
-
11. 写出一个比 大的无理数:.12. 一个多边形的每一个外角都等于30°,则这个多边形的边数是 .13. 如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,m),C(3,m+6),那么图象同时经过点B与点D的反比例函数表达式为.
 14. 如图所示,四边形OABC是正方形,边长为4,点A、C分别在x轴、y轴的正半轴上,点D在OA上,且D点的坐标为(1,0),P是OB上一动点,则PA+PD的最小值为.
14. 如图所示,四边形OABC是正方形,边长为4,点A、C分别在x轴、y轴的正半轴上,点D在OA上,且D点的坐标为(1,0),P是OB上一动点,则PA+PD的最小值为.
三、解答题
-
15. 计算:( )﹣1﹣2tan45°+4sin60°﹣2 .16. 计算: .17. 如图,请用尺规作图法,在矩形ABCD的边BC和AD上分别找一点E、F使得四边新AECF为菱形.(保留作图痕迹,不写作法)
 18. 如图,△ABD和△BCE都是等边三角形,∠ABC<105°,AE与DC交于点F.
18. 如图,△ABD和△BCE都是等边三角形,∠ABC<105°,AE与DC交于点F. (1)、求证:AE=DC;(2)、求∠BFE的度数;(3)、若AF=9.17cm,BF=1.53cm,CF=7.53cm,求CD.19. 某学校为了丰富学生课余生活,开展了“第二课堂”活动,推出了以下四种选修课程: .绘画; .唱歌; .跳舞; .演讲; .书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
(1)、求证:AE=DC;(2)、求∠BFE的度数;(3)、若AF=9.17cm,BF=1.53cm,CF=7.53cm,求CD.19. 某学校为了丰富学生课余生活,开展了“第二课堂”活动,推出了以下四种选修课程: .绘画; .唱歌; .跳舞; .演讲; .书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
请结合统计图中的信息解决下列问题:
(1)、这次抽查的学生人数是多少人?(2)、将条形统计图补充完整.(3)、求扇形统计图中课程 所对应扇形的圆心角的度数.(4)、如果该校共有1200名学生,请你估计该校选择课程 的学生约有多少人.20. 如图,小华和同伴在游玩期间,发现在某地小山坡的点 处有颗梅花树,他想利用平面镜测量的方式计算一下梅花树到山脚下的距离,即 的长度,小华站在点 的位置,让同伴移动平面镜至点 处,此时小华在平面镜内可以看到点 ,且 米, 米, ,已知小华的身高 为 米,请你利用以上的数据求出 的长度.(结果保留根号) 21. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段 表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线 表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题.
21. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段 表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线 表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题. (1)、轿车到达乙地时,求货车与甲地的距离.(2)、求线段 对应的函数表达式.(3)、在轿车行进过程中,轿车行驶多少时间,两车相距15千米.22. 小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至3层的任意一层出电梯,并设甲在 层出电梯,乙在b层出电梯.(1)、请你用画树状图或列表法求出甲、乙二人在同一层楼出电梯的概率.(2)、小亮和小芳打赌说:“若甲、乙在同一层或相邻楼层出电梯,则小亮胜,否则小芳胜”.该游戏是否公平?并说明理由.
(1)、轿车到达乙地时,求货车与甲地的距离.(2)、求线段 对应的函数表达式.(3)、在轿车行进过程中,轿车行驶多少时间,两车相距15千米.22. 小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至3层的任意一层出电梯,并设甲在 层出电梯,乙在b层出电梯.(1)、请你用画树状图或列表法求出甲、乙二人在同一层楼出电梯的概率.(2)、小亮和小芳打赌说:“若甲、乙在同一层或相邻楼层出电梯,则小亮胜,否则小芳胜”.该游戏是否公平?并说明理由.3层
2层
1层
车库
23. 如图,直线AM与⊙O相切于点A,弦BC AM,连接BO并延长,交⊙O于点E,交AM于点F,连接CE并延长,交AM于点D.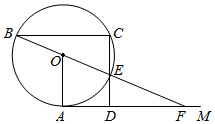 (1)、求证:CE OA;(2)、若⊙O的半径R=13,BC=24,求AF的长.24. 如图,抛物线y=﹣x2+bx+c过等腰Rt△OAB的A,B两点,点B在点A的右侧,直角顶点A(0,3).
(1)、求证:CE OA;(2)、若⊙O的半径R=13,BC=24,求AF的长.24. 如图,抛物线y=﹣x2+bx+c过等腰Rt△OAB的A,B两点,点B在点A的右侧,直角顶点A(0,3). (1)、求抛物线的表达式.(2)、P是AB上方抛物线上的一点,作PQ⊥AB交OB于点Q,连接AP,是否存在点P,使四边形APQO是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.25. 如图1,四边形ABCD是矩形,点P是对角线AC上的一个动点(不与A、C重合),过点P作PE⊥CD于点E,连接PB,已知AD=3,AB=4,设AP=m.
(1)、求抛物线的表达式.(2)、P是AB上方抛物线上的一点,作PQ⊥AB交OB于点Q,连接AP,是否存在点P,使四边形APQO是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.25. 如图1,四边形ABCD是矩形,点P是对角线AC上的一个动点(不与A、C重合),过点P作PE⊥CD于点E,连接PB,已知AD=3,AB=4,设AP=m.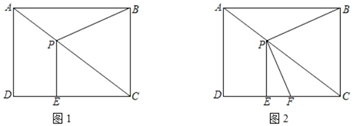 (1)、当m=1时,求PE的长;(2)、连接BE,试问点P在运动的过程中,能否使得△PAB≌△PEB?请说明理由;(3)、如图2,过点P作PF⊥PB交CD边于点F,设CF=n,试判断5m+4n的值是否发生变化,若不变,请求出它的值;若变化,请说明理由.
(1)、当m=1时,求PE的长;(2)、连接BE,试问点P在运动的过程中,能否使得△PAB≌△PEB?请说明理由;(3)、如图2,过点P作PF⊥PB交CD边于点F,设CF=n,试判断5m+4n的值是否发生变化,若不变,请求出它的值;若变化,请说明理由.