陕西省西安市长安区2021年数学中考一模试卷

试卷更新日期：2021-06-01 类型：中考模拟

进入出卷网下载

一、单选题

1. 比﹣5小3的数是（）

A、﹣2 B、2 C、﹣8 D、8

查看试题解析
2. 根据“头条”报道，2021年大年初一，长安区樊川公园当日客流量突破30万人，30万用科学记数法表示正确的是（）

A、0.3×10⁶ B、3×10⁶ C、3×10⁵ D、30×10⁴

查看试题解析
3. 下列计算正确的是（）

A、a²＋a³＝a⁵ B、（-2x²y）³＝-6x⁶y³ C、（a-b）（-a-b）＝a²-b² D、2x²（- $\frac{1}{3}$ xy）＝- $\frac{2}{3}$ x³y

查看试题解析
4. 如图，AB∥EF，∠B＝75°，∠FDC＝135°，则∠C的度数等于（）

A、30° B、35° C、45° D、60°

查看试题解析
5. 已知，正比例函数y＝kx的图象经过点（a，b），且 $\frac{a}{b}$ ＝2，则k的值等于（）

A、 $\frac{1}{2}$ B、2 C、﹣2 D、﹣ $\frac{1}{2}$

查看试题解析
6. 如图，在△ABC中，AD⊥BC于点D，且BD＝ $\frac{1}{2}$ CD，若△ABD的中线BF＝2，则AC的长为（）

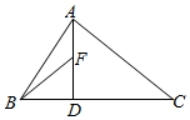A、5 B、4 C、3 D、2 $\sqrt{2}$

查看试题解析
7. 已知直线l₁过点（﹣1，0），直线l₂过点（0，2），且l₁和l₂关于直线x＝1对称，则直线l₁和l₂的交点坐标为（）

A、（1， $\frac{1}{3}$ ） B、（1， $\frac{4}{3}$ ） C、（1， $\frac{5}{3}$ ） D、（1， $\frac{7}{3}$ ）

查看试题解析
8. 如图，在正方形ABCD中，AB＝4 $\sqrt{5}$ .E，F分别为边AB，BC的中点，连接AF，DE，点N，M分别为AF，DE的中点，连接MN，则MN的长为（）

A、 $\sqrt{5}$ B、2 $\sqrt{5}$ C、 $\sqrt{10}$ D、2 $\sqrt{10}$

查看试题解析
9. 如图，在以AB为直径的半⊙O中， $\overset{⌢}{A C}$ ＝ $\overset{⌢}{B C}$ ，点D为 $\overset{⌢}{A C}$ 上一点，连接OC，BD交于点E，连接OD，若∠DEC＝65°，则∠DOC的度数等于（）

A、25° B、32.5° C、35° D、40°

查看试题解析
10. 已知，抛物线y＝ax²＋2ax在其对称轴的左侧y随x的增大而减小，关于x的方程ax²＋2ax＝m（m＞0）的一个根为﹣4，而关于x的方程ax²＋2ax＝n（0＜n＜m）有两个整数根，则这两个根的积是（）

A、0 B、﹣3 C、﹣6 D、﹣8

查看试题解析

二、填空题

11. 实数a在数轴上对应点的位置如图所示，若实数b满足﹣a＜b＜a，则b的值可以是（任填一个即可）.

查看试题解析
12. 如图所示的六边形花环是用六个全等的直角三角形拼成的，则 $∠ A B C$ 等于度．

查看试题解析
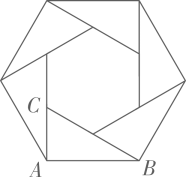13. 在平面直角坐标系中，直线y＝﹣x与双曲线y＝﹣ $\frac{k^{2} + 1}{x}$ 交于点A（x₁ ， y₁），B（x₂ ， y₂），则x₁﹣y₂的值为.

查看试题解析
14. 如图，在矩形ABCD中，AB＝2，BC＝4，边AD，BC上分别有E，F两点，若直线EF恰好平分矩形ABCD的面积，且与AD的夹角为60°时，则AE的长度为.

查看试题解析

三、解答题

15. 解不等式组： ${\begin{array}{l} 2 x \leq 6 - x ① \\ 3 x + 1 > 2 (x - 1) ② \end{array}$

查看试题解析
16. 分式化简：（x﹣1＋ $\frac{1}{x + 1}$ ）÷ $\frac{x^{2} + 2 x}{x + 1}$ .

查看试题解析
17. 如图，在△ABC中，AB＞AC，请你用无刻度的直尺和圆规在AB上找一点P，使得∠APC＝2∠B.（保留作图痕迹，不写作法）

查看试题解析
18. 如图，△ABD和△BCE都为等边三角形，连接AE、CD.求证：AE＝DC.

查看试题解析
19. 教育部颁发的《中小学教育惩戒规则（试行）》并从2021年3月1日起实行，某校随机抽取该校部分家长，按四个类别： $A$ 表示“非常支持”， $B$ 表示“支持”， $C$ 表示“不关心”， $D$ 表示“不支持”，调查他们对该规则态度的情况，将结果绘制成如下两幅不完整的统计图，
根据图中提供的信息，解决下列问题：

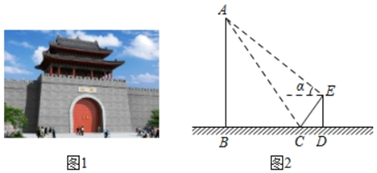
(1)、这次共抽取了名家长进行调查统计，扇形统计图中， $D$ 类所对应的扇形圆心角的大小是.

(2)、将条形统计图补充完整；

(3)、该学校共有2000名学生家长，估计该学校家长表示“支持”的（ $A$ 类， $B$ 类的和）人数大约有多少人？

查看试题解析
20. 如图1，是我区某村修建于清光绪年间的一座城门，某节假日随父亲回家的张菲同学想利用所学的数学知识测量此城门的高度.
如图2，她站在城门前方点D处，正好看到了城门顶端A点在地面小水潭（近似看成平面镜）里的倒影点C，此时他测得DC的长度为1米；接着她抬起头，目测城门顶端A点的仰角∠α的度数为39°，已知张菲同学的眼睛到地面的距离为1.5米，请你计算城门高度AB（结果精确到1米，sin39°≈0.63，cos39°≈0.78，tan39°≈0.81）.

查看试题解析
21. 某超市，二月底以60元/瓶的成本购进某种洗发露600瓶，并按照80元/瓶的单价销售，销售200瓶后正好遇上“三八妇女节”，商场决定当日以成本价销售，第二日恢复原价后，因库存量较少，超市又以60元/瓶的成本再次购进这种洗发露200瓶，当800瓶洗发露全部销售完后共获利12000元.请你根据下面销售利润y（元）与销售量x（瓶）之间的函数关系图象解答下列问题：

(1)、图中m＝， n＝；

(2)、求BC的解析式；

(3)、利用（2）中结论，计算当销售700瓶时超市获得的利润.

查看试题解析
22. 在初中毕业理化生实验复习备考中，化学田老师为本班学生准备了下面5个实验项目：A粗盐中难溶性杂质的去除；B.二氧化碳的实验室制取、验满及检验；C镁、锌、铁、铜主要化学性质的探究；D.配置50g质量分数为6%的氯化钠溶液；E.探究物质燃烧的条件.并准备了如图的五等分转盘，规定每名学生可转动一次转盘，并完成转盘停止后指针所指向的实验项目（若指针停在等分线上，则重新转动转盘）.
根据数学知识回答下列问题：

(1)、小明同学转动一次转盘，正好选中自己熟悉的“A”实验的概率是多少？

(2)、请你求出小明和小红两名同学各转动一次转盘，都没有选中“E”实验的概率（用树状图或列表法求解）.

查看试题解析
23. 如图，AB为⊙O的直径，C为BA延长线上一点，CD与⊙O相切于点D.OF⊥AD于点E，交CD于点F.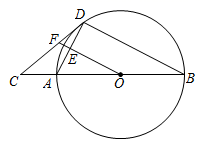

(1)、求证：∠ADC＝∠AOF；

(2)、若sinC＝ $\frac{3}{5}$ ，BD＝10，求EF的长.

查看试题解析
24. 如图，在平面直角坐标系中，点A的坐标为（﹣1，0），点B，点C分别为x轴，y轴正半轴上一点，其满足OC＝OB＝2OA.

(1)、求过A，B，C三点的抛物线的表达式；

(2)、连接CA，CB，若点P是x轴下方抛物线上的一点，连接PC，PB，当S_△PCB＝ $\frac{4}{3}$ S_△ACB时，求点P的坐标.

查看试题解析
25.

(1)、如图1，点A和点B是直线 $l_{1}$ 上两点，点C和点D是直线 $l_{2}$ 上两点，且 $l_{1} // l_{2}$ ，BC⊥AB，若AB＝2，BC＝3，则△ABD的面积为；

(2)、如图2，在边长为4的菱形ABCD中，∠A＝60°，M是边AD的中点，N是边AB上一动点，将△AMN沿直线MN翻折得到△PMN，求点P到直线BC的最小距离；

(3)、如图3，在矩形ABCD中，AD＝6，AB＝8，E，F分别为边CB，CD上的动点，且EF＝4，点O为EF的中点，连接BO并延长交CD于点M，过点O作ON∥DC交DB于点N，连接MN，则△BMN面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由.

查看试题解析