陕西省宝鸡市高新区2021年数学中考一模试卷
试卷更新日期:2021-06-01 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 已知∠A=75°,则∠A的补角等于( )A、125° B、105° C、15° D、95°3. 为了让市民出行更加方便,某市政府大力发展公共交通, 年该市公共交通客运量约为 人次,将 用科学记数法表示应为( )A、 B、 C、 D、4. 若正比例函数 的图象经过点 ,则 的值为( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,在 中, , , 平分 交 于点 , 的垂直平分线 交 于点 ,交 于点 ,若 ,则 的长为( )
 A、 B、 C、 D、7. 在平面直角坐标系中,将函数 的图象向左平移 个单位长度,则平移后的图象与 轴的交点坐标为( )A、 B、 C、 D、8. 如图,在矩形 中, , ,对角线 , 相交于点 ,过点 作 交 于点 ,则 的长为( )
A、 B、 C、 D、7. 在平面直角坐标系中,将函数 的图象向左平移 个单位长度,则平移后的图象与 轴的交点坐标为( )A、 B、 C、 D、8. 如图,在矩形 中, , ,对角线 , 相交于点 ,过点 作 交 于点 ,则 的长为( ) A、 B、 C、 D、9. 如图, 为 的直径, 为 的弦,若 ,则 的度数为( )
A、 B、 C、 D、9. 如图, 为 的直径, 为 的弦,若 ,则 的度数为( )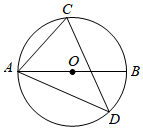 A、 B、 C、 D、10. 在平面直角坐标系中,有两条抛物线关于原点中心对称,且它们的顶点相距 个单位长度,若其中一条抛物线的函数表达式为 ,则 的值为( )A、 或 B、 或 C、 或 D、 或
A、 B、 C、 D、10. 在平面直角坐标系中,有两条抛物线关于原点中心对称,且它们的顶点相距 个单位长度,若其中一条抛物线的函数表达式为 ,则 的值为( )A、 或 B、 或 C、 或 D、 或二、填空题
-
11. 如图,直线 与 轴交于点 ,与反比例函数 的图象交于点 ,过点 作 轴于点 ,若 ,则反比例函数的表达式为.
 12. 如图,在矩形 中, , ,点 是矩形 内一动点,且 ,则 的最小值为.
12. 如图,在矩形 中, , ,点 是矩形 内一动点,且 ,则 的最小值为.
三、解答题
-
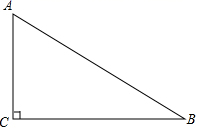
13. 计算: .14. 解分式方程: .15. 如图,在 中, ,用尺规在 上求作一点 ,使 到边 , 的距离相等(不写作法,保留作图痕迹).
 16. 如图,四边形 是平行四边形, , 是对角线 上的两点,且 .求证: .
16. 如图,四边形 是平行四边形, , 是对角线 上的两点,且 .求证: . 17. 为响应市上的“创卫”号召,某校倡议学生利用双休日在各自社区参加义务劳动,为了了解同学们的劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了如图所示的两幅不完整的统计图.
17. 为响应市上的“创卫”号召,某校倡议学生利用双休日在各自社区参加义务劳动,为了了解同学们的劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了如图所示的两幅不完整的统计图.学生双休日劳动时间条形统计图

学生双休日劳动时间扇形统计图

请根据图中信息解答下列问题:
(1)、将条形统计图补充完整;(2)、扇形统计图中“ 小时”部分圆心角的度数为 ;(3)、求所有被调查的同学劳动时间的中位数和平均数.18. 如图,新华中学教学楼 与实验楼 的水平间距 为 米,在实验楼顶部 点分别测得教学楼顶部 点的仰角为 ,底部 点的俯角为 ,求教学楼 的高度. 19. 某工厂每天生产 , 两种款式的布制环保购物袋共 个,已知 种购物袋成本为 元/个,售价为 元/个; 种购物袋成本为 元/个,售价为 元/个.设该工厂每天生产 种购物袋 个,每天共需成本 元,共获利 元.(1)、求 与 之间的函数表达式;(2)、求 与 之间的函数表达式;(3)、如果该工厂每天最多投入成本 元,那么每天最多获利多少元?20. 一个不透明的袋子中装有标号分别为 , , , 的四个小球,这些小球除标号数字外都相同.(1)、将袋子中的小球摇匀,然后从袋子中随机摸出一个小球,求摸到标号数字为偶数的小球的概率;(2)、小明和小华用这四个小球玩摸球游戏,规则是:将袋子中的小球摇匀,小明从袋子中随机摸出一个小球,记下标号数字后放回袋子里,然后再将袋子中的小球摇匀,小华此时从袋子中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字都是奇数,则小明获胜;若两次摸到小球的标号数字都是偶数,则小华获胜;否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止,请用列表法或画树状图的方法说明这个游戏规则对双方是否公平.21. 如图, 内接于 , 为 的直径, ,过点 作 的切线与 的延长线交于点 .
19. 某工厂每天生产 , 两种款式的布制环保购物袋共 个,已知 种购物袋成本为 元/个,售价为 元/个; 种购物袋成本为 元/个,售价为 元/个.设该工厂每天生产 种购物袋 个,每天共需成本 元,共获利 元.(1)、求 与 之间的函数表达式;(2)、求 与 之间的函数表达式;(3)、如果该工厂每天最多投入成本 元,那么每天最多获利多少元?20. 一个不透明的袋子中装有标号分别为 , , , 的四个小球,这些小球除标号数字外都相同.(1)、将袋子中的小球摇匀,然后从袋子中随机摸出一个小球,求摸到标号数字为偶数的小球的概率;(2)、小明和小华用这四个小球玩摸球游戏,规则是:将袋子中的小球摇匀,小明从袋子中随机摸出一个小球,记下标号数字后放回袋子里,然后再将袋子中的小球摇匀,小华此时从袋子中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字都是奇数,则小明获胜;若两次摸到小球的标号数字都是偶数,则小华获胜;否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止,请用列表法或画树状图的方法说明这个游戏规则对双方是否公平.21. 如图, 内接于 , 为 的直径, ,过点 作 的切线与 的延长线交于点 . (1)、求证: 为等边三角形;(2)、若 ,求 的长.22. 如图,抛物线 与 轴交于点 ,与 轴交于 , 两点,点 在点 的左侧,点 的坐标为 , .
(1)、求证: 为等边三角形;(2)、若 ,求 的长.22. 如图,抛物线 与 轴交于点 ,与 轴交于 , 两点,点 在点 的左侧,点 的坐标为 , . (1)、求抛物线的函数表达式;(2)、若点 在 轴上,点 在抛物线上,是否存在以 , , , 为顶点且以 为一边的平行四边形?若存在,求出点 的坐标;若不存在,请说明理由.23.(1)、(1)问题发现
(1)、求抛物线的函数表达式;(2)、若点 在 轴上,点 在抛物线上,是否存在以 , , , 为顶点且以 为一边的平行四边形?若存在,求出点 的坐标;若不存在,请说明理由.23.(1)、(1)问题发现如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE.

填空:
①∠AEB的度数为;
②线段AD、BE之间的数量关系为 .
(2)、拓展研究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
(3)、解决问题如图3,在正方形ABCD中,CD=2 ,若点P满足PD=2,且∠BPD=90°,请直接写出点A到BP的距离.