宁夏吴忠市盐池县(五校)2021年数学中考一模试卷
试卷更新日期:2021-06-01 类型:中考模拟
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 据科学检测,新冠病毒实际直径约为0.000011厘米,其中数据0.000011用科学记数法可以表示为( )A、 B、 C、 D、3. 下面左边第一个图是某一物体的三视图,则三视图对应的物体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 某县10名学生参加汉字听写大赛,他们得分情况如下表:
4. 某县10名学生参加汉字听写大赛,他们得分情况如下表:人数
分数
那么这10名学生所得分数的中位数和众数分别是( )
A、 和 B、 和 C、 和 D、 和5. 如图,在▱ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )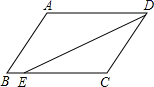 A、2cm B、4cm C、6cm D、8cm6. 如图,已知直线 ,含 角的三角板的直角顶点C在 上, 角的顶点A在 上,如果边 与 的交点D是 的中点,那么 的度数为( )
A、2cm B、4cm C、6cm D、8cm6. 如图,已知直线 ,含 角的三角板的直角顶点C在 上, 角的顶点A在 上,如果边 与 的交点D是 的中点,那么 的度数为( ) A、 B、 C、 D、7. 一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象可能是( )A、
A、 B、 C、 D、7. 一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 8. 如图1,一个扇形纸片的圆心角为90°,半径为4.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为( )
8. 如图1,一个扇形纸片的圆心角为90°,半径为4.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为( )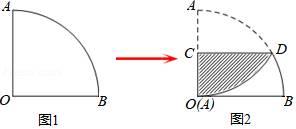 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
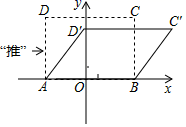
9. 分解因式: .10. 计算: =.11. 关于x的一元二次方程(k-2)x²-4x-3=0有两个不相等的实数根,则k的取值范围是.12. 在一个盒子中有红球,黑球,黄球共20个,每个球除颜色外都相同,从中任意摸出一球,得到红球的概率为 ,得到黑球的概率为 ,则这20个球中黄球有个.13. 如图,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,AO=2,BO=3,BC=4.将正方形沿箭头方向推,使点D落在y轴正半轴上点D’处,则点C的对应点C’的坐标为.
 14. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为m.
14. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为m. 15. 公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示.它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是40, ,则小正方形的面积是.
15. 公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示.它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是40, ,则小正方形的面积是. 16. 已知等边三角形 .如图,
16. 已知等边三角形 .如图,
( 1 )分别以点A,B为圆心,大于 的长为半径作弧,两弧相交于M,N两点;
( 2 )作直线 交 于点D;
( 3 )分别以点A,C为圆心,大于 的长为半径作弧,两弧相交于H,L两点;
( 4 )作直线 交 于点E;
( 5 )直线 与直线 相交于点O;
( 6 )连接 , , .
根据以上作图过程及所作图形,下列结论:
① ;② ;③ ;④ ,正确的是.
三、解答题
-
17. 如图,在平面直角坐标系中,给出了格点 (顶点均在正方形网格的格点上),已知点 的坐标为 .
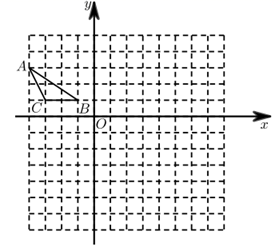 (1)、画出 关于 轴对称的 .(2)、以点 为位似中心,在给定的网格中画 ,使 与 位似,且位似比为 .18. 解分式方程:19. 解不等式组20. 如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.
(1)、画出 关于 轴对称的 .(2)、以点 为位似中心,在给定的网格中画 ,使 与 位似,且位似比为 .18. 解分式方程:19. 解不等式组20. 如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E. (1)、求证:BD=BE;(2)、若∠DBC=30°,BO=4,求四边形ABED的面积.21. 疫情期间,某药店计划从一口罩厂采购同一品牌的甲型口罩和乙型口罩,已知购买1盒甲型口罩和2盒乙型口罩,需花费21元,购买10盒甲型口罩和4盒乙型口罩,需花费82元.(1)、求采购该品牌一盒甲型口罩、一盒乙型口罩各需要多少元?(2)、经商谈,口罩厂给予该药店采购一盒该品牌乙型口罩即赠送一盒该品牌甲型口罩的优惠,如果药店需要甲型口罩的盒数是乙型口罩盒数的2倍还多8盒,且该药店采购甲型口罩和乙型口罩的总费用不超过1340元,那么该药店最多可购买多少盒该品牌乙型口罩?22. 中央电视台的“中国诗词大赛”节目文化品位高,内容丰富.某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:
(1)、求证:BD=BE;(2)、若∠DBC=30°,BO=4,求四边形ABED的面积.21. 疫情期间,某药店计划从一口罩厂采购同一品牌的甲型口罩和乙型口罩,已知购买1盒甲型口罩和2盒乙型口罩,需花费21元,购买10盒甲型口罩和4盒乙型口罩,需花费82元.(1)、求采购该品牌一盒甲型口罩、一盒乙型口罩各需要多少元?(2)、经商谈,口罩厂给予该药店采购一盒该品牌乙型口罩即赠送一盒该品牌甲型口罩的优惠,如果药店需要甲型口罩的盒数是乙型口罩盒数的2倍还多8盒,且该药店采购甲型口罩和乙型口罩的总费用不超过1340元,那么该药店最多可购买多少盒该品牌乙型口罩?22. 中央电视台的“中国诗词大赛”节目文化品位高,内容丰富.某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题: (1)、扇形统计图中“优秀”所对应扇形的圆心角为__▲_度,并将条形统计图补充完整.(2)、此次比赛有四名同学获得满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.23. 如图,AB是⊙O的直径,点F,C是⊙O上两点,且 = = ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)、扇形统计图中“优秀”所对应扇形的圆心角为__▲_度,并将条形统计图补充完整.(2)、此次比赛有四名同学获得满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.23. 如图,AB是⊙O的直径,点F,C是⊙O上两点,且 = = ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D. (1)、求证:CD是⊙O的切线;(2)、若CD=2 ,求⊙O的半径.24. “五•一”假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票.经调查发现,在车站开始检票时,有640人排队检票.检票开始后,仍有旅客继续前来排队检票进站.设旅客按固定的速度增加,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人.已知检票的前a分钟只开放了两个检票口.某一天候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.
(1)、求证:CD是⊙O的切线;(2)、若CD=2 ,求⊙O的半径.24. “五•一”假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票.经调查发现,在车站开始检票时,有640人排队检票.检票开始后,仍有旅客继续前来排队检票进站.设旅客按固定的速度增加,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人.已知检票的前a分钟只开放了两个检票口.某一天候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.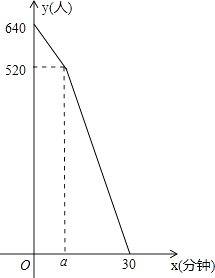 (1)、求a的值.(2)、求检票到第20分钟时,候车室排队等候检票的旅客人数.(3)、若要在开始检票后15分钟内让所有排队的旅客都能检票进站,以便后来到站的旅客随到随检,问检票一开始至少需要同时开放几个检票口?25. A、B两地果园分别有橘子40吨和60吨,C、D两地分别需要橘子30吨和70吨;已知从A、B到C、D的运价如表:
(1)、求a的值.(2)、求检票到第20分钟时,候车室排队等候检票的旅客人数.(3)、若要在开始检票后15分钟内让所有排队的旅客都能检票进站,以便后来到站的旅客随到随检,问检票一开始至少需要同时开放几个检票口?25. A、B两地果园分别有橘子40吨和60吨,C、D两地分别需要橘子30吨和70吨;已知从A、B到C、D的运价如表:到C地
到D地
A果园
每吨15元
每吨12元
B果园
每吨10元
每吨9元
(1)、若从A果园运到C地的橘子为x吨,则从A果园运到D地的橘子为吨,从A果园将橘子运往D地的运输费用为元;(2)、设总运费为y元,请你求出y关于 的函数关系式;(3)、求总运输费用的最大值和最小值;(4)、若这批橘子在C地和D地进行再加工,经测算,全部橘子加工完毕后总成本为w元,且w=-(x-25)2+4360,则当x= 时,w有最 值(填“大”或“小”).这个值是 .26. 如图,已知等边 的边长为 ,点 、 分别在 、 边上, . (1)、把 沿 折叠,使得点 的对应点是点 落在 边上(如图1).求折痕 的长度;(2)、如图2,若点 在 上运动,且始终保持
(1)、把 沿 折叠,使得点 的对应点是点 落在 边上(如图1).求折痕 的长度;(2)、如图2,若点 在 上运动,且始终保持①请判断 和 是否相似?并说明理由;
②当点 在何位置时线段 长度最大,并求出线段 长度的最大值.