江苏省盐城市亭湖区2021年数学中考一模试卷

试卷更新日期：2021-06-01 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 2$ 的相反数是（）

A、 $- 2$ B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列各式计算正确的是（）

A、x+x²=x³ B、 ${(x^{2})}^{3} = x^{5}$ C、 $x^{6} \div x^{2} = x^{3}$ D、 $x \cdot x^{2} = x^{3}$

查看试题解析
4. 在九年级一次数学单元测验中，某班一个学习小组6人的成绩（单位：分）分别为：85、87、98、70、84、87.则这组数据的中位数和众数分别是（）

A、86和89 B、86和87 C、85和86 D、87和87

查看试题解析
5.
如图是由4个完全相同的小正方体组成的立体图形，则它的俯视图是（　　）

A、 B、 C、 D、

查看试题解析
6. 若x、y满足方程组 ${\begin{matrix} 4 x - y = 8 \\ x + 2 y = 2 \end{matrix}$ ，则x﹣y的值为（）

A、﹣2 B、﹣1 C、1 D、2

查看试题解析
7. 如图，AB是 $⊙ O$ 的直径，点C，D在 $⊙ O$ 上， $∠ D = 20 °$ ，则 $∠ 1$ 的大小是（）

A、 $160 °$ B、 $140 °$ C、 $150 °$ D、 $40 °$

查看试题解析
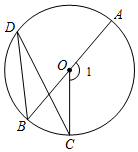8. 如图，已知△ABC中，AB=10 ，AC=8 ，BC = 6 ，DE是AC的垂直平分线，DE交AB于点D ，交AC于点E ，连接CD ，则CD的长度为（）

A、3 B、4 C、4.8 D、5

查看试题解析

二、填空题

9. 函数 $y = \sqrt{x - 1}$ 中自变量x的取值范围是.

查看试题解析
10. 清明时节，正是赏楼进行时.今年清明小长假期间，盐城大洋湾景区共迎接游客近300000人次.把300000用科学记数法表示为.

查看试题解析
11. 如图，在 $Rt △ A B C$ 中， $∠ B = 90 °$ ，点O在边AB上，以点O为圆心，OA为半径的圆经过点C，过点C作直线MN，使 $∠ B C M = 2 ∠ A$ .若 $O A = 4$ ， $∠ B C M = 60 °$ ，求图中阴影部分的面积.

查看试题解析
12. 如果 $2 a + b = 1$ ，那么 $4 a + 2 b - 1$ 的值等于.

查看试题解析
13. 如果点P（x，y）的坐标满足x+y=xy，那么称点P为“和谐点”，若某个“和谐点“P到x轴的距离为2，则P点的坐标为.

查看试题解析
14. 如图，在菱形ABCD中，点E是BC的中点，以C为圆心，CE为半径作弧，交CD于点F，连接AE、AF.若AB=6，∠B=60°，则阴影部分的面积为.

查看试题解析
15. 如图，抛物线 $y = a x^{2} + c$ 与直线 $y = m x + n$ 交于A(-1，P)，B(3，q)两点，则不等式 $a x^{2} + m x + c > n$ 的解集是．

查看试题解析

三、解答题

16. 计算： ${(\frac{1}{2})}^{- 1} - \sqrt{16} + 4 \cos 60 °$ .

查看试题解析
17. 解不等式组： ${\begin{array}{l} 2 (x + 1) - 3 < 5 \\ x - 2 \geq \frac{x - 4}{3} \end{array}$ .

查看试题解析
18. 先化简，再求值： $(\frac{1}{x + 1} + 1) \div \frac{x^{2} - 4}{x + 1}$ ，其中 $x = 5$

查看试题解析
19. 在一个不透明的盒子中装有三张卡片，分别标有数字为1，2，7，这些卡片除数字不同外其余均相同.洗匀后，小强从盒子中随机抽取一张卡片记下数字后放回，洗匀后再随机抽取一张卡片.用画树状图或列表的方法，求两次抽取的卡片上数字之和为偶数的概率.

查看试题解析
20. 随着科技的进步和网络资源的丰富，在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论.为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查（每人只选一类），并根据调查结果绘制成如下两幅不完整的统计图.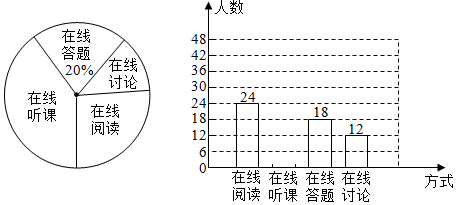

根据图中信息，解答下列问题：

(1)、求本次调查的学生总人数，并补全条形统计图；

(2)、求扇形统计图中“在线讨论”对应的扇形圆心角的度数；

(3)、该校共有学生2700人，请你估计该校对在线阅读最感兴趣的学生人数.

查看试题解析
21. 已知：如图，在 $△ A B C$ 中， $A B = A C ， D$ 为边 $B C$ 上一点，以 $A B ， B D$ 为邻边作平行四边形 $A B D E$ ，连接 $A D ， E C$ .

(1)、求证： $∠ 1 = ∠ 2$ ；

(2)、求证： $△ A D C ≌ △ E C D$ ；

(3)、当点 $D$ 在什么位置时，四边形 $A D C E$ 是矩形，请说明理由.

查看试题解析
22. 智能手机如果安装了一款测量软件“Smart Measure”后，就可以测量物高、宽度和面积等，如图，打开软件后将手机摄像头对准脚部按键，再对准头部按键，即可测量出人体的高度.测量者AB用其数学原理如图②所示，测量一棵大树CD，手机显示 $A C = 20 m$ ， $A D = 25 m$ ， $∠ C A D = 53 °$ ，求此时CD的高.（结果保留根号）（ $\sin 53 ° \approx \frac{4}{5}$ ， $\cos 53 ° \approx \frac{3}{5}$ ， $\tan 53 ° \approx \frac{4}{3}$ ）

查看试题解析
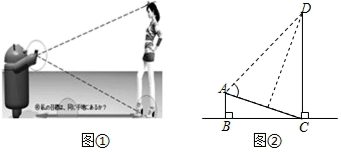23. 如图，AB是⊙O的直径，C是⊙O上的一点，连接AC ， BC ， D是AB上的一点，过点D作AB的垂线，与线段BC交于点E ，点F在线段DE的延长线上，且满足FC＝FE ．

(1)、求直线CF与⊙O的公共点个数；

(2)、当点E恰为BC中点时，若⊙O的半径为5，tanA＝ $\frac{4}{3}$ ，求线段CF的长．

查看试题解析
24. 如图，一次函数 $y = m x + 1$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象相交于A、B两点，点C在x轴负半轴上，点 $D (- 1 ， - 2)$ ，连接OA、OD、DC、AC，四边形 $O A C D$ 为菱形.

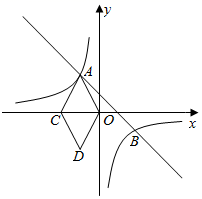(1)、求一次函数与反比例函数的解析式；

(2)、根据图象，直接写出反比例函数的值小于2时，x的取值范围；

(3)、设点P是直线AB上一动点，且 $S_{△ O A P} = \frac{1}{2} S_{菱形 O A C D}$ ，求点P的坐标.

查看试题解析
25. 如图，已知 $△ A B C$ 和 $△ A D E$ 均为等腰三角形， $A C = B C$ ， $D E = A E$ ，将这两个三角形放置在一起.

(1)、问题发现：
如图①，当 $∠ A C B = ∠ A E D = 60 °$ 时，点B、D、E在同一直线上，连接CE，则线段BD、CE之间的数量关系是， $∠ C E B =$ $°$ ；

(2)、拓展探究：
如图②，当 $∠ A C B = ∠ A E D = α$ 时，点B、D、E不在同一直线上，连接CE，求出线段BD、CE之间的数量关系及BD、CE所在直线相交所成的锐角的大小（都用含 $α$ 的式子表示），并说明理由：

(3)、解决问题：
如图③， $∠ A C B = ∠ A E D = 90 °$ ， $A C = \sqrt{10}$ ， $A E = \sqrt{2}$ ，连接CE、BD，在 $△ A E D$ 绕点A旋转的过程中，当CE所在的直线垂直于AD时，请你直接写出BD的长.

查看试题解析
26. 如图，已知抛物线 $y = a x^{2} + b x - 3$ 与x轴交于 $A (- 2 ， 0)$ 、 $B (6 ， 0)$ 两点，与y轴交于C点，设抛物线的顶点为D.过点D作 $D E ⊥ x$ 轴，垂足为E.P为线段DE上一动点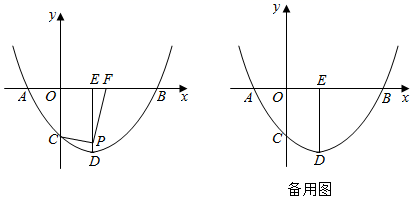， $F (m ， 0)$ 为x轴上一点，且 $P C ⊥ P F$ .

(1)、求抛物线的解析式：

(2)、①当点P与点D重合时，求m的值；
②在①的条件下，将 $△ C O F$ 绕原点按逆时针方向旋转 $90 °$ 并平移，得到 $△ C_{1} O_{1} F_{1}$ ，点C，O，F的对应点分别是点 $C_{1}$ ， $O_{1}$ ， $F_{1}$ ，若 $△ C O F$ 的两个顶点恰好落在抛物线上，直接写出点 $F_{1}$ 的坐标；

(3)、当点P在线段DE上运动时，求m的变化范围.

查看试题解析