江苏省盐城市滨海县2021年数学中考一模试卷
试卷更新日期:2021-06-01 类型:中考模拟
一、单选题
-
1. 有理数2021的相反数为( )A、2021 B、-2021 C、 D、2. 若式子 有意义,则x的值可以为( )A、2 B、﹣2 C、﹣1 D、03. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,菊花1角硬币为外圆内正九边形的边缘异形币,则该正九边形的一个内角的大小为( )
4. 如图,菊花1角硬币为外圆内正九边形的边缘异形币,则该正九边形的一个内角的大小为( ) A、 B、 C、 D、5. 如图所示, ,三角板 如图放置,其中 ,若 ,则 的度数是( )
A、 B、 C、 D、5. 如图所示, ,三角板 如图放置,其中 ,若 ,则 的度数是( )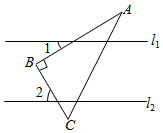 A、 B、 C、 D、6. 一个不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是必然事件的是( )A、3个球都是黑球 B、3个球都是白球 C、3个球中有黑球 D、3个球中有白球7. 如图,下图经过折叠不能围成一个正方体是( )A、
A、 B、 C、 D、6. 一个不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是必然事件的是( )A、3个球都是黑球 B、3个球都是白球 C、3个球中有黑球 D、3个球中有白球7. 如图,下图经过折叠不能围成一个正方体是( )A、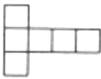 B、
B、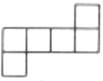 C、
C、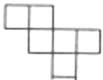 D、
D、 8. 如图,矩形ABCD的对角线AC、BD相交于点O,∠ABO=60°,若矩形的对角线长为6.则线段AD的长是( )
8. 如图,矩形ABCD的对角线AC、BD相交于点O,∠ABO=60°,若矩形的对角线长为6.则线段AD的长是( ) A、3 B、4 C、2 D、3
A、3 B、4 C、2 D、3二、填空题
-
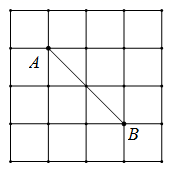
9. 若|﹣1﹣2|=.10. 已知x+y=6,xy=7,则x2y+xy2的值是.11. 如图,点 、点 均在边长为 的正方形网格的格点上,则线段 的长度3.(填“>”, “=”或“<”)
 12. 目前我国芯片已可采用14纳米工艺.已知14纳米为0.000000014米,数据0.000000014用科学记数法表示为.13. 如图,已知直线y=mx与双曲线y= 一个交点坐标为(3,4),则它们的另一个交点坐标是.
12. 目前我国芯片已可采用14纳米工艺.已知14纳米为0.000000014米,数据0.000000014用科学记数法表示为.13. 如图,已知直线y=mx与双曲线y= 一个交点坐标为(3,4),则它们的另一个交点坐标是. 14. 如图,两条直线l1和l2的关系式分别为y1=k1x+b1 , y2=k2x+b2 , 两直线的交点坐标为(2,1),当y1>y2时,x的取值范围为.
14. 如图,两条直线l1和l2的关系式分别为y1=k1x+b1 , y2=k2x+b2 , 两直线的交点坐标为(2,1),当y1>y2时,x的取值范围为.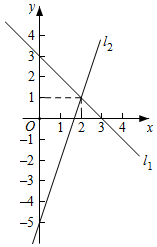 15. 如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠A=30°,则sinE的值为.
15. 如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠A=30°,则sinE的值为. 16. 如图,在平行四边形ABCD中,∠A = 45°,AB = 6,AD = 2 ,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
16. 如图,在平行四边形ABCD中,∠A = 45°,AB = 6,AD = 2 ,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
三、解答题
-
17. 计算: .18. 解方程:19. 解不等式组: .20. 红岭中学最近要举办艺术节,节目分别有:A舞蹈、B戏剧、C唱歌、D漫画与书法.下面随机抽取部分同学调查最喜爱哪项节目,得到如图两幅不完整的统计图.
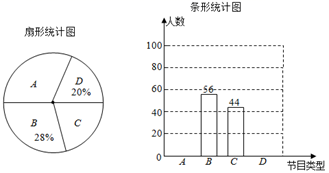
请你根据统计图提供的信息,解答下列问题:
(1)、本次一共调查了名同学.(2)、请补全条形统计图,在扇形统计图中A类型节目所对应的圆心角为 度.(3)、在本次调查访问中,小明和小亮从“舞蹈”、“戏剧”、“唱歌”,选出一种自己最喜欢的节目.请用树状图或列表法求出两人恰好选择同一种节目的概率.21. 4月23日是世界读书日,全称为世界图书与版权日,又称“世界图书日”,设立的目的是推动更多的人去阅读和写作,希望所有人都能尊重和感谢为人类文明做出过巨大贡献的文学、文化、科学、思想大师们,保护知识产权.习近平说:“我爱好挺多,最大的爱好是读书,读书已成为我的一种生活方式,读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”学校某兴趣小组为了了解学生课外阅读的情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:(收集数据)从学校随机抽取 名学生,进行了每周用于课外阅读时间的调查,数据如下(单位: ):
(整理数据)按如下分段整理样本数据:
课外阅读时间
人数
(分析数据)对样本数据进行分析得到如下分析表:
平均数
中位数
众数
(得出结论)
(1)、补全分析表中的数据: , ;(2)、如果该校现有学生 人,请估计每周阅读时间超过 的学生有多少名?(3)、假设平均阅读一本课外书的时间为 分钟,请你选择一种统计量估计该校学生每人一年(按 周计算)平均阅读多少本课外书?22. 以下各图均是由边长为1的小正方形组成的网格,图中的点A、B、C、D均在格点上. (1)、在图①中,PC:PB= .(2)、利用网格和无刻度的直尺作图,保留痕迹,不写作法.
(1)、在图①中,PC:PB= .(2)、利用网格和无刻度的直尺作图,保留痕迹,不写作法.①如图②,在AB上找一点P , 使AP=3.
②如图③,在BD上找一点P , 使△APB∽△CPD .
23. 如图,在平行四边形 中, ,点 是 的中点,连接 并延长,交 的延长线于点 ,连接 .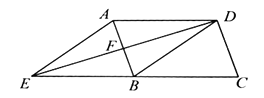 (1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的面积.24. 如图,在山顶上有一座电视塔,为测量山高,在地面上引一条基线EDC,测得 =45°,CD=60m, =30°.已知电视塔高AB=150m,求山高BE的值.(参考数据: 1.414, 1.732,精确到1m).
(1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的面积.24. 如图,在山顶上有一座电视塔,为测量山高,在地面上引一条基线EDC,测得 =45°,CD=60m, =30°.已知电视塔高AB=150m,求山高BE的值.(参考数据: 1.414, 1.732,精确到1m). 25. 如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
25. 如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求: (1)、PA的长;
(1)、PA的长;
(2)、∠COD的度数.26. 某种食品的销售价格 与销售月份 之间的关系如图1所示,成本 与销售月份 之间的关系如图2所示(图1的图象是线段,图2的图象是部分抛物线). (1)、已知6月份这种食品的成本最低,求当月出售这种食品每千克的利润(利润 售价 成本)是多少?(2)、求出售这种食品的每千克利润p与销售月份 之间的函数关系式;(3)、哪个月出售这种食品,每千克的利润最大?最大利润是多少?简单说明理由.27. 如图,在平面直角坐标系中,直线y=kx﹣4与反比例函数y= (x>0)的图象交于点A,与y轴交于点C.点B在x轴上,∠ABO=90°,AB=BO.
(1)、已知6月份这种食品的成本最低,求当月出售这种食品每千克的利润(利润 售价 成本)是多少?(2)、求出售这种食品的每千克利润p与销售月份 之间的函数关系式;(3)、哪个月出售这种食品,每千克的利润最大?最大利润是多少?简单说明理由.27. 如图,在平面直角坐标系中,直线y=kx﹣4与反比例函数y= (x>0)的图象交于点A,与y轴交于点C.点B在x轴上,∠ABO=90°,AB=BO.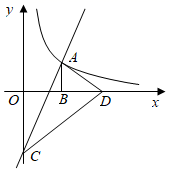 (1)、求k的值;(2)、点D(m,0)在x轴正半轴上,连接AD,CD, ACD是以AC为斜边的直角三角形.请用两种不同的方法求m的值.(3)、在(2)的条件下,点E在反比例函数的图象上(不与A重合),若 ,请求出点E的坐标.(4)、若P为直线y=kx﹣4上的动点,Q为反比例函数y= (x>0)的图象上的动点,且以点P、Q、O、C为顶点的四边形是平行四边形,请直接写出点P的坐标.
(1)、求k的值;(2)、点D(m,0)在x轴正半轴上,连接AD,CD, ACD是以AC为斜边的直角三角形.请用两种不同的方法求m的值.(3)、在(2)的条件下,点E在反比例函数的图象上(不与A重合),若 ,请求出点E的坐标.(4)、若P为直线y=kx﹣4上的动点,Q为反比例函数y= (x>0)的图象上的动点,且以点P、Q、O、C为顶点的四边形是平行四边形,请直接写出点P的坐标.