江苏省无锡市锡山区2021年数学中考一模试卷
试卷更新日期:2021-06-01 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 函数y= 中自变量x的取值范围是( )A、x>2 B、x≥2 C、x≤2 D、x≠23. 下列运算中,正确的是( )A、 B、 C、 D、4. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 已知一组数据:21,23,25,25,26,这组数据的平均数和中位数分别是( )A、24,25 B、24,24 C、25,24 D、25,256. 已知 是方程 的一个解,那么 的值是( )A、-2 B、2 C、-4 D、47. 如图是由几个相同的小正方体搭成的一个几何体,它的俯视图是( )
5. 已知一组数据:21,23,25,25,26,这组数据的平均数和中位数分别是( )A、24,25 B、24,24 C、25,24 D、25,256. 已知 是方程 的一个解,那么 的值是( )A、-2 B、2 C、-4 D、47. 如图是由几个相同的小正方体搭成的一个几何体,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,平行于y轴的直线分别交 与 的图象(部分)于点A、B,点C是y轴上的动点,则 的面积为( )
8. 如图,平行于y轴的直线分别交 与 的图象(部分)于点A、B,点C是y轴上的动点,则 的面积为( ) A、 B、 C、 D、9. 如图,矩形 中, ,以 为圆心,3为半径作 , 为 上一动点,连接 ,以 为直角边作 ,使 , ,则点 与点 的最小距离为( )
A、 B、 C、 D、9. 如图,矩形 中, ,以 为圆心,3为半径作 , 为 上一动点,连接 ,以 为直角边作 ,使 , ,则点 与点 的最小距离为( )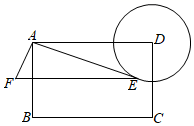 A、 B、 C、 D、10. 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 , 且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
A、 B、 C、 D、10. 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 , 且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是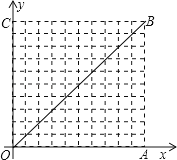 A、16 B、15 C、14 D、13
A、16 B、15 C、14 D、13二、填空题
-
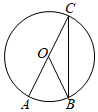
11. 因式分解: = .12. 人均 是衡量一个地区经济繁荣程度的重要指标,2020年无锡市的人均 约为187700元,其中数据187700用科学记数法表示为 .13. 圆锥的母线长为6cm,底面圆半径为4cm,则这个圆锥的侧面积为 cm2 .14. 请写出“两直线平行,同位角相等”的逆命题: .15. 如图,在 中, 为 直径, 为圆上一点,若 ,则 的度数为 .
 16. 如图,在边长为3的正六边形ABCDEF中,将四边形ADEF绕点A顺时针旋转到四边形 处,此时边 与对角线AC重叠,则图中阴影部分的面积是.
16. 如图,在边长为3的正六边形ABCDEF中,将四边形ADEF绕点A顺时针旋转到四边形 处,此时边 与对角线AC重叠,则图中阴影部分的面积是.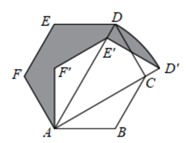 17. 如图,矩形 中, 为边 上一点,将 沿 折叠,使点 的对应点 恰好落在边 上,连接 交 于点 ,连接 .若 , ,则 .
17. 如图,矩形 中, 为边 上一点,将 沿 折叠,使点 的对应点 恰好落在边 上,连接 交 于点 ,连接 .若 , ,则 .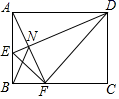 18. 如图, 在第一象限,其面积为16,点 从点 出发,沿 的边从 运动一周,在点 运动的同时,作点 关于原点 的对称点 ,再以 为边作等边三角形 ,点 在第二象限,点 随点 运动所形成的图形的面积为 .
18. 如图, 在第一象限,其面积为16,点 从点 出发,沿 的边从 运动一周,在点 运动的同时,作点 关于原点 的对称点 ,再以 为边作等边三角形 ,点 在第二象限,点 随点 运动所形成的图形的面积为 .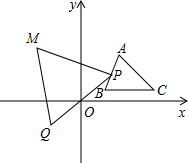
三、解答题
-
19. 如图①,将▱ABCD置于直角坐标系中,其中BC边在x轴上(B在C的左边),点D坐标为(0,4),直线MN: 沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被▱ABCD截得的线段长度为m,平移时间为t,m与t的函数图象如图②所示.
 (1)、填空:点C的坐标为;在平移过程中,该直线先经过B、D中的哪一点? ;(填“B”或“D”)(2)、点B的坐标为 , n= ,a=;(3)、在平移过程中,求该直线扫过▱ABCD的面积y与t的函数关系式.20.(1)、计算: .(2)、化简: .21.(1)、解方程: .(2)、解不等式组: .22. 如图,在▱ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.求证:∠BAE=∠CDF.
(1)、填空:点C的坐标为;在平移过程中,该直线先经过B、D中的哪一点? ;(填“B”或“D”)(2)、点B的坐标为 , n= ,a=;(3)、在平移过程中,求该直线扫过▱ABCD的面积y与t的函数关系式.20.(1)、计算: .(2)、化简: .21.(1)、解方程: .(2)、解不等式组: .22. 如图,在▱ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.求证:∠BAE=∠CDF.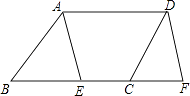 23. 随着延时服务的全面展开,某校组织了丰富多彩的社团活动,小红和小明分别打算从以下四个社团: 、3D制作打印, 、趣味数学, 、文学欣赏, 、乐高机器人中,选择一个社团参加.(1)、小红选择趣味数学的概率为 .(2)、用画树状图或列表的方法求小红和小明选择同一个社团的概率.24. 随着科技的进步和网络资源的丰富,在线阅读已成为很多人选择的阅读方式.为了解同学们在线阅读情况,某校园小记者随机调查了本校部分同学,并统计他们平均每天的在线阅读时间t(单位: ),然后利用所得数据绘制成如下不完整的统计图表.
23. 随着延时服务的全面展开,某校组织了丰富多彩的社团活动,小红和小明分别打算从以下四个社团: 、3D制作打印, 、趣味数学, 、文学欣赏, 、乐高机器人中,选择一个社团参加.(1)、小红选择趣味数学的概率为 .(2)、用画树状图或列表的方法求小红和小明选择同一个社团的概率.24. 随着科技的进步和网络资源的丰富,在线阅读已成为很多人选择的阅读方式.为了解同学们在线阅读情况,某校园小记者随机调查了本校部分同学,并统计他们平均每天的在线阅读时间t(单位: ),然后利用所得数据绘制成如下不完整的统计图表.在线阅读时间频数分布表
组别
在线阅读时间t
(人数)
A
4
B
8
C
a
D
16
E
2
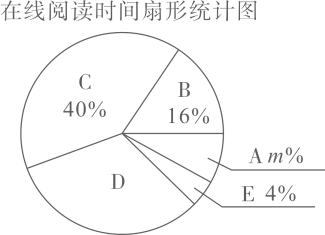
根据以上图表,解答下列问题:
(1)、这次被调查的同学共有人, , ;(2)、求扇形统计图中扇形D的圆心角的度数;(3)、若该校有950名学生,请估计全校有多少学生平均每天的在线阅读时间不少于 ?25. 如图,已知点 是 中 边上的一点,点 位于线段 上,利用直尺(无刻度)和圆规求作 ,使 过点 且与 相切.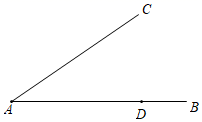 26. 如图, 为 的直径,四边形 内接于 ,对角线 , 交于点E, 的切线 交 的延长线于点F,切点为A,且 .
26. 如图, 为 的直径,四边形 内接于 ,对角线 , 交于点E, 的切线 交 的延长线于点F,切点为A,且 .
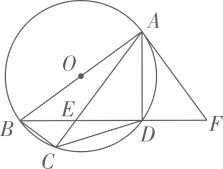 (1)、求证: ;(2)、若 ,求 的值.27. 2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数 (人)与时间 (分钟)的变化情况,数据如下表:(表中9-15表示 )
(1)、求证: ;(2)、若 ,求 的值.27. 2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数 (人)与时间 (分钟)的变化情况,数据如下表:(表中9-15表示 )时间 (分钟)
0
1
2
3
4
5
6
7
8
9
9~15
人数 (人)
0
170
320
450
560
650
720
770
800
810
810
(1)、根据这15分钟内考生进入考点的累计人数与时间的变化规律,利用初中所学函数知识求出y与x之间的函数关系式;(2)、如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?(3)、在(2)的条件下,如果要在12分钟内让全部考生完成体温检测,从一开始就应该至少增加几个检测点?28. 如图,抛物线y= x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(-3,0)和B.将抛物线y=
x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(-3,0)和B.将抛物线y=  x2+bx+c绕点B逆时针方向旋转90°,点M1 , A1为点M,A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.
x2+bx+c绕点B逆时针方向旋转90°,点M1 , A1为点M,A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.
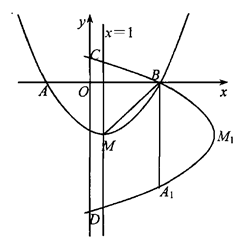 (1)、写出点B的坐标及求原抛物线的解析式:(2)、求证A,M,A1三点在同一直线上:(3)、设点P是旋转后抛物线上DM1之间的一动点,是否存在一点P,使四边形PM1MD的面积最大.如果存在,请求出点P的坐标及四边形PM1MD的面积;如果不存在,请说明理由.
(1)、写出点B的坐标及求原抛物线的解析式:(2)、求证A,M,A1三点在同一直线上:(3)、设点P是旋转后抛物线上DM1之间的一动点,是否存在一点P,使四边形PM1MD的面积最大.如果存在,请求出点P的坐标及四边形PM1MD的面积;如果不存在,请说明理由.