江苏省泰州市靖江市2021年数学中考一模试卷
试卷更新日期:2021-06-01 类型:中考模拟
一、单选题
-
1. ﹣2的绝对值是( )A、2 B、 C、 D、2. 我国是最早认识负数,并进行相关运算的国家在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算 的过程按照这种方法,图2表示的过程应是在计算( )

 A、 B、 C、 D、3. 下列图形中既是中心对称又是轴对称的是( )
A、 B、 C、 D、3. 下列图形中既是中心对称又是轴对称的是( ) A、可回收垃圾 B、其他垃圾 C、有害垃圾 D、厨余垃圾4. 下列各式中计算正确的是( )A、 B、 C、 D、5. 已知 、 是关于 的方程 的两根,下列结论中不一定正确的是( )A、 B、 C、 D、方程必有一正根6. 如图,AB为⊙O的直径,C为⊙O上一点,点D为半圆AB的中点,CD交AB于点E,若AC=8,BC=6,则BE的长为( )
A、可回收垃圾 B、其他垃圾 C、有害垃圾 D、厨余垃圾4. 下列各式中计算正确的是( )A、 B、 C、 D、5. 已知 、 是关于 的方程 的两根,下列结论中不一定正确的是( )A、 B、 C、 D、方程必有一正根6. 如图,AB为⊙O的直径,C为⊙O上一点,点D为半圆AB的中点,CD交AB于点E,若AC=8,BC=6,则BE的长为( ) A、4.25 B、 C、3 D、4.8
A、4.25 B、 C、3 D、4.8二、填空题
-
7. 若分式 的值为0,则x的值为.8. 点 到x轴的距离是 .9. 我国高铁通车总里程居世界第一,到2020年末高铁总里程达到37900千米,37900用科学记数法表示为.10. 正六边形的内角和为度.11. 若 ,则 的值为 .12. 四边形 中, ,顺次连接它的各边中点所得的四边形是.13. 如图,圆锥底面半径为 ,母线长为 ,侧面展开图是圆心角等于 的扇形,则该圆锥的底面半径 为 .
 14. 如图,在 中, , 是 中点, ,垂足为 ,若 ,则 .
14. 如图,在 中, , 是 中点, ,垂足为 ,若 ,则 . 15. 如图,直线 与x轴交于点B,与双曲线 (x>0)交于点A,过点B作x轴的垂线,与双曲线 交于点C.且AB=AC,则k的值为.
15. 如图,直线 与x轴交于点B,与双曲线 (x>0)交于点A,过点B作x轴的垂线,与双曲线 交于点C.且AB=AC,则k的值为. 16. 如图在菱形 中, , 是 、 的交点, 是线段 上的动点(不与点 、 重合),将线段 绕点 顺时针旋转 得到线段 ,点 恰好在 边上,若要使得 ,则 的范围为.
16. 如图在菱形 中, , 是 、 的交点, 是线段 上的动点(不与点 、 重合),将线段 绕点 顺时针旋转 得到线段 ,点 恰好在 边上,若要使得 ,则 的范围为.
三、解答题
-
17.(1)、计算: .(2)、化简: .18. 为保护环境“赤子之心”环保公益中心组织1000名学生参加义务收集废旧电池的活动,下面随机抽取50名学生对收集的废旧电池数量进行统计:
废旧电池数/节
3
4
5
6
8
人数/人
10
15
12
7
6
(1)、上述数据中,废旧电池节数的众数是节,中位数是节;(2)、这次活动中,1000名学生共收集废旧电池多少节?19. 在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.(1)、从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,刚好是男生的概率为 ;(2)、分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.20. 现有一块质量为10kg的甲、乙两种金属的合金.用甲种金属若干与这块合金重新熔炼,所得的新合金中甲种金属占3份,乙种金属占2份,如果再用相同数量的甲种金属与新合金重新熔炼,那么所得合金中甲种金属占7份,乙种金属占3份.求每次所用的甲种金属的质量.21. 港珠澳大桥,从2009年开工建造,于2018年10月24日正式通车.其全长55公里,连接港珠澳三地,集桥、岛、隧于一体,是世界上最长的跨海大桥.如图是港珠澳大桥的海豚塔部分效果图,为了测得海豚塔斜拉索顶端A距离海平面的高度,先测出斜拉索底端C到桥塔的距离(CD的长)约为100米,又在C点测得A点的仰角为30°,测得B点的俯角为20°,求斜拉索顶端A点到海平面B点的距离(AB的长).(已知 ≈1.73,tan20°≈0.36,结果精确到0.1) 22. 如图,一次函数 的图象与反比例函数 的图象相交于 , 两点直线 分别交 轴、 轴于 、 两点.
22. 如图,一次函数 的图象与反比例函数 的图象相交于 , 两点直线 分别交 轴、 轴于 、 两点.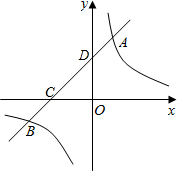 (1)、直接写出不等式 的解集;(2)、求 的值;(3)、求 点的坐标.23. 已知:如图1, 中, .
(1)、直接写出不等式 的解集;(2)、求 的值;(3)、求 点的坐标.23. 已知:如图1, 中, . (1)、请你以 为一边,在 的同侧构造一个与 全等的三角形 ,画出图形;(要求:尺规作图,保留作图痕迹,不写作法)(2)、参考(1)中构造全等三角形的方法解决下面问题:
(1)、请你以 为一边,在 的同侧构造一个与 全等的三角形 ,画出图形;(要求:尺规作图,保留作图痕迹,不写作法)(2)、参考(1)中构造全等三角形的方法解决下面问题:如图2,在四边形 中① ;② ;③ .请在上述三条信息中选择其中两条作为条件,其余的一条信息作为结论组成一个命题.试判断这个命题是否正确,并说明理由你选择的条件是__▲_,结论是_▲(只要填写序号)
24. 如图, 是 的直径, 交 于点 , 是弧 的中点, 与 交于点 , .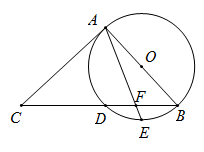 (1)、求证: 是 的切线;(2)、若 , ,求 的长.25. (阅读理解)设点 在矩形 内部,当点 到矩形的一条边的两个端点距离相等时,称点 为该边的“和谐点”例如:如图1矩形 中,若 ,则称 为边 的“和谐点”.
(1)、求证: 是 的切线;(2)、若 , ,求 的长.25. (阅读理解)设点 在矩形 内部,当点 到矩形的一条边的两个端点距离相等时,称点 为该边的“和谐点”例如:如图1矩形 中,若 ,则称 为边 的“和谐点”.
(解题运用)已知点 在矩形 内部,且 , .
(1)、设 是边 的“和谐点”,则 边 的“和谐点”(填“是”或“不是”);(2)、若 是边 的“和谐点”连接 , ,当 时,求 的长度;(3)、如图2,若 是边 的和谐点”,连接 , , ,求 的最大值.26. 已知抛物线 与 轴交于点 、 两点.
 (1)、求抛物线的解析式;(2)、当点 在抛物线上时
(1)、求抛物线的解析式;(2)、当点 在抛物线上时①如图1,过点 且不与坐标轴平行的直线 与抛物线有且只有一个交点,求直线 的方程;
②如图2若直线 与抛物线的一个交点为 ,点 在点 的右侧,过点 作 轴交直线 于点 ,延长 到点 使得 ,试判断点 是否在抛物线上?请说明理由.