江苏省南京市玄武区2021年数学中考一模试卷
试卷更新日期:2021-06-01 类型:中考模拟
一、单选题
-
1. 2021年3月15日,南京市鸡鸣寺樱花大道约有61800人前来赏樱,用科学记数法表示61800是( )A、 B、 C、 D、2. 下列计算中,结果是 的是( )A、 B、 C、 D、3. 实数 , 在数轴上对应的点的位置如图所示,下列结论正确的是( )
 A、 B、 C、 D、4. 如图,点 , , 在 上, , ,则 的度数为( )
A、 B、 C、 D、4. 如图,点 , , 在 上, , ,则 的度数为( ) A、 B、 C、 D、5. 如图,在 中, 是 边上一点,在 边上求作一点 ,使得 .甲的作法:过点 作 ,交 于点 ,则点 即为所求.乙的作法:经过点 , , 作 ,交 于点 ,则点 即为所求.对于甲、乙的作法,下列判断正确的是( )
A、 B、 C、 D、5. 如图,在 中, 是 边上一点,在 边上求作一点 ,使得 .甲的作法:过点 作 ,交 于点 ,则点 即为所求.乙的作法:经过点 , , 作 ,交 于点 ,则点 即为所求.对于甲、乙的作法,下列判断正确的是( ) A、甲错误,乙正确 B、甲正确,乙错误 C、甲、乙都错误 D、甲、乙都正确6. 已知一次函数 ( , 为常数, ), ( , 为常数, )的图象如图所示,则函数 的图象可能是( )
A、甲错误,乙正确 B、甲正确,乙错误 C、甲、乙都错误 D、甲、乙都正确6. 已知一次函数 ( , 为常数, ), ( , 为常数, )的图象如图所示,则函数 的图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
7. -3的相反数是; 的倒数是.8. 若式子 在实数范围内有意义,则x的取值范围是 .
9. 分解因式: .
10. 计算 的结果是 .
11. 设 , 是关于 的方程 的两个根,且 ,则 .12. 圆锥的底面圆的半径是3,其母线长是9,则圆锥侧面展开图的扇形的圆心角度数是.13. 如图,在正五边形 中, 是 的中点,连接 , ,则 的度数是. 14. 如图,点 , 在反比例函数 的图象上,点 在反比例函数 的图象上,连接 , ,且 轴, 轴, .若点 的横坐标为2,则 的值为.
14. 如图,点 , 在反比例函数 的图象上,点 在反比例函数 的图象上,连接 , ,且 轴, 轴, .若点 的横坐标为2,则 的值为. 15. 如图,在矩形 中, , , , 分别是 , 边上的点,若 经过点 ,且与 , 分别相切于点 , ,则 的半径为.
15. 如图,在矩形 中, , , , 分别是 , 边上的点,若 经过点 ,且与 , 分别相切于点 , ,则 的半径为. 16. 如图,在菱形 中, 是 的中点,连接 , ,将 沿直线 翻折,使得点 落在 上的点 处,连接 并延长交 于点 ,则 的值为.
16. 如图,在菱形 中, 是 的中点,连接 , ,将 沿直线 翻折,使得点 落在 上的点 处,连接 并延长交 于点 ,则 的值为.
三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 解不等式组 ,并写出它的正整数解.19. 八年级学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了20分后,其余同学乘汽车出发,结果他们同时到达,已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度.20. 随机抽取小明家一年中5个月的月用水量(单位:吨),并对当地当年月平均气温(单位: )进行了统计,得到下列统计图.
 (1)、小明家这5个月的月平均用水量为吨.(2)、下列四个推断:
(1)、小明家这5个月的月平均用水量为吨.(2)、下列四个推断:①当地当年月平均气温的极差为 ;
②当地当年月平均气温的中位数为 ;
③当地当年月平均气温的平均数在 之间;
④小明家这5个月的月用水量随着月平均气温的变化而变化,温度越高,月用水量越大.
所有合理推断的序号是.
(3)、如果用小明家5月、7月、8月这三个月的月平均用水量估计当年的用水总量,你认为是否合理?并说明理由.21. 一个 的棋盘,在棋盘方格内随机放入棋子,且每一方格内最多放入一枚棋子. (1)、如图①,棋盘内已有两枚棋子,在剩余的方格内随机放入一枚棋子,这三枚棋子恰好能在同一条直线上的概率为;(2)、如图②,棋盘内已有四枚棋子,在剩余的方格内随机放入两枚棋子,求仅有三枚棋子恰好能在同一条直线上的概率.22. 如图,在平行四边形 中, , 是对角线 上的点,且 ,连接 , .
(1)、如图①,棋盘内已有两枚棋子,在剩余的方格内随机放入一枚棋子,这三枚棋子恰好能在同一条直线上的概率为;(2)、如图②,棋盘内已有四枚棋子,在剩余的方格内随机放入两枚棋子,求仅有三枚棋子恰好能在同一条直线上的概率.22. 如图,在平行四边形 中, , 是对角线 上的点,且 ,连接 , .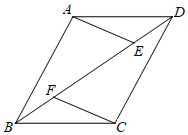 (1)、求证 ;(2)、连接 , ,若 ,求证:四边形 是菱形.23. 如图,某电影院的观众席成“阶梯状”,每一级台阶的水平宽度都为 ,垂直高度都为 .测得在 点的仰角 ,测得在 点的仰角 .求银幕 的高度.(参考数据: , , , , , )
(1)、求证 ;(2)、连接 , ,若 ,求证:四边形 是菱形.23. 如图,某电影院的观众席成“阶梯状”,每一级台阶的水平宽度都为 ,垂直高度都为 .测得在 点的仰角 ,测得在 点的仰角 .求银幕 的高度.(参考数据: , , , , , )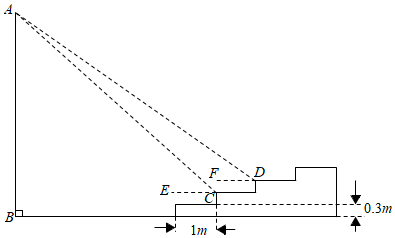 24. 某早餐机开机后,自动启动程序:先匀速加热,当机内温度升高到 时,自动停止加热,同时机内温度匀速下降,当机内温度降至 时,早餐机又自动启动上述程序,直至关机.已知早餐机的机内初始温度为 ,降温温度是加热速度的2倍.早餐机的机内温度 与开机之后的时间 之间的函数关系部分图象如图所示.
24. 某早餐机开机后,自动启动程序:先匀速加热,当机内温度升高到 时,自动停止加热,同时机内温度匀速下降,当机内温度降至 时,早餐机又自动启动上述程序,直至关机.已知早餐机的机内初始温度为 ,降温温度是加热速度的2倍.早餐机的机内温度 与开机之后的时间 之间的函数关系部分图象如图所示. (1)、早餐机的加热速度为 ;(2)、求线段 所表示的 与 之间的函数表达式;(3)、将食物放入该早餐机,自开机之后,要使机内温度不低于 的累计时间不少于 ,至少需要 .25. 已知二次函数 ( 是常数).(1)、若该函数图象与 轴有两个不同的公共点,求 的取值范围;(2)、求证:不论 为何值,该函数图象的顶点都在函数 的图象上;(3)、 , 是该二次函数图象上的点,当 时,都有 ,则 的取值范围是.26. 如图,在 中, 是 边上的点,过点 作 交 边于点 ,垂足为 ,过点 作 ,垂足为 ,连接 ,经过点 , , 的 与边 另一个公共点为 .
(1)、早餐机的加热速度为 ;(2)、求线段 所表示的 与 之间的函数表达式;(3)、将食物放入该早餐机,自开机之后,要使机内温度不低于 的累计时间不少于 ,至少需要 .25. 已知二次函数 ( 是常数).(1)、若该函数图象与 轴有两个不同的公共点,求 的取值范围;(2)、求证:不论 为何值,该函数图象的顶点都在函数 的图象上;(3)、 , 是该二次函数图象上的点,当 时,都有 ,则 的取值范围是.26. 如图,在 中, 是 边上的点,过点 作 交 边于点 ,垂足为 ,过点 作 ,垂足为 ,连接 ,经过点 , , 的 与边 另一个公共点为 . (1)、连接 ,求证 ;(2)、若 , , .
(1)、连接 ,求证 ;(2)、若 , , .①当 时,求 的半径;
②当点 在 边上运动时, 半径的最小值为 ▲ .
27. 八上教材给出了命题“如果 , , 分别是 和 的高,那么 ”的证明,由此进一步思考……(问题提出)
(1)、在 和 中, , 分别是 和 的高,如果 , , ,那么 和 全等吗?(i)小红的思考
如图,先任意画出一个 ,然后按下列作法,作出一个满足条件的 ,作法如下:

①作 的外接圆
②过点 作 ,与 交于点
③连接 (点 与 重合), (点 与 重合),得到
请说明小红所作的 .
(ii)小明的思考
如图,对于满足条件的 , 和高 , ;小明将 通过图形的变换,使边 与 重合, , 相交于点 ,连接 ,易证

接下来,小明的证明途径可以用下面的框图表示,请填写其中的空格.
 (2)、小明解决了问题(1)后,继续探索,提出了下面的问题,请你证明.
(2)、小明解决了问题(1)后,继续探索,提出了下面的问题,请你证明.如图,在 和 中, , 分别是 和 的高,( ),且 , ,求证: .
