湖南省永州市江华县2021年数学中考一模试卷

试卷更新日期：2021-06-01 类型：中考模拟

进入出卷网下载

一、单选题

1. 有理数2021的相反数为（）

A、2021 B、-2021 C、 $- \frac{1}{2020}$ D、 $\frac{1}{2020}$

查看试题解析
2. 下列计算正确的是（）

A、 $a^{3} - a^{2} = a$ B、 $a^{2} \cdot a^{3} = a$ C、 ${(3 a)}^{3} = 9 a^{3}$ D、 ${(a^{2})}^{2} = a^{4}$

查看试题解析
3. 在解方程 $\frac{x - 1}{3} + x = \frac{3 x + 1}{2}$ 时，方程两边同时乘以6，去分母后，正确的是（）

A、2x﹣1+6x=3（3x+1） B、2（x﹣1）+6x=3（3x+1） C、2（x﹣1）+x=3（3x+1） D、（x﹣1）+x=3（x+1）

查看试题解析
4. 若反比例函数 $y = \frac{k}{x}$ 的图象经过点（1，4），则此反比例函数图象经过（）

A、第一、三象限 B、第一、二象限 C、第二、四象限 D、第三、四象限

查看试题解析
5. 一元二次方程 $2021 x^{2} - x + 2021 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
6. 若一次函数y=ax+b的图象经过第一、二、四象限，则下列不等式中总是成立的是（）

A、ab＞0 B、a﹣b＞0 C、a²+b＞0 D、a+b＞0

查看试题解析
7. 在△ABC中，∠C=90°，BC=2，sinA= $\frac{2}{3}$ ，则边AC的长是（）

A、 $\sqrt{5}$ B、3 C、 $\frac{4}{3}$ D、 $\sqrt{13}$

查看试题解析
8. 数据2021， 2021， 2021， 2021 ， 2021， 2021， 2021， 2021的方差是（）

A、2021 B、0 C、－2021 D、2020

查看试题解析
9. 在求解一元二次方程－2x²＋4x＋1＝0的两个根x₁和x₂时，某同学使用电脑绘制了如图所示的二次函数y＝－2x²＋4x＋1的图象，然后通过观察抛物线与x轴的交点，该同学得出－1<x₁<0，2<x₂<3的结论，该同学采用的方法体现的数学思想是（）

A、类比 B、演绎 C、数形结合 D、整体思想

查看试题解析
10. 方程 $x^{3} - 4 x = 0$ 的解是（）

A、2或0 B、±2或0 C、2 D、－2或0

查看试题解析

二、填空题

11. 截止2021年3月19日，美国新冠疫情累计确诊人数达3035880人，请把数3035880用科学记数法表示为

查看试题解析
12. 抛物线 $y = 2 {(x + 3)}^{2} - 3$ 的开口方向为向

查看试题解析
13. 小华从斜坡底端沿斜坡走了100米后，他的垂直高度升高了50米，那么该斜坡的坡角为度

查看试题解析
14. 把一元二次方程5x（x-3）=6-2x化成一般形式后常数项是

查看试题解析
15. 不等式组 ${\begin{cases} x + 2 > 1 \\ 2 x - 1 \leq 8 - x \end{cases}$ 的最大整数解是．

查看试题解析
16. 已知△ABC的三边分别是5，6，7，则与它相似△ $A^{'} B^{'} C^{'}$ 的最短边为10，则△ $A^{'} B^{'} C^{'}$ 的周长是

查看试题解析
17. 在一个圆中60度的圆心角所对的弧长为 $\frac{2}{3} π$ ，则该圆的直径为

查看试题解析
18. 符号“ $f$ ”表示一种运算，它对一些数的运算如下： $f_{(1)}$ ＝1＋ $\frac{2}{1}$ ， $f_{(2)}$ ＝1＋ $\frac{2}{2}$ ， $f_{(3)}$ ＝1＋ $\frac{2}{3}$ ， $f_{(4)}$ ＝1＋ $\frac{2}{4}$ ，….利用以上运算的规律求出2021 $f_{(2021)}$ ＝

查看试题解析

三、解答题

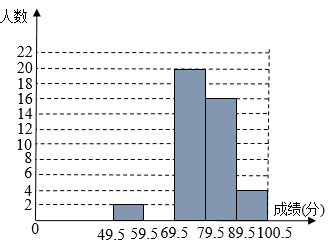
19. 计算： ${(\frac{1}{3})}^{- 1} - \sqrt{27} + 3 t a n 60^{\circ} + {(2021)}^{0}$

查看试题解析
20. 先化简，再求值：（a＋b）（a－b）＋（a＋b）² ，其中a＝－1，b＝ $\frac{1}{2}$

查看试题解析

21. 某班数学科代表小华对本班上期期末考试数学成绩作了统计分析，绘制成如下频数、频率统计表和频数分布直方图，请你根据图表提供的信息，解答下列问题：

分组	49.5～59.5	59.5～69.5	69.5～79.5	79.5～89.5	89.5～100.5	合计
频数	2	a	20	16	4	50
频率	0.04	0.16	0.40	0.32	b	1

(1)、频数、频率统计表中，a= ；b= ；

(2)、请将频数分布直方图补充完整；

(3)、小华在班上任选一名同学，该同学成绩不低于80分的概率是多少？

查看试题解析

22. 如图，在平行四边形ABCD中，AB=3，AD= $4 \sqrt{2}$ ，AF交BC于E，交DC的延长线于F，且CF=1，求CE的长

查看试题解析
23. 如图，△ABC为等边三角形，D、F分别为BC、AB上的点，且CD＝BF，以AD为边作等边△ADE．

(1)、求证：△ACD≌△CBF；

(2)、点D在线段BC上何处时，四边形CDEF是平行四边形且 $∠ D E F = 30^{o}$ ．

查看试题解析
24. 如图，在Rt△ABC中，∠ACB＝90°，AO是△ABC的角平分线.以O为圆心，OC为半径作⊙O.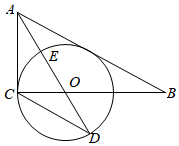

(1)、求证：AB是⊙O的切线.

(2)、已知AO交⊙O于点E，延长AO交⊙O于点D，tan∠ADC＝ $\frac{2}{3}$ ，求 $\frac{A E}{A C}$ 的值.

查看试题解析

25. 永州四中组织师生共60人，从永州乘高铁前往祁阳一中参加学习交流活动，高铁票价格如下表所示：（教师按成人票价购买，学生按学生票价购买）

运行区间	成人票价（元/张）	成人票价（元/张）	成人	学生
出发站	终点站	一等座	二等座	二等座
永州	祁阳	30	20	10

若师生均购买二等座票，则共需700元.

(1)、求参加活动的教师和学生各有多少人？

(2)、由于部分教师需提早前往做准备工作，这部分教师均购买一等座票，而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人，购买一、二等座票全部费用为y元.

①求y关于x的函数关系式；

②若购买一、二等座票全部费用不多于1200元，则提早前往的教师最多只能多少人？

查看试题解析

26. 如图，已知抛物线y＝ax²＋bx＋c（a≠0）的对称轴为直线x＝－1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B.

(1)、求抛物线的解析式

(2)、若直线y＝mx＋n经过B、C两点，求直线BC的解析式；

(3)、在抛物线的对称轴x＝－1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标及此时距离之和的最小值

查看试题解析