湖北省武汉市九年级2021年数学4月调考模拟试卷(1)
试卷更新日期:2021-06-01 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、2 C、 D、2. 一个不透明的口袋中装有四个相同的小球,它们分别标号为 , , , .从中同时摸出两个,则下列事件为随机事件的是( )A、两个小球的标号之和等于 B、两个小球的标号之和大于 C、两个小球的标号之和等于 D、两个小球的标号之和大于3. 下列四个图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图是由5个相同的小正方体搭成的几何体,它的左视图是( )
4. 如图是由5个相同的小正方体搭成的几何体,它的左视图是( ) A、
A、 B、
B、 C、
C、 D、
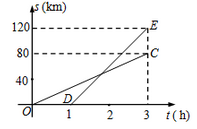
D、 5. 有两把不同的锁和三把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁.现在任意取出一把钥匙去开任意一把锁,则一次打开锁的概率是( )A、 B、 C、 D、6. 已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图中DE,OC分别表示甲、乙离开A地的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象,设在这个过程中,甲、乙两人相距y(单位:千米),则y关于t的函数图象是( )
5. 有两把不同的锁和三把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁.现在任意取出一把钥匙去开任意一把锁,则一次打开锁的概率是( )A、 B、 C、 D、6. 已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图中DE,OC分别表示甲、乙离开A地的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象,设在这个过程中,甲、乙两人相距y(单位:千米),则y关于t的函数图象是( )
 A、
A、 B、
B、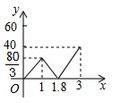 C、
C、 D、
D、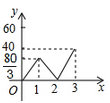 7. 如图,一次函数 与反比例函数 的图象交于点 , .则关于 的不等式 的解集是( )
7. 如图,一次函数 与反比例函数 的图象交于点 , .则关于 的不等式 的解集是( ) A、 ,或 B、 ,或 C、 ,或 D、 ,或8. 如图,从圆外一点 引圆的两条切线 , , , 为切点, 为 上的一点,连接 交 于点 ,若 , , ,则 的半径长是( )
A、 ,或 B、 ,或 C、 ,或 D、 ,或8. 如图,从圆外一点 引圆的两条切线 , , , 为切点, 为 上的一点,连接 交 于点 ,若 , , ,则 的半径长是( ) A、 B、 C、 D、9. 在平面直角坐标系中,我们把横纵坐标均为整数的点称为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.例如:图中 的与四边形 均为格点多边形.格点多边形的面积记为 ,其内部的格点数记为 ,边界上的格点记为 ,已知格点多边形的面积可表示为 ( , 为常数),若某格点多边形对应的 , ,则 ( )
A、 B、 C、 D、9. 在平面直角坐标系中,我们把横纵坐标均为整数的点称为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.例如:图中 的与四边形 均为格点多边形.格点多边形的面积记为 ,其内部的格点数记为 ,边界上的格点记为 ,已知格点多边形的面积可表示为 ( , 为常数),若某格点多边形对应的 , ,则 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 计算 的结果是.11. 在2021年元旦汇演中, 位评委给八年级一班的参赛节目打分如表格:
成绩/分
评委人数
则这组数据的众数是 .
12. 计算 的结果是.13. 如图.将 绕点 逆时针旋转 得到 ,连接 ,若 ,则 的度数是. 14. 如图,在 中, ,点 在 上,点 为 外一点,且 为等边三角形, ,若 , ,则 的边长为.
14. 如图,在 中, ,点 在 上,点 为 外一点,且 为等边三角形, ,若 , ,则 的边长为. 15. 抛物线 的顶点为 ,与 轴的一个交点 在点 和 之间,则以下结论:① ;② ;③ ;④方程 有两个不相等的实数根,其中正确结论为.
15. 抛物线 的顶点为 ,与 轴的一个交点 在点 和 之间,则以下结论:① ;② ;③ ;④方程 有两个不相等的实数根,其中正确结论为.三、解答题
-
16. 计算: .17. 如图,四边形 中, ,点 在 边上, 于点 , ,求证: .
 18. 小明同学想了解本校九年级学生对哪门课程感兴趣,随机抽取了部分九年级学生进行调查(每名学生只能选择一门课程).将获得的数据整理绘制成如图两幅不完整的统计图.
18. 小明同学想了解本校九年级学生对哪门课程感兴趣,随机抽取了部分九年级学生进行调查(每名学生只能选择一门课程).将获得的数据整理绘制成如图两幅不完整的统计图.

根据统计图提供的信息,解答下列问题:
(1)、 的值是 ,扇形统计图中,“数学”所对应的圆心角度数是度;(2)、请补全条形统计图;(3)、若该校九年级共有 名学生,请你估计该校九年级学生中大约有多少名学生对数学感兴趣?19. 如图是由边长为 的小正方形构成的网格.每个小正方形的顶点叫做格点. 的顶点在格点上,仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题: (1)、将边 绕点 逆时针旋转 得到线段 ;(2)、画 的高 ;(3)、将点 竖直向下平移 个单位长度得到点 ,画出点 ;(4)、画线段 关于直线 的对称线段 .20. 如图,从 外一点 引割线 , 与 相切于点 ,连接 , , .
(1)、将边 绕点 逆时针旋转 得到线段 ;(2)、画 的高 ;(3)、将点 竖直向下平移 个单位长度得到点 ,画出点 ;(4)、画线段 关于直线 的对称线段 .20. 如图,从 外一点 引割线 , 与 相切于点 ,连接 , , .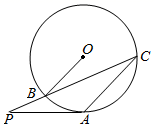 (1)、求证: ;(2)、已知 , ,求 的长.21. 受“新冠”疫情的影响,某销售商在网上销售A、B两种型号的“手写板”,获利颇丰.已知A型,B型手写板进价、售价和每日销量如表格所示:
(1)、求证: ;(2)、已知 , ,求 的长.21. 受“新冠”疫情的影响,某销售商在网上销售A、B两种型号的“手写板”,获利颇丰.已知A型,B型手写板进价、售价和每日销量如表格所示:进价(元/个)
售价(元/个)
销量(个/日)
A型
600
900
200
B型
800
1200
400
根据市场行情,该销售商对A手写板降价销售,同时对B手写板提高售价, 此时发现A手写板每降低5元就可多卖1个,B手写板每提高5元就少卖1个, 要保持每天销售总量不变,设其中A手写板每天多销售x,每天总获利的利润为y
(1)、求y、x间的函数关系式并写出x取值范围;(2)、要使每天的利润不低于234000元,直接写出x的取值范围;(3)、该销售商决定每销售一个B手写板,就捐a元给 因“新冠疫情”影响的困难家庭,当 时,每天的最大利润为229200元,求a的值.22. (1)、[问题背景]如图1, 是等腰直角三角形, ,直线 过点 , , ,垂足分别为 , .求证: ;(2)、[尝试应用]如图2, , , , , 三点共线, , , , .求 的长;(3)、[拓展创新]如图3,在 中, ,点 , 分别在 , 上, , ,若 ,直接写出 的值为.23. 如图1,抛物线 交 轴于 , 两点( 在 的左侧),与 轴交于点 ,且 .
(1)、[问题背景]如图1, 是等腰直角三角形, ,直线 过点 , , ,垂足分别为 , .求证: ;(2)、[尝试应用]如图2, , , , , 三点共线, , , , .求 的长;(3)、[拓展创新]如图3,在 中, ,点 , 分别在 , 上, , ,若 ,直接写出 的值为.23. 如图1,抛物线 交 轴于 , 两点( 在 的左侧),与 轴交于点 ,且 . (1)、求抛物线的解析式;(2)、连接 , ,点 在抛物线上,且满足 ,求点 的坐标;(3)、如图2,直线 交 轴于点 ,过直线 上的一动点 作 轴交抛物线于点 ,直线 交抛物线于另一点 ,直线 交 轴于点 ,试求 的值.
(1)、求抛物线的解析式;(2)、连接 , ,点 在抛物线上,且满足 ,求点 的坐标;(3)、如图2,直线 交 轴于点 ,过直线 上的一动点 作 轴交抛物线于点 ,直线 交抛物线于另一点 ,直线 交 轴于点 ,试求 的值.