湖北省黄冈市2021年数学中考二模试卷
试卷更新日期:2021-06-01 类型:中考模拟
一、单选题
-
1. 2的相反数是( )A、 2 B、 C、 D、2. 永州市现有户籍人口约635.3万人,则“现有户籍人口数”用科学记数法表示正确的是( )A、 人 B、 人 C、 人 D、3. 如图, , , ,则 的度数是( )
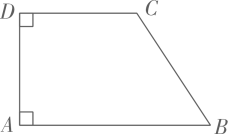 A、 B、 C、 D、4. 如图所示的几何体,从上面看得到的图形是( )
A、 B、 C、 D、4. 如图所示的几何体,从上面看得到的图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 下列计算正确的是( )A、 B、 C、 D、6. 小明根据朗诵比赛中9位评委给出的分数,制作了此表,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
5. 下列计算正确的是( )A、 B、 C、 D、6. 小明根据朗诵比赛中9位评委给出的分数,制作了此表,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )平均数
中位数
众数
方差
82
83
84
0.35
A、平均数 B、中位数 C、众数 D、方差7. 如图,菱形 中,过顶点 作 交对角线 于 点,已知 ,则 的大小为( )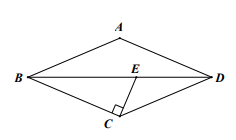 A、 B、 C、 D、8. 若定义一种新运算: 例如: ; .则函数 的图象大致是( )A、
A、 B、 C、 D、8. 若定义一种新运算: 例如: ; .则函数 的图象大致是( )A、 B、
B、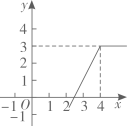 C、
C、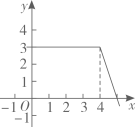 D、
D、
二、填空题
-
9. 计算: .10. 关于 的某个不等式组的解集在数轴上表示如图所示,则该不等式组的解集为.
 11. 已知 是方程 的两个实数根,则式子 的值为.12. 《九章算术》是我国传统数学中重要的著作之一,奠定了我国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”大意:有一扇形状是矩形的门,它的高比宽多6尺8寸,它的对角线长1丈,那么门的高为尺.(1丈=10尺,1尺=10寸)
11. 已知 是方程 的两个实数根,则式子 的值为.12. 《九章算术》是我国传统数学中重要的著作之一,奠定了我国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”大意:有一扇形状是矩形的门,它的高比宽多6尺8寸,它的对角线长1丈,那么门的高为尺.(1丈=10尺,1尺=10寸) 13. 在线上教学期间,某校落实市教育局要求,督促学生每天做眼保健操.为了解落实情况,学校随机抽取了部分学生进行调查,调查结果分为四类(A类:总时长 分钟;B类:5分钟 总时长 分钟;C类:10分钟 总时长 分钟;D类:总时长 15分钟),将调查所得数据整理并绘制成如下两幅不完整的统计图.
13. 在线上教学期间,某校落实市教育局要求,督促学生每天做眼保健操.为了解落实情况,学校随机抽取了部分学生进行调查,调查结果分为四类(A类:总时长 分钟;B类:5分钟 总时长 分钟;C类:10分钟 总时长 分钟;D类:总时长 15分钟),将调查所得数据整理并绘制成如下两幅不完整的统计图.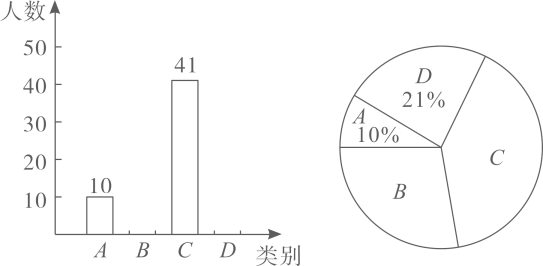
该校共有1200名学生,请根据以上统计分析,估计该校每天做眼保健操总时长超过5分钟且不超过10分钟的学生约有人.
14. 如图,在 中, , ,点 是 的中点,连接 ,将 沿射线 方向平移,在此过程中, 的边 与 的边 、 分别交于点 、 ,当 的面积是 面积的 时,则△BCD 平移的距离是. 15. 如图,已知 的半径为2,弦 ,点 为优弧 上动点,点 为 的内心,当点 从点 向点 运动时,点 移动的路径长为.
15. 如图,已知 的半径为2,弦 ,点 为优弧 上动点,点 为 的内心,当点 从点 向点 运动时,点 移动的路径长为. 16. 如图,无人机于空中 处测得某建筑顶部 处的仰角为45°,测得该建筑底部 处的俯角为35°.若无人机的飞行高度 为42m,则该建筑的高度 为 .(参考数据: , , ).
16. 如图,无人机于空中 处测得某建筑顶部 处的仰角为45°,测得该建筑底部 处的俯角为35°.若无人机的飞行高度 为42m,则该建筑的高度 为 .(参考数据: , , ).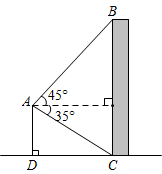
三、解答题
-
17. 计算: .18. 如图,已知点D、E是△ABC内两点,且∠BAE=∠CAD,AB=AC,AD=AE.
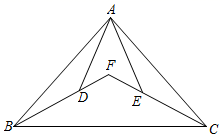 (1)、求证: .(2)、延长BD、CE交于点F,若 , ,求 的度数.19. 在一个不透明的口袋中装有4个依次写有数字1,2,3,4的小球,它们除数字外其余都相同,每次摸球前都将小球摇匀.(1)、从中随机摸出一个小球,求上面的数字不小于3的概率.(2)、从中随机摸出一个球后不放回,再随机摸出一个球,请用列表或画树状图的方法,求两次摸出小球上的数字之和恰好是偶数的概率.20. 如图:直线AB与双曲线y= 点交于A、B两点,直线AB与x、y坐标轴分别交于C、D两点,连接OA,若OA=2 ,tan∠AOC= ,B(3,m)
(1)、求证: .(2)、延长BD、CE交于点F,若 , ,求 的度数.19. 在一个不透明的口袋中装有4个依次写有数字1,2,3,4的小球,它们除数字外其余都相同,每次摸球前都将小球摇匀.(1)、从中随机摸出一个小球,求上面的数字不小于3的概率.(2)、从中随机摸出一个球后不放回,再随机摸出一个球,请用列表或画树状图的方法,求两次摸出小球上的数字之和恰好是偶数的概率.20. 如图:直线AB与双曲线y= 点交于A、B两点,直线AB与x、y坐标轴分别交于C、D两点,连接OA,若OA=2 ,tan∠AOC= ,B(3,m) (1)、求一次函数与反比例函数解析式;(2)、若点F是点D关于x轴的对称点,求△ABF的面积.21. 如图,已知 是 的直径, 是 上的一点, 是 上的一点, 于 , 交 于 ,且 .
(1)、求一次函数与反比例函数解析式;(2)、若点F是点D关于x轴的对称点,求△ABF的面积.21. 如图,已知 是 的直径, 是 上的一点, 是 上的一点, 于 , 交 于 ,且 . (1)、求证: 是 的切线;(2)、若 , ,圆的半径 ,求切线 的长.22. “中华紫薇园”景区今年“五一”期间开始营业,为方便游客在园区内游玩休息,决定向一家园艺公司采购一批户外休闲椅,经了解,公司出售两种型号休闲椅,如下表:
(1)、求证: 是 的切线;(2)、若 , ,圆的半径 ,求切线 的长.22. “中华紫薇园”景区今年“五一”期间开始营业,为方便游客在园区内游玩休息,决定向一家园艺公司采购一批户外休闲椅,经了解,公司出售两种型号休闲椅,如下表:可供使用人数(人/条)
价格(元/条)
长条椅
3
160
弧形椅
5
200
景区采购这批休闲椅共用去56000元,购得的椅子正好可让1300名游客同时使用.
(1)、求景区采购了多少条长条椅,多少条弧形椅?
(2)、景区现计划租用A、B两种型号的卡车共20辆将这批椅子运回景区,已知A型卡车每辆可同时装运4条长条椅和11条弧形椅,B型卡车每辆可同时装运12条长条椅和7条弧形椅.如何安排A、B两种卡车可一次性将这批休闲椅运回来?
(3)、又知A型卡车每辆的运费为1200元,B型卡车每辆的运费为1050元,在(2)的条件下,若要使此次运费最少,应采取哪种方案?并求出最少的运费为多少元.
23. 某水果店销售某种水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价 (元)与销售时间第 月之间存在如图1(一条线段)所示的变化趋势,每千克成本 (元)与销售时间第 月之间存在如图2(一段抛物线,对称轴为直线 )所示的变化趋势.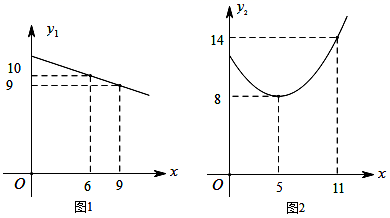 (1)、分别求函数 和 的表达式;(2)、销售这种水果,第几月每千克所获得利润最大?最大利润是多少?24. 如图,抛物线y=ax2+bx+2(a<0)与x轴交于点A(﹣1,0)和点B(2,0),与y轴交于点C.
(1)、分别求函数 和 的表达式;(2)、销售这种水果,第几月每千克所获得利润最大?最大利润是多少?24. 如图,抛物线y=ax2+bx+2(a<0)与x轴交于点A(﹣1,0)和点B(2,0),与y轴交于点C.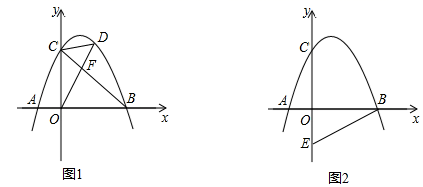 (1)、求该抛物线的函数解析式;(2)、如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD、CD,OD交BC于点F,当S△COF:S△CDF=2:1时,求点D的坐标;(3)、如图2,点E的坐标为(0,﹣1),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
(1)、求该抛物线的函数解析式;(2)、如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD、CD,OD交BC于点F,当S△COF:S△CDF=2:1时,求点D的坐标;(3)、如图2,点E的坐标为(0,﹣1),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.