湖北省恩施市2021年数学中考第一次适应性考试试卷

试卷更新日期：2021-06-01 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2035的绝对值是（）

A、﹣2035 B、2035 C、±2035 D、 $\frac{1}{2035}$

查看试题解析
2. 2020年11月第七次全国人口普查正式开启现场登记，约 $7000000$ 普查人员走入千家万户.数据 $7000000$ 用科学记数法可表示为（）

A、 $0.7 \times 10^{7}$ B、 $7 \times 10^{7}$ C、 $7 \times 10^{6}$ D、 $70 \times 10^{5}$

查看试题解析
3. 下列运算正确的是（）

A、 $3 a^{2} - a^{2} = 3$ B、 ${(a + b)}^{2} = a^{2} + b^{2}$ C、 ${(- 3 a b^{2})}^{2} = 6 a^{2} b^{4}$ D、 $a^{2} \cdot a^{4} = a^{6}$

查看试题解析
4. 自2019年底，我市全面铺开市区生活垃圾分类工作，分门别类打造适合恩施实际的生活垃圾分类处置体系.将垃圾分为可回收物、厨余垃圾（含餐厨垃圾）、有害垃圾、其他垃圾.以下图标是几类垃圾的标志，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 如图所示，把一个长方形纸片沿 $E F$ 折叠后，点 $D$ ， $C$ 分别落在 $D^{'}$ ， $C^{'}$ 的位置.若 $∠ A E D^{'} = 50 °$ ，则 $∠ E F C$ 等于（）

A、 $65 °$ B、 $110 °$ C、 $115 °$ D、 $130 °$

查看试题解析
6. 2020年10月25日，孙琳参加学校举办的“抗美援朝70周年缅怀先烈”主题演讲比赛，她的演讲资料、语言表达、形象风度、综合印象得分分别为85分，70分，80分，80分.若依次按照40%，40%，15%，5%的百分比确定成绩，则她的成绩是（）

A、 80分 B、79分 C、78分 D、77分

查看试题解析
7. 若关于 x 的不等式组 ${\begin{array}{l} x - 2 < 0 \\ 3 x + 4 > a - x \end{array}$ 恰好只有 2 个整数解，则所有满足条件的整数 a 的值之和是（）

A、3 B、4 C、6 D、1

查看试题解析
8. 如图，是由几个相同的小正方体组成立体图形的俯视图，数字表示其位置上的小正方体的个数，则该立方体的主视图是（）

A、 B、 C、 D、

查看试题解析
9. 随着全球能源危机的逐渐加重，太阳能发电行业发展迅速全球太阳能光伏应用市场持续稳步增长，2019年全球装机总量约600GW，预计到2021年全球装机总量达到864GW.设全球新增装机量的年平均增长率为x，则x值为（）

A、20% B、30% C、40% D、50%

查看试题解析
10. 函数y＝ $\frac{\sqrt{x - 2}}{x - 1}$ 中自变量x的取值范围是（）

A、x≥2且x≠1 B、x≥2 C、x≠1 D、﹣2≤x＜1

查看试题解析
11. 如图， $M$ 是 $△ A B C$ 的边 $B C$ 的中点， $A N$ 平分 $∠ B A C$ ， $B N ⊥ A N$ 于点 $N$ ，且 $A B = 8$ ， $M N = 3$ .则 $A C$ 的长为（）

A、 $10$ B、 $12$ C、 $14$ D、 $16$

查看试题解析
12. 二次函数y＝ax²+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a），下列结论：①abc＜0；②4a+2b+c＞0；③5a﹣b+c＝0；④若方程a（x+5）（x﹣1）＝﹣1有两个根x₁和x₂ ，且x₁＜x₂ ，则﹣5＜x₁＜x₂＜1；⑤若方程|ax²+bx+c|＝1有四个根，则这四个根的和为﹣8，其中正确的结论有（）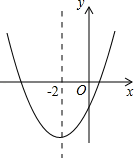

A、①②③④ B、①②③⑤ C、②③④⑤ D、①②④⑤

查看试题解析

二、填空题

13. 因式分解： $12 - 3 x^{2} =$ .

查看试题解析
14. 如图，在等腰直角三角形 $A B C$ 中， $∠ A C B = 90 °$ ， $A C = 4$ ，以 $B C$ 边中点 $D$ 为圆心， $C D$ 的长为半径作弧，交 $A B$ 于点 $E$ ，以点 $A$ 为圆心， $A C$ 的长为半径作弧交 $A B$ 于点 $F$ ，则图中阴影部分的面积为.（用含 $π$ 的式子表示）

查看试题解析
15. 如图所示，在平面直角坐标系 $x O y$ 中，一组同心圆的圆心为坐标原点 $O$ ，它们的半径分别为1，2，3，…，按照“加1”依次递增；一组平行线， $l_{0}$ ， $l_{1}$ ， $l_{2}$ ， $l_{3}$ ，…都与x轴垂直，相邻两直线的间距为l，其中 $l_{0}$ 与 $y$ 轴重合若半径为2的圆与 $l_{1}$ 在第一象限内交于点 $P_{1}$ ，半径为3的圆与 $l_{2}$ 在第一象限内交于点 $P_{2}$ ，…，半径为 $n + 1$ 的圆与 $l_{n}$ 在第一象限内交于点 $P_{n}$ ，则点 $P_{n}$ 的坐标为．（ $n$ 为正整数）

查看试题解析

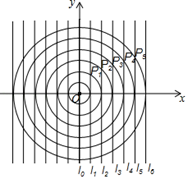
三、解答题

16. 先化简，再求值： $(\frac{x^{2} - 1}{x^{2} + x}) \div (x - \frac{2 x - 1}{x})$ ，其中. $x = \sqrt{5} + 1$ .

查看试题解析
17. 将两张完全相同的矩形纸片 $A B C D$ 、 $F B E D$ 按如图方式放置， $B D$ 为重合的对角线.重叠部分为四边形 $D H B G$ .试判断四边形 $D H B G$ 的形状，并说明理由.

查看试题解析
18. 每年5月的第二周为：“职业教育活动周”，今年某市拟展开以“弘扬工匠精神，打造技能强国”为主题的系列活动.某职业中学计划组织全校师生、学生家长和社区居民参加“职教体验观摩”活动，为安排好活动当天技术人员的现场演示，该校随机抽取了部分学生进行了前期调查：“你最感兴趣的一种职业技能是什么？”并对此进行了统计，绘制了如图所示统计图（均不完整）.

(1)、请你补全条形统计图；

(2)、若该校共有 $3000$ 名学生，请估计该校对“工艺设计”最感兴趣的学生有多少人？

(3)、据了解，该市恰在学生感兴趣的计算机技术（ $A$ ）、机电维修（ $B$ ）、服装设计（ $C$ ）、工艺设计（ $D$ ）四个领域各有一名“大国工匠”.现学校计划观摩活动结束后，从中选 $2$ 名“大国工匠”对该校学生开展一场“工匠精神”故事宣讲，求所选中“工匠”为A和C领域的概率.

查看试题解析
19. 汉书《淮南万毕术》记载：取大境高悬，置水盆于下，则见四邻.如图1，这句话是说，利用高挂上面的镜子所成的像，再反射到水盆中，借此观察院墙外景象.相关光的路径和围墙等，用几何图形表示如图2，已知点 $E$ ， $B$ ， $N$ ， $D$ 在同一条水平线上，点 $C$ 在围墙 $M N$ 的正上方， $M N ⊥ B D$ 于点 $N$ ， $A E ⊥ D B$ 于点 $E$ ， $∠ A B E = ∠ C B N = 60 °$ ， $∠ B C D = 80 °$ ， $A B = 1.6$ 米， $B N = 3 B E$ ，求点 $D$ 到墙脚 $N$ 的距离.（结果精确到 $0.1$ 米.参考数据： $\sin 50 ° \approx 0.77$ ， $\cos 50 ° \approx 0.64$ ， $\tan 50 ° \approx 1.19$ ， $\sin 80 ° \approx 0.98$ ， $\cos 80 ° \approx 0.17$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
20. 如图，在平面直角坐标系中，O为坐标原点，点A，B在函数 $y = \frac{k}{x}$ $(x > 0)$ 的图象上（点B的横坐标大于点A的横坐标），点A的坐示为 $(2 ， 4)$ ，过点A作 $A D ⊥ x$ 轴于点D，过点B作 $B C ⊥ x$ 轴于点C，连接 $O A$ ， $A B$ ．

(1)、求k的值．

(2)、若D为 $O C$ 中点，求四边形 $O A B C$ 的面积．

查看试题解析
21. 为更好践行党史学习活动，某学校计划租用汽车送部分团员学生和党员教师共 $206$ 人到革命英雄纪念馆开展党史学习教育，其中团员的人数比党员人数的 $13$ 倍还多 $10$ 人.现在甲、乙两种客车（不能超员），它们的载客量和租金如下表所示：

甲型客车

乙型客车

载客量（人/辆）

$33$

$22$

租金（元/辆）

$300$

$200$

为确保安全，学校规定：每辆车上至少要有 $2$ 名教师.如果学校预算此次活动的租金总费用不超过 $2000$ 元，请解答下列问题：

(1)、参加此次活动的团员和党员各多少人？

(2)、设租用 $x$ 辆甲种客车，租车总费用为 $y$ 元.
①学校共有哪几种租车方案？

②写出 $y$ 与 $x$ 的函数关系式，并求租车总费用 $y$ 的最小值.

查看试题解析
22. 如图， $P A$ 为 $⊙ O$ 的切线， $A$ 为切点，过 $A$ 作 $O P$ 的垂线 $A B$ ，垂足为点 $C$ ，交 $⊙ O$ 于点 $B$ .连接 $B O$ 并延长交 $⊙ O$ 于点 $D$ ，交 $P A$ 的延长线于点 $E$ .

(1)、求证： $P B$ 为 $⊙ O$ 的切线；

(2)、若 $A E = 5$ ， $D E = 3$ ，求 $⊙ O$ 的半径；

(3)、若 $O C ： B C = 2 ： 3$ ，求 $\sin E$ 的值.

查看试题解析
23. 如图，在平面直角坐标系 $x O y$ 中，已知直线 $y = - x - 3$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $C$ ，过 $A$ 、 $C$ 两点的抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴交于另一点 $B (1 ， 0)$ ，抛物线对称轴为直线 $l$ .

(1)、求抛物线的解析式；

(2)、点 $M$ 为直线 $A C$ 下方抛物线上一点，当 $△ M A C$ 的面积最大时，求点 $M$ 的坐标；

(3)、点 $P$ 是抛物线上的点，过点 $P$ 作 $l$ 的垂线，垂足为 $D$ ， $E$ 是 $l$ 上的点.要使得以 $P$ 、 $D$ 、 $E$ 为顶点的三角形与 $△ B O C$ 全等，请求出点 $P$ 、点 $E$ 的坐标；

(4)、在（2）的条件下，点 $N$ 为 $y$ 轴上一点，求 $M N + \frac{1}{2} O N$ 的最小值.

查看试题解析

	甲型客车	乙型客车
载客量（人/辆）	$33$	$22$
租金（元/辆）	$300$	$200$