湖北省丹江口市2021年初中毕业生诊断考试数学试卷

试卷更新日期：2021-06-01 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣ $\frac{1}{5}$ 的绝对值是（）

A、﹣ $\frac{1}{5}$ B、 $\frac{1}{5}$ C、﹣5 D、5

查看试题解析
2. 如图，将一块三角板的直角顶点放在直尺的一边上，当∠2＝40°时，∠1的度数为（）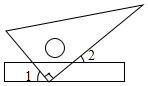

A、40° B、45° C、50° D、55°

查看试题解析
3. 五个大小相同的正方体塔成的几何体如图所示，其左视图是（）

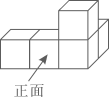A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 $3 a + 2 b = 5 a b$ B、 $a^{3} \cdot a^{2} = a^{6}$ C、 ${(- a^{3} b)}^{2} = a^{6} b^{2}$ D、 $a^{2} b^{3} + a = b^{3}$

查看试题解析
5. 某学校九年级1班九名同学参加定点投篮测试，每人投篮六次，投中的次数统计如下：4，3，5，5，2，5，3，4，1，这组数据的中位数、众数分别为（）

A、4，5 B、5，4 C、4，4 D、5，5

查看试题解析
6. 一个多边形的每个内角都是135°，则其内角和为（）

A、900° B、1080° C、1260° D、1440°

查看试题解析
7. 我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽．“其大意为：现请人代买一批椽，这批椽的价钱为6210文．如果每件椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设这批椽的数量为 $x$ 株，则符合题意的方程是（）

A、 $3 (x - 1) = \frac{6210}{x}$ B、 $\frac{6210}{x - 1} = 3$ C、 $3 x - 1 = \frac{6210}{x}$ D、 $\frac{6210}{x} = 3$

查看试题解析
8. 如图，每一幅图中均含有若干个正方形，第1幅图中有1个正方形；第2幅图中有5个正方形……按这样的规律下去，第9幅图中正方形正的个数为（）

A、180 B、204 C、285 D、385

查看试题解析
9. 如图，AB是⊙O的直径，C是⊙O上的一点，CD平分∠ACB交⊙O于点D，交AB于点E，若AC＝6，BC＝8，则 $\frac{C E}{D E}$ 的值为（）

A、 $\frac{24}{25}$ B、1 C、 $\frac{25}{24}$ D、 $\frac{12}{13}$

查看试题解析
10. 如图，A、B是双曲线y＝ $\frac{k}{x}$ 上的点，点C在x轴上，B是线段AC的中点， $S_{△ O A C} = 6$ .则k的值为（）

A、3 B、4 C、6 D、8

查看试题解析

二、填空题

11. 分解因式： $x^{2} - 9 =$ .

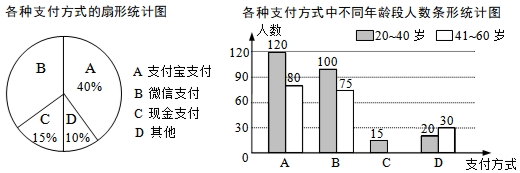
查看试题解析
12. 为了解泰山庙社区20～60岁居民最喜欢的支付方式，某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查（每人只能选择其中一项），并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息估计该社区中20～60岁的居民约10000人，估算其中41﹣60岁的人中最喜欢现金支付方式的人数为.

查看试题解析
13. 一条排水管的截面如图所示，已知排水管的半径OA＝2m，水面宽AB＝2.4m，某天下雨后，水管水面上升了0.4m，则此时排水管水面宽CD等于m.

查看试题解析
14. 某型号飞机的机翼形状如图所示，根据图中数据计算AB的长度为.（结果保留小数点后两位， $\sqrt{3}$ ≈1.732）

查看试题解析
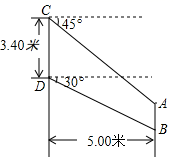15. 规定[x]为不大于x的最大整数，如[0.7]＝0，[﹣2.3]＝﹣3，若[x+0.5]＝2，且[1﹣x]＝﹣2，则x的取值范围为.

查看试题解析
16. 如图，四边形ABCD中，AB＝6 $\sqrt{2}$ ，∠ABC＝45°，E是BD上一点，若∠ABD＝15°，则AE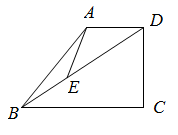+ $\frac{1}{2}$ BE的最小值为.

查看试题解析

三、解答题

17. 计算： ${(\sqrt{10} - 1)}^{0}$ ﹣|﹣3|+ $\sqrt{2}$ cos45°+ ${(\frac{1}{4})}^{- 1}$ .

查看试题解析
18. 先化简，再求值： $\frac{a^{2} - 2 a b + b^{2}}{2 a - 2 b}$ ÷（ $\frac{1}{b} - \frac{1}{a}$ ），其中a＝ $\sqrt{3}$ +1，b＝ $\sqrt{3}$ ﹣1.

查看试题解析
19. 一个箱子内有4颗相同的球，将4颗球分别标示号码1、2、3、4，今翔翔以每次从箱子内取一颗球且取后放回的方式抽取，并预计取球10次，现已取了8次，取出的结果如表所列：
次数
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
第9次
第10次
号码
1
3
4
4
2
1
4
1

若每次取球时，任一颗球被取到的机会皆相等，且取出的号码即为得分，请回答下列问题：

(1)、请求出第1次至第8次得分的平均数．

(2)、承（1），翔翔打算依计划继续从箱子取球2次，请判断是否可能发生「这10次得分的平均数不小于2.2，且不大于2.4」的情形？若有可能，请计算出发生此情形的机率，并完整写出你的解题过程；若不可能，请完整说明你的理由．

查看试题解析
20. 如图，将平行四边形ABCD折叠，使点C与点A重合，折痕EF交BC于E交AD于F，交AC于G，连接AE，CF.

(1)、求证：四边形AECF为菱形；

(2)、若四边形AECF恰为正方形，且AB＝5，BC＝7，求平行四边形ABCD的面积.

查看试题解析
21. 关于x的一元二次方程x²+2（k﹣1）x+k²﹣1＝0有实数根.

(1)、求k的取值范围；

(2)、若方程的两根x₁ ， x₂满足（x₁﹣1）（x₂﹣1）＝6，求k的值.

查看试题解析
22. 如图，AB是⊙O的直径，C是⊙O上的一点，D是AB延长线上的一点，且∠BCD＝∠A.

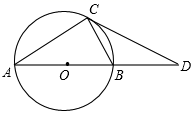(1)、求证：CD是⊙O的切线；

(2)、若AC＝8，sinA＝ $\frac{3}{5}$ ，求CD长.

查看试题解析
23. 某商店以40元/斤的单价新进一批茶叶，在销售一段时间后，部分销售量y（斤）与销售单价x（元/斤）的数据统计如下表：

销售单价x（元/斤）

40

60

80

100

120

销售量y（斤）

160

120

80

40

0

(1)、根据图象求y与x的函数关系式；

(2)、商店想使销售利润不低于2400元，销售单价应定为多少？

(3)、为响应党中央“全面建成小康社会，实现共同富裕”的伟大号召，商店决定每销售一斤该茶叶，返给茶农a（a≤5）元钱，并保证在不低于82元的售价前提下，利润随售价的提高而增大，求a的取值范围.

查看试题解析
24. 已知正 $△$ ABC与正 $△$ CDE，连接BD，AE.

(1)、如图1，D点在BC上，点E在AC上，AE与BD的数量关系为；直线AE与直线BD所夹锐角为度；

(2)、将 $△$ CDE绕点C顺时针旋转至如图2，（1）中结论是否仍然成立？请说明理由；

(3)、若AB＝7，CD＝3，将 $△$ CDE绕点C顺时针旋转至B，D，E三点共线时，请画出图形，并求出BD长.

查看试题解析
25. 如图1，已知抛物线C₁：y＝ $\frac{1}{2}$ x²﹣2x+ $\frac{3}{2}$ 交x轴于点A，B，交y轴于点C.

(1)、直接写出点A，B，C的坐标；

(2)、在抛物线C₁上存在点D，使tan∠CBD＝ $\frac{1}{2}$ ，求点D的坐标；

(3)、将抛物线C₁向上平移至C₂ ， C₂的顶点P落在x轴上（如图2），M是C₂上的一个动点，连接PM，过点P作PN⊥PM，交C₂于点N，试问直线MN是否经过某定点？若必过某定点，请求出该定点的坐标；若不一定经过某定点，请说明理由.

查看试题解析

次数	第1次	第2次	第3次	第4次	第5次	第6次	第7次	第8次	第9次	第10次
号码	1	3	4	4	2	1	4	1

销售单价x（元/斤）	40	60	80	100	120
销售量y（斤）	160	120	80	40	0