江苏省淮安市2021年中考数学仿真模拟试卷
试卷更新日期:2021-05-31 类型:中考模拟
一、选择题
-
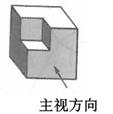
1. 如果a与3互为相反数,则 是( )A、3 B、﹣3 C、 D、﹣2. 下列各运算中,计算正确的是( )A、x3+2x3=3x6 B、(x3)3=x6 C、x3·x9=x12 D、x3÷x =x43. 如图所示的几何体的左视图是( )
 A、
A、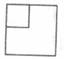 B、
B、 C、
C、 D、
D、 4. 一个多边形外角和是内角和的2倍,这个多边形是( )A、三角形 B、四边形 C、六边形 D、不能确定5. 点A(3,﹣1)关于原点的对称点A′的坐标是( )A、(﹣3,﹣1) B、(3,1) C、(﹣3,1) D、(﹣1,3)6. 2015年某中学举行的春季田径运动会上,参加男子跳高的15名运动员的成绩如表所示:
4. 一个多边形外角和是内角和的2倍,这个多边形是( )A、三角形 B、四边形 C、六边形 D、不能确定5. 点A(3,﹣1)关于原点的对称点A′的坐标是( )A、(﹣3,﹣1) B、(3,1) C、(﹣3,1) D、(﹣1,3)6. 2015年某中学举行的春季田径运动会上,参加男子跳高的15名运动员的成绩如表所示:成绩(m)
1.80
1.50
1.60
1.65
1.70
1.75
人数
1
2
4
3
3
2
这些运动员跳高成绩的中位数和众数分别是( )
A、1.70m,1.65m B、1.70m,1.70m C、1.65m,1.60m D、3,47. 如图, 均 为直径,点 是圆上两点,且 ,则 的度数是( )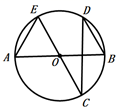 A、 B、 C、 D、8. 计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
A、 B、 C、 D、8. 计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:十六进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
十进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例如,十进制中 ,用十六进制表示为1A:用十六进制表示: , ,则 ,用 十六进制可表示为( )
A、8C B、140 C、32 D、EO二、填空题
-
9. 分解因式:4m2﹣9n2= .10. 第五届“中国数字阅读大会”在杭州举办,大会发布的《2018中国数字阅读白皮书》显示:截止2018年,我国数字阅读用户总量达到43200万人,将数据43200用科学记数法表示为 .11. 数据1,2,3,a的平均数是3,数据4,5,a,b的众数是5,则a+b= .12. 分式方程 的解为 .13. 如图,在菱形ABCD中,AC与BD相交于O,P是AB上一点,PO=PA=3,则菱形ABCD的周长是 .
 14. 菱形周长为40 cm,它的一条对角线长12 cm,则菱形的面积为cm215. 顶点为P的抛物线 与y轴交于Q , 则PQ的长为 .16. 如图,已知菱形 的对角线相交于坐标原点O,四个顶点分别在双曲线 和 上, .平行于x轴的直线与两双曲线分别交于点E,F,连接 , ,则 的面积为.
14. 菱形周长为40 cm,它的一条对角线长12 cm,则菱形的面积为cm215. 顶点为P的抛物线 与y轴交于Q , 则PQ的长为 .16. 如图,已知菱形 的对角线相交于坐标原点O,四个顶点分别在双曲线 和 上, .平行于x轴的直线与两双曲线分别交于点E,F,连接 , ,则 的面积为.
三、解答题
-
17.(1)、计算(2)、化简:18. 阅读下面的材料:
对于实数 ,我们定义符号 的意义为:当 时, ;当 时, ,如: .
根据上面的材料回答下列问题:
(1)、 ;(2)、当 时,求x的取值范围.19.某校九(2)班40名同学为“希望工程”捐款,共捐款400元,捐款情况如下表:表格中捐款10元和15元的人数不小心被墨水污染已看不清楚.捐款10元和15元的人数各是多少名?
捐款(元)
5
10
15
20
人数
12

3
20. 如图1,在▱ABCD中,对角线AC与BD相交于点O,经过点O的直线与边AB相交于点E,与边CD相交于点F.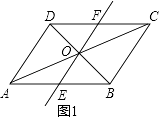 (1)、求证:OE=OF;(2)、如图2,连接DE,BF,当DE⊥AB时,在不添加其他辅助线的情况下,直接写出腰长等于 BD的所有的等腰三角形.
(1)、求证:OE=OF;(2)、如图2,连接DE,BF,当DE⊥AB时,在不添加其他辅助线的情况下,直接写出腰长等于 BD的所有的等腰三角形. 21. 为了调查疫情对青少年人生观、价值观产生的影响,轩宁中学团委对部分学生进行了问卷调查,其中一项是:疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两个统计图(不完整)如图所示,请你根据图中提供的信息回答下列问题:
21. 为了调查疫情对青少年人生观、价值观产生的影响,轩宁中学团委对部分学生进行了问卷调查,其中一项是:疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两个统计图(不完整)如图所示,请你根据图中提供的信息回答下列问题: (1)、本次调查共抽取了多少名学生?(2)、通过计算补全条形统计图;(3)、若轩宁中学共有 名学生,请你估计该中学选择“生命”词汇的学生有多少名?22. 现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)、本次调查共抽取了多少名学生?(2)、通过计算补全条形统计图;(3)、若轩宁中学共有 名学生,请你估计该中学选择“生命”词汇的学生有多少名?22. 现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾. (1)、写出小明投放的垃圾恰好是“厨余垃圾”的概率;(2)、用列表法或画树状图法求小丽投放的两袋垃圾是不同类的概率23.
(1)、写出小明投放的垃圾恰好是“厨余垃圾”的概率;(2)、用列表法或画树状图法求小丽投放的两袋垃圾是不同类的概率23.“低碳环保,你我同行”.两年来,绍兴市区的公共自行车给市民出行带来切实方便.如图1所示是一辆自行车的实物图.车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2,图3是公共自行车车桩的截面示意图,PQ⊥PM,PM⊥MN,点Q,N在GO上,GO∥HF,PQ=80cm,PM=24cm,QN=25cm,GH=4cm.
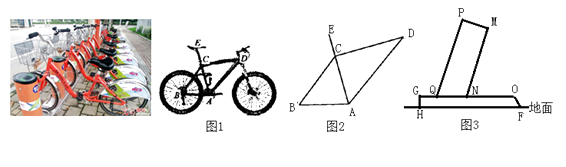 (1)、求车架档AD的长;(2)、求车座点E到车架档AB的距离及车桩的截面示意图中的点P到地面的距离.
(1)、求车架档AD的长;(2)、求车座点E到车架档AB的距离及车桩的截面示意图中的点P到地面的距离.(结果精确到1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75≈3.73)
24. 如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.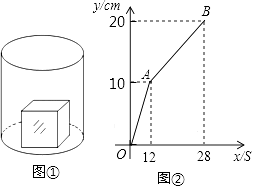 (1)、正方体的棱长为cm;(2)、求线段AB对应的函数解析式,并写出自变量x的取值范围;(3)、如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.25. 如图,△ABC内接于⊙O,且∠B=60°,过C作⊙O的切线l,与直径AD的延长线交于点E,AF⊥l,垂足为F.
(1)、正方体的棱长为cm;(2)、求线段AB对应的函数解析式,并写出自变量x的取值范围;(3)、如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.25. 如图,△ABC内接于⊙O,且∠B=60°,过C作⊙O的切线l,与直径AD的延长线交于点E,AF⊥l,垂足为F.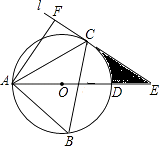 (1)、求证:AC平分∠FAD;(2)、已知AF=3 ,求阴影部分面积.26.(1)、问题发现
(1)、求证:AC平分∠FAD;(2)、已知AF=3 ,求阴影部分面积.26.(1)、问题发现
如图1,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=50°,连接BD,CE交于点F.填空:
①的值为;②∠BFC的度数为.
(2)、类比探究如图2,在矩形ABCD和△DEF中,AD= AB,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点P.求 的值及∠APC的度数,并说明理由;
(3)、拓展延伸在(2)的条件下,将△DEF绕点D在平面内旋装,AF,CE所在直线交于点P,若DF= ,AB= ,求出当点P与点E重合时AF的长.
27. 如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C . 直线y=x﹣5经过点B、C .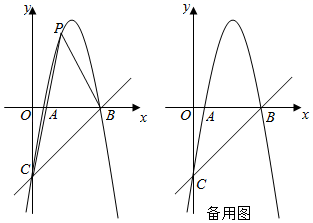 (1)、求抛物线的解析;(2)、点P是直线BC上方抛物线上一动点,连接PB、PC .
(1)、求抛物线的解析;(2)、点P是直线BC上方抛物线上一动点,连接PB、PC .①当△PBC的面积最大时,求点P的坐标;
②在①的条件下,y轴上存在点M , 使四边形PMAB的周长最小,请求出点M的坐标;
③连接AC , 当tan∠PBO=2tan∠ACO时,请直接写出点P的坐标.