江苏省盐城市2021年中考数学仿真模拟试卷
试卷更新日期:2021-05-31 类型:中考模拟
一、选择题
-
1. 2020的相反数是( )A、 2020 B、﹣2020 C、 D、2. 下列图形中,是中心对称但不是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、﹣a4b÷a2b=﹣a2b B、(a﹣b)2=a2﹣b2 C、a2•a3=a6 D、﹣3a2+2a2=﹣a24. 实数a、b在数轴上的对应点的位置如图所示,则正确的结论是( )
3. 下列计算正确的是( )A、﹣a4b÷a2b=﹣a2b B、(a﹣b)2=a2﹣b2 C、a2•a3=a6 D、﹣3a2+2a2=﹣a24. 实数a、b在数轴上的对应点的位置如图所示,则正确的结论是( ) A、a<﹣1 B、ab>0 C、a﹣b<0 D、a+b<05.
A、a<﹣1 B、ab>0 C、a﹣b<0 D、a+b<05.如图所示,两个紧靠在一起的圆柱体组成的物体,它的主视图是( )
 A、
A、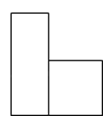 B、
B、 C、
C、 D、
D、 6. 今年我市参加中考的人数大约有41300人,将41300用科学记数法表示为( )A、413×102 B、41.3×103 C、4.13×104 D、0.413×1037. 周末回家,妈妈买了苹果、梨、柚子、橘子四种水果共50个,如果把苹果的个数加4,梨的个数减4,柚子的个数乘4,橘子的个数除以4,最后四种水果的个数相等,那么橘子的个数是( )
6. 今年我市参加中考的人数大约有41300人,将41300用科学记数法表示为( )A、413×102 B、41.3×103 C、4.13×104 D、0.413×1037. 周末回家,妈妈买了苹果、梨、柚子、橘子四种水果共50个,如果把苹果的个数加4,梨的个数减4,柚子的个数乘4,橘子的个数除以4,最后四种水果的个数相等,那么橘子的个数是( )
A、8个 B、12个 C、16个 D、32个8. 如图,在长方形ABCD中,AB=6,BC=8,∠ABC的平分线交AD于点E,连接CE,过B点作BF⊥CE于点F,则BF的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
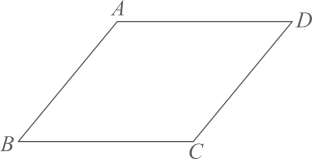
9. 如图,AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,则∠ADB度数为 .
 10. 为迎接五月份全县中考九年级体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
10. 为迎接五月份全县中考九年级体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据唯一众数是13,平均数是12,那么这组数据的方差是 .
11. 因式分解: .12. 分式方程 = 的解为.13. 为了对1000件某品牌衬衣进行抽检,统计合格衬衣的件数,在相同条件下,经过大量的重复抽检,发现一件合格衬衣的频率稳定在常数0.98附近,由此可估计这1000件中不合格的衬衣约为件.14. 如图,AC是⊙O的直径,∠ACB=60°,连接AB,过A、B两点分别作⊙O的切线,两切线交于点P.若已知⊙O的半径为1,则△PAB的周长为 .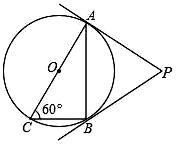 15. 边长为4的正方形ABCD,在BC边上取一动点E,连接AE,作EF⊥AE,交CD边于点F,若CF的长为 ,则CE的长为 .
15. 边长为4的正方形ABCD,在BC边上取一动点E,连接AE,作EF⊥AE,交CD边于点F,若CF的长为 ,则CE的长为 . 16. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上, ,顶点C的坐标为 ,x反比例函数 的图象与菱形对角线AO交于点D,连接BD,当 轴时,k的值是.
16. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上, ,顶点C的坐标为 ,x反比例函数 的图象与菱形对角线AO交于点D,连接BD,当 轴时,k的值是.
三、解答题
-
17. 计算:( ﹣1)0+(﹣3)2﹣2sin60°.18. 解不等式组 ,并写出它的所有整数解.19. 先化简,再求值: ÷(1﹣ ),其中a= ﹣2.20. 如图,在△ABC中,AD是BC边上的高,tan C= , AC=3,AB=4,求BD的长.(结果保留根号)

21. 如图,在 中, , , ,D、E分别是斜边AB、直角边BC上的点,把 沿着直线DE折叠. (1)、如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE; 不写作法和证明,保留作图痕迹(2)、如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长.22. 某厂为了解工人在单位时间内加工同一种零件的技能水平,随机抽取了50名工人加工的零件进行检测,统计出他们各自加工的合格品数是1到8这八个整数,现提供统计图的部分信息如图,
(1)、如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE; 不写作法和证明,保留作图痕迹(2)、如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长.22. 某厂为了解工人在单位时间内加工同一种零件的技能水平,随机抽取了50名工人加工的零件进行检测,统计出他们各自加工的合格品数是1到8这八个整数,现提供统计图的部分信息如图,
请解答下列问题:
(1)、根据统计图,求这50名工人加工出的合格品数的中位数.(2)、写出这50名工人加工出合格品数的众数的可能取值(3)、厂方认定,工人在单位时间内加工出的合格品数不低于3件为技能合格,否则,将接受技能再培训.已知该厂有同类工人400名,请估计该厂将接受技能再培训的人数.23. 动画片《小猪佩奇》分靡全球,受到孩子们的喜爱.现有4张《小猪佩奇》角色卡片,分别是A佩奇,B乔治,C佩奇妈妈,D佩奇爸爸(四张卡片除字母和内容外,其余完全相同).姐弟两人做游戏,他们将这四张卡片混在一起,背面朝上放好.
(1)、姐姐从中随机抽取一张卡片,恰好抽到A佩奇的概率为;
(2)、若两人分别随机抽取一张卡片(不放回),请用列表或画树状图的分方法求出恰好姐姐抽到A佩奇弟弟抽到B乔治的概率. 24. 如图,在四边形 中, ,过点B的 与边 分别交于E,F两点. ,垂足为G, .连接 .
24. 如图,在四边形 中, ,过点B的 与边 分别交于E,F两点. ,垂足为G, .连接 .
 (1)、若 ,试判断 的形状,并说明理由;(2)、若 ,求证: 与 相切于点A.25. 如图1,已知抛物线 过点 .
(1)、若 ,试判断 的形状,并说明理由;(2)、若 ,求证: 与 相切于点A.25. 如图1,已知抛物线 过点 . (1)、求抛物线的解析式及其顶点C的坐标;(2)、设点D是x轴上一点,当 时,求点D的坐标;(3)、如图2.抛物线与y轴交于点E,点P是该抛物线上位于第二象限的点,线段PA交BE于点M,交y轴于点N, 和 的面积分别为 ,求 的最大值.26. 勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1)后人称之为“赵爽弦图”,流传至今.(1)、①请叙述勾股定理;
(1)、求抛物线的解析式及其顶点C的坐标;(2)、设点D是x轴上一点,当 时,求点D的坐标;(3)、如图2.抛物线与y轴交于点E,点P是该抛物线上位于第二象限的点,线段PA交BE于点M,交y轴于点N, 和 的面积分别为 ,求 的最大值.26. 勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1)后人称之为“赵爽弦图”,流传至今.(1)、①请叙述勾股定理;②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)


 (2)、①如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足 的有个;
(2)、①如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足 的有个;
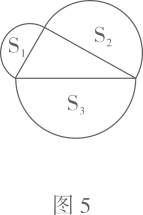

②如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为 , ,直角三角形面积为 ,请判断 , , 的关系并证明;
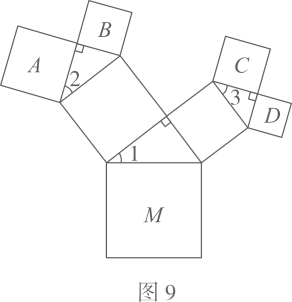
 (3)、如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图8所示的“勾股树”.在如图9所示的“勾股树”的某部分图形中,设大正方形 的边长为定值 ,四个小正方形A,B,C,D的边长分别为a,b,c,d,已知 ,则当 变化时,回答下列问题:(结果可用含 的式子表示)
(3)、如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图8所示的“勾股树”.在如图9所示的“勾股树”的某部分图形中,设大正方形 的边长为定值 ,四个小正方形A,B,C,D的边长分别为a,b,c,d,已知 ,则当 变化时,回答下列问题:(结果可用含 的式子表示)① ;
②b与c的关系为 , a与d的关系为.

 27. 二次函数y=a(x﹣h)2+k(a≠0)的图象是抛物线,定义一种变换,先作这条抛物线关于原点对称的抛物线y′,再将得到的对称抛物线y′向上平移m(m>0)个单位,得到新的抛物线ym , 我们称ym叫做二次函数y=a(x﹣h)2+k(a≠0)的m阶变换.(1)、已知:二次函数y=2(x+2)2+1,它的顶点关于原点的对称点为 , 这个抛物线的2阶变换的表达式为 .(2)、若二次函数M的6阶变换的关系式为y6′=(x﹣1)2+5.
27. 二次函数y=a(x﹣h)2+k(a≠0)的图象是抛物线,定义一种变换,先作这条抛物线关于原点对称的抛物线y′,再将得到的对称抛物线y′向上平移m(m>0)个单位,得到新的抛物线ym , 我们称ym叫做二次函数y=a(x﹣h)2+k(a≠0)的m阶变换.(1)、已知:二次函数y=2(x+2)2+1,它的顶点关于原点的对称点为 , 这个抛物线的2阶变换的表达式为 .(2)、若二次函数M的6阶变换的关系式为y6′=(x﹣1)2+5.①二次函数M的函数表达式为 .
②若二次函数M的顶点为点A , 与x轴相交的两个交点中左侧交点为点B , 在抛物线y6′=(x﹣1)2+5上是否存在点P , 使点P与直线AB的距离最短,若存在,求出此时点P的坐标.
(3)、抛物线y=﹣3x2﹣6x+1的顶点为点A , 与y轴交于点B , 该抛物线的m阶变换的顶点为点C.若△ABC是以AB为腰的等腰三角形,请直按写出m的值.