江苏省南通市2021年中考数学仿真模拟试卷

试卷更新日期：2021-05-31 类型：中考模拟

进入出卷网下载

一、选择题

1. $| - 5 + 3 |$ 计算的结果是（）

A、-2 B、2 C、-8 D、8

查看试题解析
2. 宁波栎社国际机场三期扩建工程建设总投资84.5亿元，其中84.5亿元用科学记数法表示为（）

A、0.845×10¹⁰元 B、84.5×10⁸元 C、8.45×10⁹元 D、8.45×10¹⁰元

查看试题解析
3. 下列计算正确的是（）

A、 $2 + \sqrt{3} = 2 \sqrt{3}$ B、 $a + a^{2} = a^{3}$ C、 $2 a \cdot 3 a = 6 a$ D、 $x^{6} \div x^{2} = x^{4}$

查看试题解析
4. 以原点为中心，将点 $P (3 ， 4)$ 按逆时针方向旋转 $90 °$ ，得到的点Q所在的象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 如图，已知∠1＝39°，∠2＝39°，∠3＝54°，则∠4的度数是（）

A、39° B、51° C、54° D、126°

查看试题解析
6. 为鼓励同学们阅读经典，了解同学们课外阅读经典名著的情况，在某年级随机抽查了20名同学每期的课外阅读名著的情况，调查结果如表：

课外名著阅读量（本）

8

9

10

11

12

学生数

3

3

4

6

4

则关于这20名周学课外阅读经典名著的情况，下列说法正确的是（）

A、中位数是10 B、平均数是10.25 C、众数是12 D、以上说法均不符合题意

查看试题解析
7. 下列说法错误的是（）

A、两组对边分别相等的四边形是平行四边形 B、对角线相等的平行四边形是矩形 C、一个角是直角的平行四边形是正方形 D、对角线互相平分且垂直的四边形是菱形

查看试题解析
8. 如图，是某几何体的三视图及相关数据，则该几何体的侧面积是（）

A、10π B、15π C、20π D、30π

查看试题解析
9. 如图1，在矩形ABCD中，动点E从A出发，沿 $A - B - C$ 方向运动，当点E到达点C时停止运动，过点E做 $F E ⊥ A E$ ，交CD于F点，设点E运动路程为x， $F C = y$ ，如图2所表示的是y与x的函数关系的大致图象，当点E在BC上运动时，FC的最大长度是 $\frac{2}{5}$ ，则矩形ABCD的面积是（）

A、 $\frac{23}{5}$ B、 $\frac{25}{4}$ C、6 D、5

查看试题解析
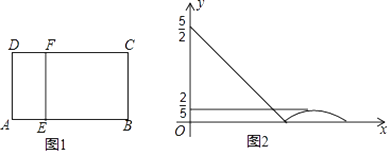10. 如图所示，点P是边长为2的正方形ABCD的对角线BD上的动点，过点P分别作PE⊥BC于点E，PF⊥DC于点F，连接AP并延长，交射线BC于点H，交射线DC于点M，连接EF交AH于点G，当点P在BD上运动时（不包括B、D两点），以下结论中：①MF＝MC；②AP＝EF；③AH⊥EF；④AP²＝PM•PH；⑤EF的最小值是 $\sqrt{2}$ ．其中正确结论有（）

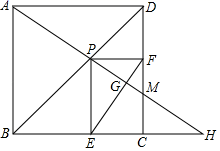A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

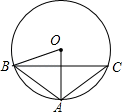
11. 分解因式：x²-4x=。

查看试题解析
12. 如图，⊙O是△ABC的外接圆，∠AOB＝60°，AB＝AC＝2，则弦BC＝．

查看试题解析
13. 满足 $\sqrt{5} < x < \sqrt{18}$ 的整数x的值是.

查看试题解析
14. 如图，在 $▱ A B C D$ 中，点 $E$ 在 $B C$ 上， $A E$ 与 $B D$ 相交于点 $F$ ，若 $\frac{B E}{E C} = \frac{4}{5}$ ，则 $\frac{B F}{F D} =$ .

查看试题解析
15. 某学校生物兴趣小组在该校空地上围了一块面积为200m²的矩形试验田，用来种植蔬菜.如图，试验田一面靠墙，墙长35m，另外三面用49m长的篱围成，其中一边开有一扇1m宽的门（不包括篱笆）.设试验田垂直于墙的一边AB的长为xm，则所列方程为.

查看试题解析
16.
如图，为测量某栋楼房AB的高度，在C点测得A点的仰角为30°，朝楼房AB方向前进10米到达点D，再次测得A点的仰角为60°，则此楼房的高度为米（结果保留根号）．

查看试题解析
17. 已知实数m，n满足3m²+6m﹣5=0，3n²+6n﹣5=0，且m≠n，则 $\frac{n}{m} + \frac{m}{n}$ = ．

查看试题解析
18. 如图，直线 $A B$ 与双曲线 $y = \frac{k}{x} (k > 0)$ 在第一象限内交于A、B两点，与x轴交于点C，点B为线段 $A C$ 的中点，连接 $O A$ ，若 $△ A O C$ 的面积为3，则k的值为.

查看试题解析

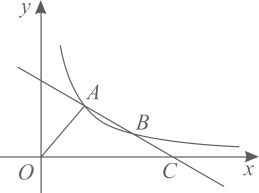
三、解答题

19. 计算：

(1)、（x+y）²+y（3x﹣y）；

(2)、（ $\frac{4 - a^{2}}{a - 1}$ +a）÷ $\frac{a^{2} - 16}{a - 1}$ .

查看试题解析
20. 如图，在矩形ABCD中，点F在边BC上，且AF=AD，过点D作DE⊥AF，垂足为点E．

(1)、求证：DE=AB．

(2)、以D为圆心，DE为半径作圆弧交AD于点G．若BF=FC=1，试求 $\hat{E G}$ 的长．

查看试题解析
21. 如图，直线 $l_{1} ： y = 2 x + 1$ 与 $x$ 轴、 $y$ 轴交于点 $D$ 、 $A$ ，直线 $l_{2} ： y = m x + 4$ 与 $x$ 轴 $y$ 轴分别交于点 $C$ 、 $B$ ，两直线相交于点 $P (1 ， b)$ ．

(1)、求 $b$ ， $m$ 的值；

(2)、求 $S_{△ P D C} - S_{△ P A B}$ 的值；

(3)、垂直于 $x$ 轴的直线 $x = a$ 与直线 $l_{1}$ ， $l_{2}$ 分别交于点 $M$ ， $N$ ，若线段 $M N$ 的长为2，求 $a$ 的值．

查看试题解析
22. 一次学科测验，学生得分均为整数，满分10分，成绩达到6分以上为合格．成绩达到9分为优秀．这次测验中甲乙两组学生成绩分布的条形统计图如下：

(1)、请补充完成下面的成绩统计分析表：

(2)、甲组学生说他们的合格率、优秀率均高于乙组，所以他们的成绩好于乙组．但乙组学生不同意甲组学生的说法，认为他们组的成绩要高于甲组．请你给出三条支持乙组学生观点的理由．

查看试题解析
23. 宜昌景色宜人，其中三峡大坝、清江画廊、三峡人家景点的景色更是美不胜收.某民营单位为兼顾生产和业余生活，决定在下设的A，B，C三部门利用转盘游戏确定参观的景点，两转盘各部分圆心角大小以及选派部门、旅游景点等信息如图.

(1)、若规定老同志相对偏多的部门选中的可能性大，试判断这个部门是哪个部门？请说明理由；

(2)、设选中C部门游三峡大坝的概率为 $P_{1}$ ，选中B部门游清江画廊或者三峡人家的概率为 $P_{2}$ ，请判断 $P_{1}$ ， $P_{2}$ 大小关系，并说明理由.

查看试题解析
24. 如图，在正方形ABCD中，点E在BC边上，连接AE ， ∠DAE的平分线AG与CD边交于点G ，与BC的延长线交于点F ．设 $\frac{C E}{E B}$ ＝λ（λ＞0）．

(1)、若AB＝2，λ＝1，求线段CF的长．

(2)、连接EG ，若EG⊥AF ，
①求证：点G为CD边的中点．

②求λ的值．

查看试题解析
25. 已知y关于x的二次函数y=x²-bx+ $\frac{1}{4}$ b²+b-5的图象与x轴有两个公共点.

(1)、求b的取值范围；

(2)、若b取满足条件的最大整数值，当m≤x≤ $\frac{3}{2}$ 时，函数y的取值范围是n≤y≤6-2m，求m，n的值；

(3)、若在自变量x的值满足b≤x≤b+3的情况下，对应函数y的最小值为 $\frac{1}{4}$ ，求此时二次函数的解析式.

查看试题解析
26. 问题背景：如图①，在四边形ADBC中，∠ACB＝∠ADB＝90°，AD＝BD，探究线段AC、BC、CD之间的数量关系.
小吴同学探究此问题的思路是：将ΔBCD绕点D逆时针旋转90°到ΔAED处，点B、C分别落在点A、E处（如图②），易证点C、A、E在同一条直线上，并且ΔCDE是等腰直角三角形，所以CE＝ $\sqrt{2}$ CD，从而得出结论：AC+BC＝ $\sqrt{2}$ CD．

图①

图②

图③

图④

简单应用：

(1)、在图①中，若AC＝ $\sqrt{2}$ ，BC＝2 $\sqrt{2}$ ，则CD＝.

(2)、如图③，AB是⊙O的直径，点C、D在⊙O上，弧AD＝弧BD，若AB＝13，BC＝12，求CD的长.

(3)、拓展延伸：
如图④，∠ACB＝∠ADB＝90°，AD＝BD，若AC＝m，BC＝n（m<n），求CD的长（用含m，n的代数式表示）.

查看试题解析

课外名著阅读量（本）	8	9	10	11	12
学生数	3	3	4	6	4