辽宁省沈阳市皇姑区2021年中考数学一模试卷
试卷更新日期:2021-05-28 类型:中考模拟
一、单选题
-
1. 下列算式中,计算结果是负数的是A、 B、 C、 D、2. 据有关部门初步统计,自新冠肺炎疫情发生以来,国家已经投入1390亿资金进行疫情防控,为抗击疫情提供了强力保障,也展现了祖国日益强大的综合国力!将数据1390亿用科学记数法表示为1.390×10n , 其中n的值为( )A、4 B、10 C、11 D、33. 如图是一个三视图,则此三视图所对应的直观图是( )
 A、
A、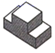 B、
B、 C、
C、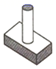 D、
D、 4. 化简 的结果正确的是( )A、395 B、 C、3 D、4035. 在一个不透明的袋子里装有红球,黄球共60个,这些球除颜色外其他都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )A、9 B、15 C、18 D、246. 5名同学的身高分别为165,172,168,170,175(单位:厘米).增加1名身高为 的同学后,现在6名同学的身高的平均数与方差与原来相比( )A、平均数不变,方差变小 B、平均数变大,方差不变 C、平均数不变,方差变大 D、平均数变小,方差不变7. 如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )
4. 化简 的结果正确的是( )A、395 B、 C、3 D、4035. 在一个不透明的袋子里装有红球,黄球共60个,这些球除颜色外其他都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )A、9 B、15 C、18 D、246. 5名同学的身高分别为165,172,168,170,175(单位:厘米).增加1名身高为 的同学后,现在6名同学的身高的平均数与方差与原来相比( )A、平均数不变,方差变小 B、平均数变大,方差不变 C、平均数不变,方差变大 D、平均数变小,方差不变7. 如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )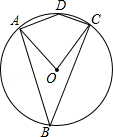 A、80° B、100° C、60° D、40°8. 如图,A,B两景点相距20km,C景点位于A景点北偏东60°方向上,位于B景点北偏西30°方向上,则A,C两景点相距( )
A、80° B、100° C、60° D、40°8. 如图,A,B两景点相距20km,C景点位于A景点北偏东60°方向上,位于B景点北偏西30°方向上,则A,C两景点相距( )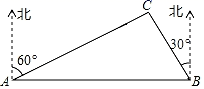 A、10km B、10 km C、10 km D、 km9. 某公司2020年3月份营业额为60万元,5月份营业额达到100万元,设该公司这两个月的月平均增长率为x.应列方程是( )A、60(1+x)=100 B、60(1+x)2=100 C、60(1+x)+60(1+x)2=100 D、60+60(1+x)+60(1+x)2=10010. 如图是二次函数 图象的一部分,对称轴为 ,且经过点 .下列说法:① ;② ;③ ;④若 , 是抛物线上的两点,则 .其中说法正确的是( )
A、10km B、10 km C、10 km D、 km9. 某公司2020年3月份营业额为60万元,5月份营业额达到100万元,设该公司这两个月的月平均增长率为x.应列方程是( )A、60(1+x)=100 B、60(1+x)2=100 C、60(1+x)+60(1+x)2=100 D、60+60(1+x)+60(1+x)2=10010. 如图是二次函数 图象的一部分,对称轴为 ,且经过点 .下列说法:① ;② ;③ ;④若 , 是抛物线上的两点,则 .其中说法正确的是( ) A、①②③ B、②③④ C、①③④ D、①②④
A、①②③ B、②③④ C、①③④ D、①②④二、填空题
-
11. 因式分解: .12. 不等式 的解集是 .13. 若一个多边形的每一个外角都为 则该多边形为边形.14. 如图,AB//CD,∠D=60°,FB=FE,则∠E=°.
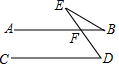 15. 如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1﹣k2=.
15. 如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1﹣k2=.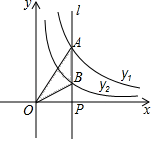 16. 如图,在平行四边形 中, , , ,P是平行四边形 边上一动点,连接 ,若 是直角三角形,则线段 的长为 .
16. 如图,在平行四边形 中, , , ,P是平行四边形 边上一动点,连接 ,若 是直角三角形,则线段 的长为 .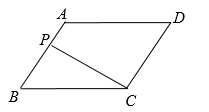
三、解答题
-
17. 计算: .18. 在四编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中机抽取一张.
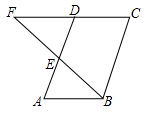
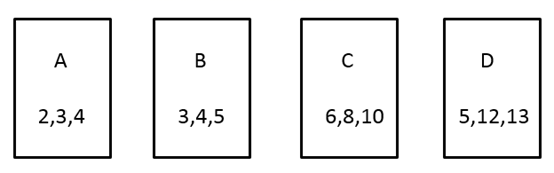 我们知道,满足 的三个正整数a,b,c成为勾股数,请用“列表法”或“树状图法”求抽到的两张卡片上的数都是勾股数的概率(卡片用A,B,C,D表示).19. 如图,在 中,E是边 的中点, 的延长线与 的延长线相交于点F.
我们知道,满足 的三个正整数a,b,c成为勾股数,请用“列表法”或“树状图法”求抽到的两张卡片上的数都是勾股数的概率(卡片用A,B,C,D表示).19. 如图,在 中,E是边 的中点, 的延长线与 的延长线相交于点F.求证: .
 20. 某校为了解九年级学生的疫情防控识情况,在全校九年级随机抽部分学生进行问卷调查.根据调查结果,把学生的防控意识分成“A.很强”、“B.较强”、“C.一般”、“D.淡薄”四个层次,将调查的结果绘制如图两幅不完整的统计图,请根据图中的信息,解答下列问题:
20. 某校为了解九年级学生的疫情防控识情况,在全校九年级随机抽部分学生进行问卷调查.根据调查结果,把学生的防控意识分成“A.很强”、“B.较强”、“C.一般”、“D.淡薄”四个层次,将调查的结果绘制如图两幅不完整的统计图,请根据图中的信息,解答下列问题: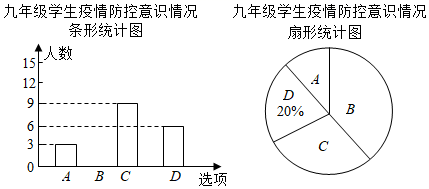 (1)、求本次共调查了多少名学生?(2)、直接在图中将条形统计图补充完整;(3)、如果把疫情防控意识“很强或较强”视为合格,该校九年级共有1200名学生,请你估计合格的学生有多少名?21. 某地有甲、乙两家口罩厂,已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且乙厂单独完成48万只口罩的生产比甲厂单独完成48万只口罩的生产多用4天.(1)、求甲、乙厂每天分别可以生产多少万只口罩?(2)、该地委托甲、乙两厂尽快完成100万只口罩的生产任务,问两厂同时生产至少需要多少天才能完成生产任务?22. 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)、求本次共调查了多少名学生?(2)、直接在图中将条形统计图补充完整;(3)、如果把疫情防控意识“很强或较强”视为合格,该校九年级共有1200名学生,请你估计合格的学生有多少名?21. 某地有甲、乙两家口罩厂,已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且乙厂单独完成48万只口罩的生产比甲厂单独完成48万只口罩的生产多用4天.(1)、求甲、乙厂每天分别可以生产多少万只口罩?(2)、该地委托甲、乙两厂尽快完成100万只口罩的生产任务,问两厂同时生产至少需要多少天才能完成生产任务?22. 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.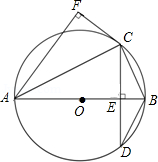 (1)、求证:CF是⊙O的切线;(2)、若sin∠BAC= ,求 的值.23. 如图,在平面直角坐标系中,直线 与y轴交于点A,与x轴交于点B,动点G从点A出发沿线段 向点B运动,速度为每秒 个单位长度,设运动时间为 秒.过点A作 (点F在第一象限),连接 并延长交 于点E.
(1)、求证:CF是⊙O的切线;(2)、若sin∠BAC= ,求 的值.23. 如图,在平面直角坐标系中,直线 与y轴交于点A,与x轴交于点B,动点G从点A出发沿线段 向点B运动,速度为每秒 个单位长度,设运动时间为 秒.过点A作 (点F在第一象限),连接 并延长交 于点E.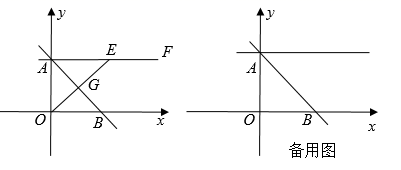 (1)、当 , 时;
(1)、当 , 时;①求线段 的长;
②求证: ;
③直接写出直线 的表达式;
(2)、当 , 时,射线 与射线 相交于点M,且 ,直接写出b的值.24. 已知,矩形 中, , ,点E是射线 上一动点,将矩形 沿直线 翻折,点B落在点F处,展开后再将矩形 沿直线 翻折,点E落在点G处,再将图形展开,连接 、 、 ,得到四边形 .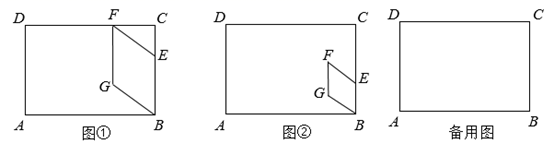 (1)、如图①,若点F恰好落在 边上,求线段 的长;(2)、如图②,若 ,直接写出点F到 边的距离;(3)、若 的面积为3,直接写出四边形 的面积.25. 如图,在平面直角坐标系中,抛物线 交y轴于点A,交x轴于点 和点 ,点Q在第一象限的抛物线上,连接 、 、 , 与y轴交于点N.
(1)、如图①,若点F恰好落在 边上,求线段 的长;(2)、如图②,若 ,直接写出点F到 边的距离;(3)、若 的面积为3,直接写出四边形 的面积.25. 如图,在平面直角坐标系中,抛物线 交y轴于点A,交x轴于点 和点 ,点Q在第一象限的抛物线上,连接 、 、 , 与y轴交于点N.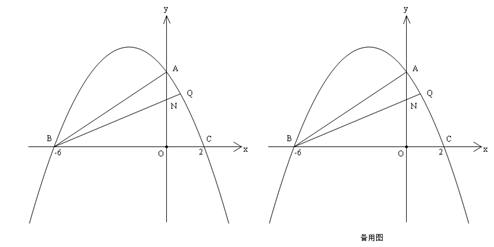 (1)、求抛物线表达式;(2)、当 的面积等于7时,设点Q的横坐标为m,求m的值;(3)、在(2)的条件下,点M在x轴上,点E在平面内,若 ,且四边形 是平行四边形.
(1)、求抛物线表达式;(2)、当 的面积等于7时,设点Q的横坐标为m,求m的值;(3)、在(2)的条件下,点M在x轴上,点E在平面内,若 ,且四边形 是平行四边形.①直接写出点E的坐标;
②设射线 与 相交于点P,交 于点H,将 绕点B旋转一周,旋转后的三角形记为 ,直接写出 的最小值.