吉林省吉林市船营区2021年中考数学一模试卷

试卷更新日期：2021-05-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 2021的倒数是（）

A、 $- 2021$ B、 $- \frac{1}{2021}$ C、2021 D、 $\frac{1}{2021}$

查看试题解析
2. 柜子里有5双鞋，取出一只鞋是右脚鞋的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{5}$ D、 $\frac{1}{10}$

查看试题解析
3. 如图，是一个几何体的表面展开图，则该几何体是（）

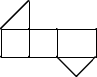A、正方体 B、长方体 C、三棱柱 D、四棱锥

查看试题解析
4. 如图，赵师傅透过平举的放大镜从正上方看水平桌面上的菱形图案的一角，那么∠A与放大镜中的∠C的大小关系是（）

A、∠A＝∠C B、∠A>∠C C、∠A<∠C D、无法比较

查看试题解析
5. 二次函数y＝ax²＋bx＋c的自变量x与函数y的对应值如下表：
x
…
－5
－4
－3
－2
－1
0
…
y
…
4
0
－2
－2
0
4
…
下列说法正确的是（）

A、抛物线的开口向下 B、当x＞－3时，y随x的增大而增大 C、二次函数的最小值是－2 D、抛物线的对称轴是直线x＝－ $\frac{5}{2}$

查看试题解析
6. 图1是一个地铁站入口的双翼闸机.如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC＝BD＝54cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30°.当双翼收起时，可以通过闸机的物体的最大宽度为（）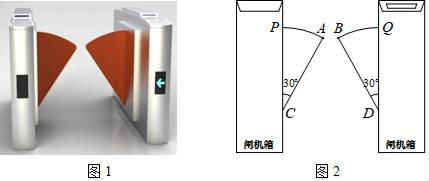

A、(54 $\sqrt{3}$ +10) cm B、(54 $\sqrt{2}$ +10) cm C、64 cm D、54cm

查看试题解析

二、填空题

7. 分解因式： $8 a^{2} - 2 a =$ ．

查看试题解析
8. 若关于x的方程kx²+2x﹣1=0有实数根，则k的取值范围是.

查看试题解析
9. 《九章算术》中记载一问题如下：“今有共买物，人出八，盈三：人出七，不足四，问人数、物价各几何？”意思是：今有人合伙购物，每人出 $8$ 钱，会多 $3$ 钱；每人出 $7$ 钱，又差 $4$ 钱，问人数、物价各多少？设有 $x$ 人，依题意列方程得．

查看试题解析
10. 如图，在 $△ A B C$ 中， $A C = B C ， ∠ B = 65 °$ ，分别以点A、C为圆心，大于 $\frac{1}{2} A C$ 的长为半径作弧，两弧相交于两点，过这两点作直线 $D E$ ，分别交 $A C$ 、 $B C$ 于点D、E ，连接 $A E$ ，则 $∠ A E D$ 的度数为度．

查看试题解析
11. 如图，点A在双曲线 $y = \frac{k}{x} (k > 0)$ 上，点B在双曲线 $y = \frac{1}{x}$ 上，且 $A B / / x$ 轴，点C和点D在x轴上．若四边形 $A B C D$ 为矩形，且矩形 $A B C D$ 的面积为2，则k的值为．

查看试题解析
12. 如图，AB为半圆O的直径，现将一块等腰直角三角板如图放置，锐角顶点P在半圆上，斜边过点B，一条直角边交该半圆于点Q．若AB＝2，则线段BQ的长为.

查看试题解析
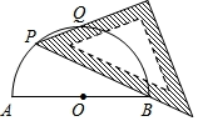13. 如图， $▱$ ABCD的顶点B在矩形AEFC的边EF上，点B与点E、F不重合．若△ACD的面积为3，则图中的阴影部分两个三角形的面积和为

查看试题解析
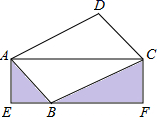14. 如图，在平面直角坐标系中，点P为抛物线y＝x²﹣ $\frac{1}{2}$ ax+a的顶点，点A、B在x轴上且AB＝2，当点P在x轴上方且△PAB面积最大时，a的值为．

查看试题解析

三、解答题

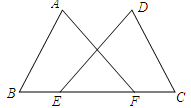
15. 先化简，再求值： ${(a - b)}^{2} - (a + b) (a - b)$ ，其中 $a = - 3, b = 2$ ．

查看试题解析
16. 甲、乙两人都握有分别标记为A、B、C的三张牌，两人做游戏，游戏规则是：每人各出一张牌，若两人出的牌相同，则为平局．用树状图或列表等方法，列出甲、乙两人一次游戏的所有可能的结果，并求出平局的概率．

查看试题解析
17. 如图，点E、F在BC上，BE＝CF，AB＝DC，∠B＝∠C．求证：∠A＝∠D．

查看试题解析
18. 某小区为了铺设一段全长为480米的道路，为减少施工对居民生活的影响，需缩短施工时间，实际施工时每天的工作效率比原计划提高20%，结果提前2天完成任务。求原计划每天铺设多少米？

查看试题解析
19. 如图，是 $6 \times 6$ 的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1，线段 $A B$ 的两个端点均在小正方形的格点上．

(1)、如图①，点P在小正方形的格点上，则 $\sin ∠ P A B =$ ．

(2)、在图①中画出以线段 $P A$ 为边的格点正方形．

(3)、在图②，图③中分别画出以线段 $A B$ 为边和对角线的矩形（面积不为8），且另外两个顶点C、D均在小正方形的格点上．分别写出你所画出矩形的面积．

查看试题解析
20. 钓鱼岛历来就是我们中国的固有领土，是神圣不可侵犯的！如图是钓鱼岛中某个岛礁上的斜坡 $A C$ ，我海监船在海面上与点C距离200米的D处，测得岛礁顶端A的仰角为 $26.6 °$ ，以及该斜坡坡度是 $\tan α = \frac{3}{4}$ ，求该岛礁的高 $A B$ （结果取整数）．（参考数据： $\sin 26.6 ° \approx 0.45 ， \cos 26.6 ° \approx 0.89 ， \tan 26.6 ° \approx 0.50$ ）

查看试题解析
21. 如图，BE是圆O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C，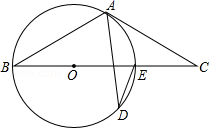

(1)、若∠ADE=25°，求∠C的度数；

(2)、若AB=AC，CE=2，求⊙O半径的长.

查看试题解析

22. 在建设港珠澳大桥期间，大桥的规划选线须经过中华白海豚国家级自然保护区---区域A或区域B ．为实现白海豚“零伤亡，不搬家”的目标，需合理安排施工时间和地点，为此，海豚观察员在相同条件下连续出海20天，在区域A ， B两地对中华白海豚的踪迹进行了观测和统计，过程如下，请补充完整．（单位：头）

（收集数据）

连续20天观察不同中华白海豚每天在区域A ，区域B出现的数目情况，得到统计结果，并按从小到大的顺序排列如下：

区域A 0 1 3 4 5 6 6 6 7 8 8 9 11 14 15 15 17 23 25 30

B 1 1 3 4 6 6 8 9 11 12 14 15 16 16 16 17 22 25 26 35

(1)、（整理、描述数据）

按如下数段整理、描述这两组数据，请补充完整：

海豚数x	0≤x≤7	8≤x≤14	15≤x≤21	22≤x≤28	29≤x≤35
区域A	9	5	3
区域B	6	5	5	3	1

(2)、两组数据的极差、平均数、中位数，众数如下表所示

观测点	极差	平均数	中位数	众数
区域A	a	10.65	b	c
区域B	34	13.15	13	16

请填空：上表中，极差a= ，中位数b= ，众数c=；

(3)、规划者们选择了区域A为大桥的必经地，为减少施工对白海豚的影响，合理安排施工时间，估计在接下来的200天施工期内，区域A大约有多少天中华白海豚出现的数目在22≤x≤35的范围内？

查看试题解析

23. 某校初三年级进行女子800米测试，甲、乙两名同学同时起跑，甲同学先以a米/秒的速度匀速跑，一段时间后提高速度，以 $\frac{5}{3} a$ 米/秒的速度匀速跑，b秒到达终点，乙同学在第60秒和第140秒时分别减慢了速度，设甲、乙两名同学所的路程为s（米），乙同学所用的时间为t（秒），s与t之间的函数图象如图所示.

(1)、乙同学起跑的速度为米/秒；

(2)、求a、b的值；

(3)、当乙同学领先甲同学60米时，直接写出t的值是.

查看试题解析
24.

(1)、如图①，点C是 $A B$ 中点， $C D ⊥ A B$ ，P是 $C D$ 上任意一点，则线段 $P A$ 与 $P B$ 的数量关系是．

(2)、如图②，在平面直角坐标系中，直线 $y = - \frac{1}{3} x + 1$ 分别交x轴、y轴于点A和点B ，点C是 $A B$ 中点， $C D ⊥ A B$ 交 $O A$ 于点D ，连接 $B D$ ，求 $B D$ 的长．

(3)、如图③，①将线段 $A B$ 绕点A顺时针旋转 $90 °$ 得到线段 $A B^{'}$ ，请在图③网格中画出线段 $A B^{'}$ ；
②若存在一点P ，使得 $P A = P B^{'}$ ，且 $∠ A P B^{'} \neq 90 °$ ，当点P的横、纵坐标均为整数时，则 $A P$ 长度的最小值为 ▲ ．

查看试题解析
25. 如图，在等边 $△ A B C$ 中， $A B = 6$ ．点P从点A出发以每秒2个单位的速度沿边 $A B$ 向终点B运动，过点P作 $P D ⊥ A C$ 于点D ，过点P向上作 $P F / / A C$ ，且 $P F = \sqrt{3} P D$ ，以 $P F$ 、 $P D$ 为边作矩形 $P D E F$ ．设点P的运动时间为x（秒），矩形 $P D E F$ 与 $△ A B C$ 的重叠部分图形的面积为y ．

(1)、用含x的式子表示线段 $P D$ 的长；

(2)、求出当点F落在边 $B C$ 上时x的值；

(3)、求在运动过程中y与x之间的函数关系式．

查看试题解析
26. 如图，在平面直角坐标系中，已知抛物线 $y = x^{2} + b x + c$ 过A ， B ， C三点，点A的坐标是 $(3 ， 0)$ ，点C的坐标是 $(0 ， - 3)$ ，动点P在抛物线上．

(1)、求这个抛物线的解析式及顶点D的坐标；

(2)、是否存在点P ，使得 $△ A C P$ 是以 $A C$ 为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；

(3)、设动点P的横坐标为m ， $△ P A C$ 的面积为S．请直接写出面积S随着m的增大而减小时m的取值范围．

查看试题解析

x	…	－5	－4	－3	－2	－1	0	…
y	…	4	0	－2	－2	0	4	…