广东省深圳市盐田区2021年中考数学一模试卷
试卷更新日期:2021-05-28 类型:中考模拟
一、单选题
-
1. 9的算术平方根是( )A、3 B、-3 C、±3 D、812. 黄河发源于巴颜喀拉山脉北麓,注入渤海,流域面积约为750000km2 . 将750000用科学记数法表示为( )A、75× B、7.5× C、7.5× D、0.75×3. 在-3, ,3.14, , , ,0.1010010001 这 7 个数中,无理数共有( )A、2 个 B、3 个 C、4 个 D、5 个4. 如图,该几何体是由5个形状大小相同的正方体组成,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 下列运算正确的是( )A、2a+3b=5ab B、5 -3 =2 C、 = D、 = -46. 如图,将一副三角板按不同位置摆放,其中α和β互为余角的是( )A、
5. 下列运算正确的是( )A、2a+3b=5ab B、5 -3 =2 C、 = D、 = -46. 如图,将一副三角板按不同位置摆放,其中α和β互为余角的是( )A、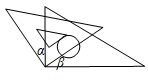 B、
B、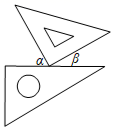 C、
C、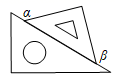 D、
D、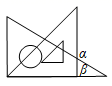 7. 今年3月12日,某学校开展植树活动,某植树小组20名同学的年龄情况如下表:
7. 今年3月12日,某学校开展植树活动,某植树小组20名同学的年龄情况如下表:年龄(岁)
12
13
14
15
16
人数
1
4
3
5
7
则这20名同学年龄的众数和中位数分别是( )
A、15,14 B、15,15 C、16,14 D、16,158. 在平面直角坐标系中,点 A(-6,1),B(2,2),C 分别在不同的象限.若反比例函数的图象经过其中两点,则点 C 的坐标可能是( )A、(-3,2) B、(3,﹣2) C、(﹣1,4) D、(4,-1)9. 如图,抛物线y=a +bx+c与直线y=kx交于M , N两点,则二次函数y=a +(b﹣k)x+c的图象可能是( ) A、
A、 B、
B、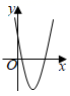 C、
C、 D、
D、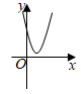 10. 如图,已知 M(0,2),A(2,0),以点 M 为圆心,MA 为半径作⊙M , 与 x 轴的另一个交点为 B , 点 C 是⊙M 上的一个动点,连接 BC , AC , 点 D 是 AC 的中点,连接 OD . 给出 4 个说法:①BC=2OD;②∠ODA=45°;③当线段 OD 取得最大值时,点 D 的坐标为(1,1+ );④当点 C 在 上运动时,点 D 的运动路径为 .其中正确的是( )
10. 如图,已知 M(0,2),A(2,0),以点 M 为圆心,MA 为半径作⊙M , 与 x 轴的另一个交点为 B , 点 C 是⊙M 上的一个动点,连接 BC , AC , 点 D 是 AC 的中点,连接 OD . 给出 4 个说法:①BC=2OD;②∠ODA=45°;③当线段 OD 取得最大值时,点 D 的坐标为(1,1+ );④当点 C 在 上运动时,点 D 的运动路径为 .其中正确的是( ) A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
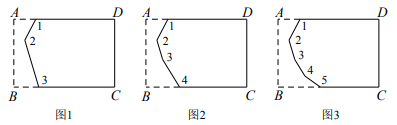
11. 分解因式: -6 +9m= .12. 一个口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,放回搅匀,再摸出第2个球,则两次都摸出白球的概率为 .13. 对于有理数 x , y , 定义新运算“※”:x※y=ax+by+1(a , b 为常数),若 3※4=9,4※7=5,则 7※11= .14. 若关于 的一元二次方程 有实数根,则 的取值范围为.15. 如图,如图1将矩形ABCD剪2刀得3个角,其和为360°;如图2,剪3刀得4个角,其和为540°; 如图 3,剪4刀得5个角,其和为720°……按上述剪法剪n刀得(n+1)个角,其和为 .
三、解答题
-
16. 计算: .17. 先化简,再代入求值: ,其中 x=2021.18. 某校对七年级部分学生进行了随机问卷调查,其中一个问题是“你每周在家参加家务劳动的时间是多少?”,共有如下四个选项: A.1 小时以下 B.1~2 小时(不包含 2 小时) C.2~3 小时(包含 2 小时) D.3 小时以上 图①、图②是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
 (1)、填空:本次问卷调查一共调查了名学生;(2)、请将图①的条形统计图补充完整,并求出图②中D部分所对应的圆心角度数;(3)、若该校共有1800名学生,请你估计全校每周在家参加家务劳动时间不低于2小时的学生人数.19. 如图,AB是⊙O的直径,点C为圆上一点,过圆心O作弦BC的垂线,交过点C的切线 于点D , OD交⊙O于点E , 连接AC , BD .
(1)、填空:本次问卷调查一共调查了名学生;(2)、请将图①的条形统计图补充完整,并求出图②中D部分所对应的圆心角度数;(3)、若该校共有1800名学生,请你估计全校每周在家参加家务劳动时间不低于2小时的学生人数.19. 如图,AB是⊙O的直径,点C为圆上一点,过圆心O作弦BC的垂线,交过点C的切线 于点D , OD交⊙O于点E , 连接AC , BD . (1)、求证:BD是⊙O的切线;(2)、若AC=AO=3,求阴影部分的面积.20. 某超市用4000元购进某种牛奶,面市后供不应求,超市又用1万元购进第二批这种牛奶, 所购数量是第一批的2倍,但单价贵了2元.(1)、第一批牛奶进货单价为多少元?(2)、超市销售两批牛奶售价相同,两批全部售完后要求获利不少于4000元,则售价至少为多少元?21. 问题呈现: 如图1,在边长为1的正方形网格中,分别连接格点A , B和C , D , AB和CD相交于点P , 求tan∠BPD 的值.
(1)、求证:BD是⊙O的切线;(2)、若AC=AO=3,求阴影部分的面积.20. 某超市用4000元购进某种牛奶,面市后供不应求,超市又用1万元购进第二批这种牛奶, 所购数量是第一批的2倍,但单价贵了2元.(1)、第一批牛奶进货单价为多少元?(2)、超市销售两批牛奶售价相同,两批全部售完后要求获利不少于4000元,则售价至少为多少元?21. 问题呈现: 如图1,在边长为1的正方形网格中,分别连接格点A , B和C , D , AB和CD相交于点P , 求tan∠BPD 的值.方法归纳: 利用网格将线段CD平移到线段BE , 连接AE , 得到格点△ABE , 且AE⊥BE , 则∠BPD 就变换成Rt△ABE 中的∠ABE .
 (1)、问题解决:
(1)、问题解决:图1中tan∠BPD的值为;
(2)、如图2,在边长为1的正方形网格中,分别连接格点A , B 和 C , D , AB与CD交于点P , 求cos ∠BPD的值;(3)、思维拓展:如图3,AB⊥CD , 垂足为B , 且AB=4BC , BD=2BC , 点E在AB上,且AE=BC , 连接AD交CE的延长线于点P , 利用网格求sin∠CPD .
22. 如图,在平面直角坐标系中,抛物线 :y=- +4与x轴负半轴交于点A , 以点A为顶点作抛物线 :y=- +bx+c , 交 于点 B . (1)、求 b , c 的值;(2)、过 上A , B 之间一点C作x轴的垂线交 于点D . 当线段CD取最大值时,求点C的坐标和CD的长;(3)、在(2)的条件下,是否存在 上一点P与 上一点Q , 使得以点C , D , P , Q为顶点的四边形为平行四边形?若存在,直接写出P , Q的横坐标;若不存在,说明理由.
(1)、求 b , c 的值;(2)、过 上A , B 之间一点C作x轴的垂线交 于点D . 当线段CD取最大值时,求点C的坐标和CD的长;(3)、在(2)的条件下,是否存在 上一点P与 上一点Q , 使得以点C , D , P , Q为顶点的四边形为平行四边形?若存在,直接写出P , Q的横坐标;若不存在,说明理由.