山西省临汾市洪洞县2021年中考数学三模试卷
试卷更新日期:2021-05-28 类型:中考模拟
一、单选题
-
1. 计算-2-7的结果是( )A、 B、9 C、 D、52. 在“算经十书”中,《九章算术》是中国古代记载最全面完整的一部著作,它的出现标志中国古代数学形成了完整的体系,而《海岛算经》则是中国最早的一部测量数学专著,使“中国在数学测量学的成就,超越西方约一千年”,这两本著作是下列哪位数学家留给后世的宝贵数学遗产.( )A、
 杨辉
B、
杨辉
B、 祖冲之
C、
祖冲之
C、 秦九韶
D、
秦九韶
D、 刘徽
3. 下列运算错误的是( )A、 B、 C、 D、4. 电池是能将化学能转化成电能的能量来源装置,在人们日常生活中发挥着重要作用.如图所示,是手电筒中经常使用的锂电池实物图,其形状呈圆柱形,则该物体的俯视图为( )
刘徽
3. 下列运算错误的是( )A、 B、 C、 D、4. 电池是能将化学能转化成电能的能量来源装置,在人们日常生活中发挥着重要作用.如图所示,是手电筒中经常使用的锂电池实物图,其形状呈圆柱形,则该物体的俯视图为( ) A、
A、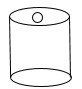 B、
B、 C、
C、 D、
D、 5. 科学家构建的一台76个光子100个模式的量子计算机,它处理“高斯玻色取样”的速度比目前最快的超级计算机“富岳”快100万亿倍.即超级计算机需要一亿年完成的任务,“九章”只需一分钟完成.将数据“100万亿”用科学记数法可表示为( )A、 B、 C、 D、6. 将一副三角板按如图所示摆放,直角三角尺 的锐角顶点A与另一三角尺 的直角顶点重合在一起,(其中 , ),直角边 与 交于点E,若 ,则 的度数为( ).
5. 科学家构建的一台76个光子100个模式的量子计算机,它处理“高斯玻色取样”的速度比目前最快的超级计算机“富岳”快100万亿倍.即超级计算机需要一亿年完成的任务,“九章”只需一分钟完成.将数据“100万亿”用科学记数法可表示为( )A、 B、 C、 D、6. 将一副三角板按如图所示摆放,直角三角尺 的锐角顶点A与另一三角尺 的直角顶点重合在一起,(其中 , ),直角边 与 交于点E,若 ,则 的度数为( ).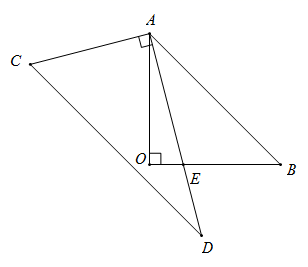 A、 B、 C、 D、7. 蝶,通称为“蝴蝶”,属于节肢动物,体表具有分节的外骨骼,身体分为头、胸、腹三个部分,胸部长有两对翅膀,翅膀上各式各样的色彩上和斑纹是由翅膀上的鳞片组成.如图,是一只蝴蝶标本,已知表示蝴蝶两“翅膀尾部”A、B两点的坐标分别为 , ,则表示蝴蝶身体“尾部”C点的坐标为( )
A、 B、 C、 D、7. 蝶,通称为“蝴蝶”,属于节肢动物,体表具有分节的外骨骼,身体分为头、胸、腹三个部分,胸部长有两对翅膀,翅膀上各式各样的色彩上和斑纹是由翅膀上的鳞片组成.如图,是一只蝴蝶标本,已知表示蝴蝶两“翅膀尾部”A、B两点的坐标分别为 , ,则表示蝴蝶身体“尾部”C点的坐标为( )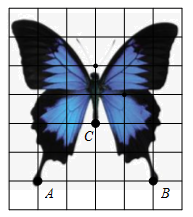 A、 B、 C、 D、8. 山西苹果产地主要集中在曲沃、襄汾、新绛、万荣、临猗、平陆等地,其中,以临猗苹果和万荣苹果较为著名.为了解不同品种苹果树的产量及稳定程度,某果园随机从甲、乙、丙、丁四个品种中各采摘了10棵树的苹果,每棵产量的平均数 (单位:千克)及方差 (单位: )如表所示:
A、 B、 C、 D、8. 山西苹果产地主要集中在曲沃、襄汾、新绛、万荣、临猗、平陆等地,其中,以临猗苹果和万荣苹果较为著名.为了解不同品种苹果树的产量及稳定程度,某果园随机从甲、乙、丙、丁四个品种中各采摘了10棵树的苹果,每棵产量的平均数 (单位:千克)及方差 (单位: )如表所示:甲
乙
丙
丁
160
200
180
170
2.7
1.8
3.1
1.8
若计划从四个品种中选择一种苹果树进行种植,根据苹果树的产量及稳定程度,较为合适品种是( )
A、甲 B、乙 C、丙 D、丁9. 如图,在平面直角坐标系中,二次函数 的图象经过正方形 的三个顶点A、B、C,A点为顶点,将该抛物线经过平移,使其顶点为C点,则平移后抛物线的表达式为( )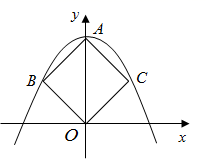 A、 B、 C、 D、10. 如图,将半径为2,圆心角为 的扇形 绕A点逆时针旋转,在旋转过程中,点B落在扇形 的弧 的点 处,点C的对应点为点 ,则阴影部分的面积为( )
A、 B、 C、 D、10. 如图,将半径为2,圆心角为 的扇形 绕A点逆时针旋转,在旋转过程中,点B落在扇形 的弧 的点 处,点C的对应点为点 ,则阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 化简: .12. 中国北斗卫星导航系统是中国自行研制的全球卫星导航系统.是继美国全球定位系统( )、俄罗斯格洛纳斯卫星导航系统( )之后第三个成熟的卫星导航系统.在发射前,对我国最后一颗北斗卫星各零部件的调查,最适合采用的调查方式是 . (填“普查”或“抽样调查”)13. 如图,是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成…按此规律排列下去,则第n个图案中的基础图形个数为 . (用n的代数式表示)
 14. 如图,点A在双曲线 上,过点A作 轴于点B,点C在线段 上且 ,双曲线 经过点C,则k的值为 .
14. 如图,点A在双曲线 上,过点A作 轴于点B,点C在线段 上且 ,双曲线 经过点C,则k的值为 .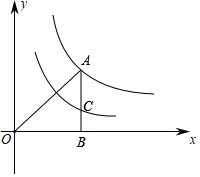 15. 如图所示,在 中, , , ,将 绕点C逆时针旋转 得到 ,连接 , ,并延长 交 于点D,则 的长为 .
15. 如图所示,在 中, , , ,将 绕点C逆时针旋转 得到 ,连接 , ,并延长 交 于点D,则 的长为 .
三、解答题
-
16.(1)、计算:(2)、下面是小颖同学解一元一次不等式 的解答过程,请认真阅读并完成相应任务.
解: ,第一步
,第二步
,第三步
,第四步
任务一:填空:①以上运算步骤中,第步是进行去分母,去分母的依据是
②第步开始出现错误,这一步错误的原因是;
任务二:请直接写出正确的计算结果;
任务三:除纠正上述错误外,请你根据平时的学习经验,解一元一次不等式时,还需要注意的事项给其他同学提一条建议 .
17. 阅读下列材料,并按要求完成相应的任务.你知道“皮克定理”吗?
“皮克定理”是奥地利数学家皮克(如图1)发现的一个计算点阵中多边形的面积公式.在一张方格纸上,上面画着纵横两组平行线,相邻平行线之间的距离都相等,这样两组平行线的交点,就是所谓格点.一个多边形的顶点如果全是格点,这个多边形就叫做格点多边形.有趣的是,这种格点多边形的面积计算起来很方便,只要数一下图形边线上的点的数目及图内的点的数目,就可用公式算出.即 ,其中a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积.(利用图2中的多边形可以验证)这个公式是奥地利数学家皮克在1899年发现的,被称为“皮克定理”.
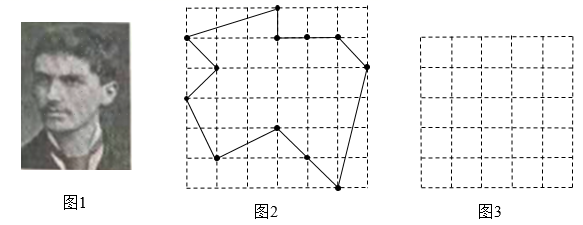
任务:
(1)、如图2,是 的正方形网格,且小正方形的边长为1,利用“皮克定理”可以求出图中格点多边形的面积是 .(2)、已知:一个格点多边形的面积S为19,且边界上的点数b是内部点数a的3倍,则 .(3)、请你在图3中设计一个格点多边形.要求:①格点多边形的面积为8;②格点多边形是一个轴对称图形.18. 为积极响应国家提倡的“绿色”、“环保”、“节能”的人类生活新标准,智能家居逐步进入公众视野.智能家居是以住宅为平台,利用综合布线技术、网络通信技术、安全防范技术、自动控制技术、音视频技术将家居生活有关的设施集成,构建高效的住宅设施与家庭日程事务的管理系统,提升家居安全性、便利性、舒适性、艺术性,并实现环保节能的居住环境,根据所给信息,回答下列问题: (1)、根据图1所给信息解答下列问题:
(1)、根据图1所给信息解答下列问题:①图中2016-2022年全球智能家居市场规模的中位数是 ▲ 亿美元;
②试计算2020-2021年市场规模的增长率(精确到 );
③请你根据图表信息简单描述智能家居的市场规模情况,并对未来市场做出预测;
(2)、如图2,中国贵州的“扬子智能家居”有八大控制系统.厂家为作宣传,特举办如下活动:将其中的三个控制系统制成编号为W、X、Q的三张卡片(除编号和内容外完全相同).他们将三张卡片背面朝上,洗匀放好,顾客从中随机抽取一张放回,再从中抽取一张.若抽到的两张卡片恰好是“智能音箱系统”和“智能安防系统”,则可获奖.请用列表或画树状图的方法求出顾客获奖的概率.


W.门窗系统
X.音箱系统
Q.安防系统
19. 如图,是小清同学的数学笔记,任细阅读并完成任务:在平行四边形 中, ,求作菱形,使点E、点F分别在 、 边上.(尺规作图,保留作图痕迹)

办法一:
以点B为圆心, 长为半径,画弧交 于点E,再分别以点A、E为圆心,大于 的相同长为半径画弧,两弧交于点P;连接 并延长交 于点F,连接 ,则所得四边形 是菱形.
办法二:
连接 ,分别以A、C为圆心,大于 的长为半径作弧,两弧交于M、N两点;连接 ,分别与 、 、 交于E、F、O三点;连接 、 .则四边形 是菱形.
任务:
(1)、填空:“办法一”中,判别四边形 是菱形的数学依据是;(2)、在图2中,根据“办法二”的作图方法,使用直尺和圆规补全图形(保留作图痕迹);(3)、写出“办法二”的推理过程.20. 汾河古称“汾”,又称汾水,黄河的第二大支流,汾者,大也,汾河因此而得名.今年1月20日,太原市启动了史上规模最大的城市管理全面提升行动,对汾河景区进行大修改造和综合提升.现对一段全长为1200米的河岸进行植树造林,植树400米后、为了尽快完成任务,后来每天的工作效率比原计划提高 ,结果共用13天完成植树造林任务.(1)、求原计划每天植树造林多少米?(2)、若承包商原来每天支付工人工资为1500元,提高工作效率后每天支付给工人的工资增长了 ,完成整个工程后承包商共支付工人工资多少元?21. 如图, 是 的直径,点D是直径 上不与A,B重合的一点,过点D作 ,且 ,连接 ,交 于点F,在 上取一点E,使 .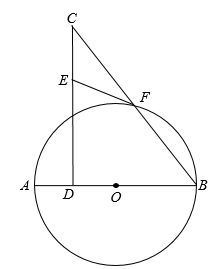 (1)、求证: 是 的切线;(2)、当D是 的中点, 时,求 的长.22. 综合与实践背景阅读:
(1)、求证: 是 的切线;(2)、当D是 的中点, 时,求 的长.22. 综合与实践背景阅读:“旋转”即物体绕一个点或一个轴做圆周运动.在中国古典专著《百喻经·口诵乘船法而不解用喻》中记载:“船盘回旋转,不能前进.”而图形旋转即:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转,这个定点叫做旋转中心,转动的角叫做旋转角.综合实践课上,“睿智”小组专门探究了正方形的旋转,情况如下:在正方形 中,点O是线段 上的一个动点,将正方形 绕点O顺时针旋转得到正方形 (点 , , , 分别是点A,B,C,D的对应点).设旋转角为 ( ).
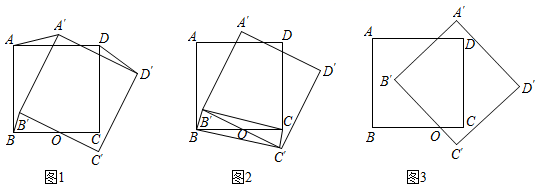 (1)、操作猜想:
(1)、操作猜想:如图1,若点O是 中点,在正方形 绕点旋转过程中,连接 , , ,则线段 与 的数量关系是;线段 与 的数量关系是 .
(2)、探究验证:如图2,在(1)的条件下,在正方形 绕点 旋转过程中,顺次连接点B, ,C, ,B.判断四边形 的形状,并说明理由.
(3)、拓展延伸:如图3,若 ,在正方形 绕点O顺时针旋转的过程中,设直线 交线段 于点P.连接 ,并过点 作 于点Q.请你补全图形,并直接写出 的值.
23. 综合与探究在平面直角坐标系中,二次函数 的图象与x轴交于 , 两点,与y轴交于点C.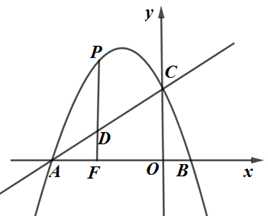 P(1)、求抛物线与直线 的函数解析式;(2)、若点P是直线 上方抛物线上的一动点,过点P作 轴于点F,交直线 于点D,求线段 的最大值.(3)、点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
P(1)、求抛物线与直线 的函数解析式;(2)、若点P是直线 上方抛物线上的一动点,过点P作 轴于点F,交直线 于点D,求线段 的最大值.(3)、点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.