辽宁省沈阳市铁西区2021年中考数学一模试卷

试卷更新日期：2021-05-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 一5的绝对值是（）

A、5 B、 $\frac{1}{5}$ C、 $- \frac{1}{5}$ D、－5

查看试题解析
2. 据报道，我国自1981年开展全民义务植树运动以来，截至目前我国约有1643000万人次参与全民义务植树运动，人工林面积稳居全球第一．数据“1643000”用科学记数法表示为（）

A、 $1.643 \times 10^{5}$ B、 $16.43 \times 10^{6}$ C、 $16.43 \times 10^{3}$ D、 $1.643 \times 10^{6}$

查看试题解析
3. 如图，是由5个大小相同的小立方块搭成的几何体，其主视图是（）

A、 B、 C、 D、

查看试题解析
4. 以下调查中，最适合采用全面调查的是（）

A、调查某城市居民2月份人均网上购物的次数 B、调查全国中学生的平均身高 C、检测即将发射的一颗气象卫星的零部件质量 D、检测某城市的空气质量

查看试题解析
5. 方程组 ${\begin{array}{l} x - y = 4 \\ 2 x + y = 2 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 \\ y = - 2 \end{array}$ B、 ${\begin{array}{l} x = 4 \\ y = 0 \end{array}$ C、 ${\begin{array}{l} x = - 2 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$

查看试题解析
6. 如图， $A B / / C D$ ，点E是 $C D$ 上一点，点F是 $A B$ 上一点， $E G$ 是 $∠ F E D$ 的平分线，交直线 $A B$ 于点G．若 $∠ G F E = 66 °$ ，则 $∠ E G F$ 的大小为（）

A、 $47 °$ B、 $57 °$ C、 $66 °$ D、 $67 °$

查看试题解析
7. 一个不透明的袋子中装有12个小球，其中8个红球，3个绿球，1个白球，这些球除颜色外其它都相同．从袋子中随机摸出一个小球，摸出的球是红球的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{8}$

查看试题解析
8. 一次函数 $y = a x + a$ 与反比例函数 $y = \frac{- a}{x} (a \neq 0)$ 在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
9. 已知关于x的一元二次方程 $x^{2} - 2 \sqrt{6} x + k = 0$ 有两个相等的实数根，则k的值为（）

A、3 B、 $\pm 6$ C、6 D、 $\pm 3$

查看试题解析
10. 在平面直角坐标系中，将二次函数 $y = x^{2}$ 的图象向左平移2个单位，再向下平移2个单位，下列点在平移后的图象上的是（）

A、 $(- 1 ， 2)$ B、 $(- 2 ， - 2)$ C、 $(1 ， - 1)$ D、 $(2 ， 2)$

查看试题解析

二、填空题

11. 因式分解： $a b^{2} - 16 a =$ ．

查看试题解析
12. 甲，乙，丙，丁四位同学10次数学测验成绩统计如右表所示，如果从这四位同学中，选出一位平均成绩高且成绩稳定的同学参加数学竞赛，那么应选去．

甲

乙

丙

丁

平均分/分

86

90

90

85

方差

24

36

42

38

查看试题解析
13. 如图，在 $△ A B C$ 中，点 $D ， E$ 分别是 $A C ， B C$ 的中点，点F是 $D E$ 上一点，连接 $A F ， C F$ ，且 $A F ⊥ C F$ ，若 $A C = 6 ， E F = 1$ ，则 $A B =$ ．

查看试题解析
14. 星期天小明步行从家去图书馆，中间要路过超市，小明以a米/分钟的速度匀速到达超市，再以b米/分钟的速度匀速到达图书馆，图中的折线 $O A B$ 反映了小明从家步行到图书馆所走的路程s（米）与时间t（分钟）的函数关系，根据图象提供的信息， $\frac{a}{b}$ 的值为．

查看试题解析
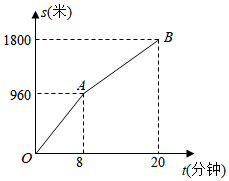15. 如图，半径为6的扇形 $O A B$ 中， $∠ A O B = 90 °$ ，点C为 $A B$ 上一点， $C D ⊥ O A ， C E ⊥ O B$ ，垂足分别为点 $D ， E$ ．若 $∠ C E D = 40 °$ ，则图中阴影部分的面积为．

查看试题解析
16. 如图1，在矩形 $A B C D$ 中，点E是 $A D$ 边中点，点P是对角线 $A C$ 上一动点，连接 $P D ， P E$ ，设 $P C = x ， P D + P E = y ， y$ 关于x的全部函数图象如图2所示，其中点N是图象上的最低点，则点N的纵坐标为．

查看试题解析

三、解答题

17. 计算： $| 1 - \sqrt{3} | + 3 \tan 30 ° - \sqrt{12} + {(π - 2021)}^{0}$ ．

查看试题解析
18. 如图， $B D$ 是正方形 $A B C D$ 的对角线，点E在 $△ B C D$ 内部，连接 $B E ， C E ， ∠ B C E = ∠ D B E$ ，求 $∠ B E C$ 的度数．

查看试题解析
19. 在学校举办的“美德少年”评选活动中，九年一班有甲，乙，丙，丁共4名学生获奖，其中甲为小明．班主任决定在这4名获奖学生中随机选出2名学生在班级进行主题演讲，请用树状图法或列表法求小明被选中进行主题演讲的概率．

查看试题解析
20. 某校即将举行校园艺术节活动，拟定了 $A ， B ， C ， D$ 四种活动方案，为了解学生对方案的意见，学校随机抽取了部分学生进行问卷调查（每人必须且只能赞成种方案），将调査结果进行统计并绘制成如图两幅不完整的统计图．
请根据统计图中的信息，解答下列问题：

(1)、求抽取的学生总人数；

(2)、抽取的学生中，赞成A活动方案的人数为人；扇形统计图中赞成D活动方案所在扇形的圆心角的度数为°；

(3)、补全条形统计图；

(4)、若该校有学生1800人，估计赞成B活动方案的学生共有多少人．

查看试题解析
21. 甲、乙两支工程队修建公路，已知甲队每天修路的长度比乙队每天修路的长度多50米，甲队修路600米与乙队修路300米用的天数相同．

(1)、求甲、乙两支工程队每天各修路多少米？

(2)、计划修建长度为3600米的公路，因工程需要，甲、乙两支工程队都要参与这条公路的修建．若甲队每天所需费用为1.2万元，乙队每天所需费用为0.5万元，在总费用不超过40万元的情况下，至少安排乙队施工天．

查看试题解析
22. 如图，在 $△ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径的 $⊙ O$ 分别交 $A C ， B C$ 于点 $D ， E$ ，点F在 $A C$ 的延长线上，连接 $B F ， ∠ B A C = 2 ∠ C B F$ ．

(1)、求证：直线 $B F$ 是 $⊙ O$ 的切线；

(2)、若 $O A = C F = 3$ ，求 $△ B C F$ 的面积．

查看试题解析
23. 如图，在平面直角坐标系中，直线 $y = 2 x + 6$ 与x轴交于点A，直线 $y = - 2 x + 3$ 与x轴交于点B，与y轴交于点C，与直线 $y = 2 x + 6$ 交于点D．

(1)、求点D的坐标；

(2)、将 $△ B O C$ 沿x轴向左平移，平移后点B的对应点为点E，点O的对应点为点F，点C的对称点为点G，当点F到达点A时，停止平移，设平移的距离为t．
①当点G在直线 $y = 2 x + 6$ 上时，求 $△ D C G$ 的面积；

②当 $△ E F G$ 与四边形 $A O C D$ 重合部分的面积为2时，请直接写出 $t$ 的值．

查看试题解析
24. $△ A B C$ 为等边三角形， $A B = 8 ， A D ⊥ B C$ 于点D，点E为线段 $A D$ 上一点， $A E = 2 \sqrt{3}$ ．以 $A E$ 为边作等边三角形 $A E F$ ，连接 $C E ， N$ 为 $C E$ 的中点．

(1)、如图1，当点E和点F在直线 $A C$ 两侧时， $E F$ 与 $A C$ 交于点M，连接 $M N$ ，
①求证： $M E = M F$ ；

②求线段 $M N$ 的长；

(2)、将图1中的 $△ A E F$ 绕点A逆时针旋转，旋转角为 $α$ ，点M为线段 $E F$ 的中点，连接 $B E ， M N ， D M$ ，
①如图2，当 $α = 90 °$ 时，请直接写出 $\frac{D M}{B E}$ 的值；

②连接 $B N$ ，在 $△ A E F$ 绕点A逆时针旋转过程中，当线段 $B N$ 最大时，请直接写出 $\tan ∠ D A N$ 的值．

查看试题解析
25. 如图，抛物线 $y = \frac{2}{15} x^{2} + b x - 6$ 与 $y$ 轴交于点 A，与x轴正半轴交于点 $B (10 \sqrt{3} ， 0)$ ，点 C在线段 $O B$ 上，连接 $A C$ ，过点B作 $B E / / A C$ 交 y轴于点 E，点 $M ， N$ 在线段 $B E$ 上，且点M在点 $B ， N$ 之间， $B M ： E N = 2 ： 3$ ．点 $P ， Q$ 分别是线段 $A C ， M N$ 上的动点，当点 P从点A匀速运动到点 C时，点Q恰好从点M匀速运动到点N，设 $Q N = m ， P A = n$ ，已知 $n = - \frac{6}{5} m + 12$ ．

(1)、求抛物线的对称轴；

(2)、求线段 $A C$ 和 $B E$ 的长；

(3)、连接 $A B$ ，当直线 $P Q$ 经过 $△ A O B$ 的一个顶点时，请直接写出直线 $P Q$ 与抛物线对称轴交点的纵坐标．

查看试题解析

	甲	乙	丙	丁
平均分/分	86	90	90	85
方差	24	36	42	38