辽宁省大连市金州区2021年中考数学一模试卷

试卷更新日期：2021-05-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个数中，最大的数是（）

A、1 B、0 C、 $- \frac{1}{2}$ D、 $- 1$

查看试题解析
2. 在平面直角坐标系中，点 $P (- 3 ， 1)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知α为锐角，若 $\sin α = \frac{\sqrt{3}}{2}$ ，则α的度数是（）

A、30° B、45° C、60° D、75°

查看试题解析
4. 下列四个几何体中，左视图是三角形的几何体（）

A、 B、 C、 D、

查看试题解析
5. 数字13.91万，用科学记数法应表示为（）

A、 $1.391 \times 10^{6}$ B、 $1.391 \times 10^{5}$ C、 $1.391 \times 10^{2}$ D、 $1.391 \times 10^{3}$

查看试题解析
6. 已知 $A B / / C D$ ，CE平分 $∠ A C D$ ，交AB于点E ， $∠ A = 124 °$ ，则 $∠ 1$ 的度数为（）

A、 $56 °$ B、 $38 °$ C、 $36 °$ D、 $28 °$

查看试题解析
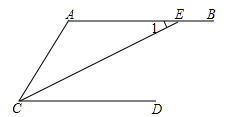7. 下列运算正确的是（）

A、 ${(a - 2)}^{2} = a^{2} - 4$ B、 $a^{2} \cdot a^{4} = a^{8}$ C、 $a^{3} + a^{2} = 2 a^{5}$ D、 ${(- a b^{2})}^{3} = - a^{3} b^{6}$

查看试题解析
8. 把标号为1，2，3的三个小球放入一个不透明的口袋中，随机摸取一个小球然后放回，再随机摸出一个小球，两次取出的小球的标号的和大于3的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{4}{9}$ C、 $\frac{5}{9}$ D、 $\frac{2}{3}$

查看试题解析
9. 二次函数 $y = a x^{2} + b x + c$ （a ， b ， c是常数 $a \neq 0$ ）的自变量x与函数值y的部分对应值如下表：

x

…

$- 1$

0

1

3

…

$y = a x^{2} + b x + c$

…

n

3

m

3

…

且当 $x = \frac{3}{2}$ 时，与其对应的函数值 $y < 0$ ．则（）

A、 $m < n$ B、 $m = n$ C、 $m > n$ D、无法判断

查看试题解析
10. 如图，正方形纸片ABCD的边长为5，E是边BC的中点，连接AE ．沿AE折叠该纸片，使点B落在F点．则CF（）

A、 $\frac{5}{2}$ B、2 C、 $\sqrt{5}$ D、 $\sqrt{3}$

查看试题解析

二、填空题

11. 不等式x﹣2≤0的解集是．

查看试题解析
12. 定义： $f (x) = \frac{2 x - 1}{3}$ ，则 $f (3)$ 的值是．

查看试题解析
13. 若一组数据4，9，5，m ， 3的平均数是5，则这组数据的众数是．

查看试题解析
14. 如图，在平行四边形ABCD中，点E在DA的延长线上，且 $A E = \frac{1}{3} A D$ ，连接CE交BD于点F ，交AB于点G ，则 $S_{△ B G C} ： S_{四边形 A D C G}$ 的值是．

查看试题解析
15. 如图，在 $R t △ O A B$ 中， $∠ O A B = 90 ° ， O A = 6 ， A B = 4$ ，边OA在x轴上，若双曲线 $y = \frac{k}{x}$ 经过边OB上一点 $D (4 ， m)$ ，则k值为．

查看试题解析
16. 如图， $△ A B C$ 中， $A B = 4 ， B C = 2$ ，边AC上取点D ，且 $D B = B C$ 、 $∠ D B C = ∠ B A C$ ，P是边BC延长线上一点，过点P作 $P Q ⊥ B P$ ，交线段BD的延长线于点Q ．设 $C P = x ， D Q = y$ ．则y关于x的函数解析式为．

查看试题解析

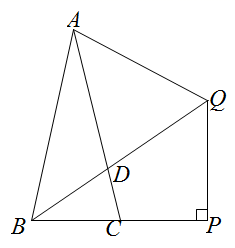
三、解答题

17. 计算： $(\sqrt{3} + 2) (\sqrt{3} - 2) + {(π - 3)}^{0} - \sqrt{12}$

查看试题解析
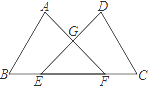
18. 计算： $(x - 4 + \frac{9}{x + 2}) \div \frac{{(x - 1)}^{2}}{x^{2} - 4}$

查看试题解析
19. 如图，点E、F在BC上，BE=CF，AB=DC，∠B=∠C，AF与DE交于点G，求证：GE=GF．

查看试题解析
20. 为了解树苗的数量，园林部门对种植的四类树苗进行了抽样调查，并将调查情况绘制成如下两幅统计图（不完整）．

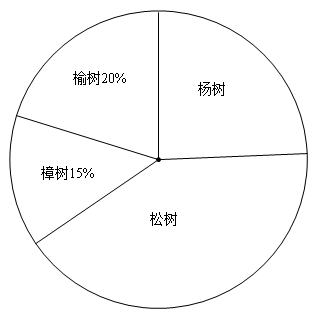
根据图表中的信息解答下列问题：

(1)、被抽查的树苗中，松树有棵，柳树苗占被抽查树苗总数的百分比是 $%$ ；

(2)、此次被抽查的树苗共有棵，若杨树苗所对的圆心角为 $°$ ；

(3)、今年共种树36000棵，松树约有多少棵．

查看试题解析
21. 如图，测量船在点D处，测得小岛最东端（A点处）的方向角为北偏西 $67.5 °$ ，最西端（B点处）的方向角为北偏西 $30 °$ ，已知此时船到直线AB的距离是2000米，根据以上数据，求出小岛东西长度AB的距离（结果取整数，参考数据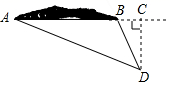： $\sqrt{2} \approx 1.41 ， \sqrt{3} \approx 1.73$ ， $\tan 67.5 ° \approx 2.41 ， \cos 67.5 ° \approx 0.39 ， \sin 67.5 ° \approx 0.92$ ）

查看试题解析
22. 如图，⊙O是△ABC的外接圆，AC是直径，弦BD＝BA，EB⊥DC，交DC的延长线于点E.

(1)、求证：BE是⊙O的切线；

(2)、当sin∠BCE＝ $\frac{3}{4}$ ，AB＝3时，求AD的长.

查看试题解析
23. 小军和爸爸同时从家骑自行车去图书馆，爸爸先以150米/分的速度骑行一段时间，休息了5分钟，再以m米/分的速度到达图书馆，小军始终以同一速度骑行，两人行驶的路程y（米）与时间x（分钟）的关系如图．请结合图象，解答下列问题：

(1)、a=；m= ．

(2)、若小军的速度是120米/分，求小军在图中与爸爸第二次相遇时，距图书馆的距离．

查看试题解析
24. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， B C = 6 ， A C = 8$ ，D是边AB的中点，动点P在线段BA上且不与点A ， B ， D重合，以PD为边构造 $R t △ P D Q$ ，使 $∠ P D Q = ∠ A$ ， $∠ D P Q = 90 °$ ，且点Q与点C在直线AB同侧，设 $B P = x$ ， $△ P D Q$ 与 $△ A B C$ 重叠部分图形的面积为S ．

(1)、当点Q在边BC上时，求BP的长；

(2)、当 $x \leq 7$ 时，求S关于x的函数关系式.

查看试题解析
25. 如图，在正方形ABCD中，点M是边BC上的一点（不与B、C重合），点N在边CD延长线上，且满足 $∠ M A N = 90 °$ ，联结MN ， AC ， MN与边AD交于点E ．

(1)、求证： $A M = A N$

(2)、如果 $∠ C A D = 2 ∠ N A D$ ，求证： $A M^{2} = \sqrt{2} A B \cdot A E$ ；

(3)、MN交AC点O ，若 $\frac{C M}{B M} = k$ ，则 $\frac{O M}{O N} =$ （直接写答案、用含k的代数式表示）．

查看试题解析
26. 在平面直角坐标系中，点A在第一象限， $A B ⊥ y$ 轴于点B ，经过点B的函数图象的一部分（自变量大于0）记为 $G_{1}$ ，将 $G_{1}$ 沿y轴对折，再向下平移两个单位长度得到的图象记为 $G_{2}$ ，图象 $G_{1} ， G_{2}$ 合起来得到的图象记为G ．

(1)、若 $G_{1} ： y = 1 (x > 0)$ ，则OB的长度为：；

(2)、若 $G_{1} ： y = - \frac{1}{2} x^{2} + m x + 1 (x > 0)$ ，其中m是常数，
①则图象 $G_{2}$ 的函数关系式为： ▲ ；

②点 $A 、 A^{'}$ 关于y轴对称且 $A A^{'} = 8$ ，当 $G_{2}$ 与线段 $A A^{'}$ 恰好有一个公共点时，求m的取值范围；

③设G在 $- 4 ⩽ x ⩽ 2$ 上最高点的纵坐标为 $y_{0}$ ，当 $\frac{3}{2} ⩽ y_{0} ⩽ 9$ 时，直接写出m的取值范围．

查看试题解析

x	…	$- 1$	0	1	3	…
$y = a x^{2} + b x + c$	…	n	3	m	3	…