吉林省长春市汽开区2021年中考数学一模试卷
试卷更新日期:2021-05-28 类型:中考模拟
一、单选题
-
1. 如图.数轴上点A对应的数是2,将点A沿数轴向左移动3个单位至点B , 则点B对应的数是( )
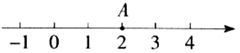 A、-1 B、0 C、3 D、52. 如图,某一时刻“学习强国APP”数据显示阅读量为403000人次.将403000这个数用科学记数法表示为( )
A、-1 B、0 C、3 D、52. 如图,某一时刻“学习强国APP”数据显示阅读量为403000人次.将403000这个数用科学记数法表示为( ) A、 B、 C、 D、3. 如图所示的几何体的俯视图是( )
A、 B、 C、 D、3. 如图所示的几何体的俯视图是( )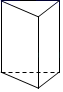 A、
A、 B、
B、 C、
C、 D、
D、 4. 不等式 的解集在数轴上表示正确的是( )A、
4. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. (九章算术)中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”译文:“今有5只雀、6只燕,分别聚集面且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀,6只燕重量为1斤.问雀、燕每只各重多少斤?”设每只雀重x斤,每只燕重y斤,可列方程组为( )A、 B、 C、 D、6. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪.测得旗杆顶的仰角 ;(2)量得测角仪的高度 米;(3)量得测角仪到旗杆的水平距离 米.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
5. (九章算术)中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”译文:“今有5只雀、6只燕,分别聚集面且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀,6只燕重量为1斤.问雀、燕每只各重多少斤?”设每只雀重x斤,每只燕重y斤,可列方程组为( )A、 B、 C、 D、6. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪.测得旗杆顶的仰角 ;(2)量得测角仪的高度 米;(3)量得测角仪到旗杆的水平距离 米.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( ) A、 米 B、 米 C、 米 D、 米7. 如图: .按下列步骤作图:①在射线 上取一点C , 以点O为圆心, 长为半径作圆弧 ,交射线 于点F . 连结 ;②以点F为圆心, 长为半径作圆弧,交弧 于点G;③连结 、 .作射线 .根据以上作图过程及所作图形,下列结论中错误的是( )
A、 米 B、 米 C、 米 D、 米7. 如图: .按下列步骤作图:①在射线 上取一点C , 以点O为圆心, 长为半径作圆弧 ,交射线 于点F . 连结 ;②以点F为圆心, 长为半径作圆弧,交弧 于点G;③连结 、 .作射线 .根据以上作图过程及所作图形,下列结论中错误的是( )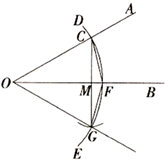 A、 B、 垂直平分 C、 D、8. 如图,矩形 的顶点A、B、C的坐标分别为 、 、 ,将矩形 向右平移t个单位,若平移后的矩形 与函数 ( )的图象有公共点,则t的取值范围是( )
A、 B、 垂直平分 C、 D、8. 如图,矩形 的顶点A、B、C的坐标分别为 、 、 ,将矩形 向右平移t个单位,若平移后的矩形 与函数 ( )的图象有公共点,则t的取值范围是( )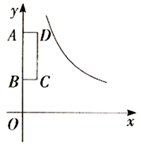 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 计算: .10. 分解因式: .11. 若关于x的一元二次方程 有两个不相等的实数根,则m的取值范围是 .12. 如图,直线 ,直线l与 、 分别交于A、B两点.若 ,则 的大小为 .
 13. 如图,在正五边形 中, .分别以顶点A、B、C、D、E为圆心、 的长为半径在正五边形 内作圆弧,则图中阴影部分图形的面积为 . (结果保留 )
13. 如图,在正五边形 中, .分别以顶点A、B、C、D、E为圆心、 的长为半径在正五边形 内作圆弧,则图中阴影部分图形的面积为 . (结果保留 ) 14. 如图,抛物线 ( )的对称轴为直线 ,该物线交y轴于点A . 交过点A且平行于x轴的直线于另一点B , 过点 且平行于x轴的直线交该抛物线于C、D两点(点C在点D右边),连结 .若点B关于直线 的对称点 恰好落在线段 上,则 的长为 .
14. 如图,抛物线 ( )的对称轴为直线 ,该物线交y轴于点A . 交过点A且平行于x轴的直线于另一点B , 过点 且平行于x轴的直线交该抛物线于C、D两点(点C在点D右边),连结 .若点B关于直线 的对称点 恰好落在线段 上,则 的长为 .
三、解答题
-
15. 先化简,再求值: ,其中 , .16. 现有三张不透明的卡片,其中两张卡片的正面图案为“红旗车新车标”,第三张卡片的正面图案为“红旗车老车标”,卡片除正面图案不同外,其余均相同.将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求两次抽出的卡片上的图案都是“红旗车新车标”的概率.(图案为“红旗车新车标”的两张卡片分别记为 、 ,图案为“红旗车老车标”的卡片记为B)
 17. 图①、图②、图③均是 的正方形网格,每个小正方形的顶点称为格点,线段 的端点均在格点上.只用无刻度的直尺,按要求在图①、图②、图③中以 为边各画一个菱形 .
17. 图①、图②、图③均是 的正方形网格,每个小正方形的顶点称为格点,线段 的端点均在格点上.只用无刻度的直尺,按要求在图①、图②、图③中以 为边各画一个菱形 .要求:菱形 的顶点C、D均在格点上,且所画的三个菱形不全等.
 18. 某扶贫干部决定引进改良的中药种子帮助贫困户脱贫.他先花8000元购买了桔梗种子,又花6000元购买了白术种子,已知他购买的这两种种子质量相等,且桔梗种子比白术种子每千克多20元,求白术种子每千克多少元?19. 如图, 是 的直径, 是 的弦,C为 延长线上的点, .
18. 某扶贫干部决定引进改良的中药种子帮助贫困户脱贫.他先花8000元购买了桔梗种子,又花6000元购买了白术种子,已知他购买的这两种种子质量相等,且桔梗种子比白术种子每千克多20元,求白术种子每千克多少元?19. 如图, 是 的直径, 是 的弦,C为 延长线上的点, . (1)、求证: 是 的切线.(2)、若 的半径为6,求 的长.(结果保留 )20. 4月15日为全民国家安全教育日,为提升学生国家安全意识,某校组织学生参加“国家安全知识竞赛”(满分为100分).竞赛结束后,随机抽取甲、乙两班各40名学生的成绩,并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
(1)、求证: 是 的切线.(2)、若 的半径为6,求 的长.(结果保留 )20. 4月15日为全民国家安全教育日,为提升学生国家安全意识,某校组织学生参加“国家安全知识竞赛”(满分为100分).竞赛结束后,随机抽取甲、乙两班各40名学生的成绩,并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.a . 甲、乙两班各40名学生竞赛成绩的频数分布统计表如下:
成绩
班级
甲
4
10
12
11
3
乙
6
3
15
14
2
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b . 甲班成绩在 这一组的是:
70,70,70,71,72,73,73,73,74,75,76,78
c . 甲、乙两班成绩的平均分、中位数、众数如下:
班级
平均分
中位数
众数
甲
74.2
n
85
乙
73.5
76
84
根据以上信息,回答下列问题:
(1)、表中n的值为 .(2)、在此次测试中,某学生的成绩是74分,在他所属班级排在前20名,由表中数据可知该学生是班的学生(填“甲”或“乙”),理由是 .(3)、按上述统计结果,估计该校1800名学生获得成绩优秀的学生人数.21. 为修建长春地铁,甲、乙两个工程队分别同时开挖两段隧道,所挖隧道的长度y(米)与挖掘时间x(时)之间的函数关系如图所示. (1)、求甲工程队每小时挖隧道的长度.(2)、求乙工程队所挖隧道的长度y(米)与挖掘时间x(时)之间的函数关系式.(3)、当乙工程队比甲工程队多挖5米时,x的值为 .22. (教材呈现)下图是华师版八年级上册数学教材第117页的部分内容.
(1)、求甲工程队每小时挖隧道的长度.(2)、求乙工程队所挖隧道的长度y(米)与挖掘时间x(时)之间的函数关系式.(3)、当乙工程队比甲工程队多挖5米时,x的值为 .22. (教材呈现)下图是华师版八年级上册数学教材第117页的部分内容.把两个全等的直角三角形拼成如图所示的形状,使点A、E、D在同一直线上.利用此图的面积表示式证明勾股定理.
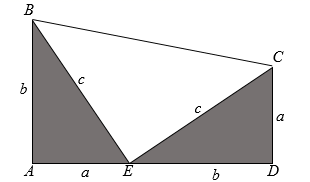
 (1)、(问题解决)根据上面的教材内容,在证明勾股定理的过程中,需要先证明 为等腰直角三角形,请你结合图①,写出证明 为等腰直角三角形的过程.(2)、(拓展应用)如图②,在正方形 中, ,P是对角线 的延长线上一点,以 为直角边在 边的右侧作 ,使 , .若 ,则 , 的面积为 .23. 如图,在 中, , , .动点P从点A出发,沿 方向以每秒2个单位长度的速度向终点B运动,点Q为线段 的中点,过点P作 ,点M在 上方,且 ,以 、 为边作 .设点P的运动时间为t秒.
(1)、(问题解决)根据上面的教材内容,在证明勾股定理的过程中,需要先证明 为等腰直角三角形,请你结合图①,写出证明 为等腰直角三角形的过程.(2)、(拓展应用)如图②,在正方形 中, ,P是对角线 的延长线上一点,以 为直角边在 边的右侧作 ,使 , .若 ,则 , 的面积为 .23. 如图,在 中, , , .动点P从点A出发,沿 方向以每秒2个单位长度的速度向终点B运动,点Q为线段 的中点,过点P作 ,点M在 上方,且 ,以 、 为边作 .设点P的运动时间为t秒. (1)、线段 的长为 , 线段 的长为 .(2)、求 的面积.(用含t的代数式表示)(3)、当线段 与边 有公共点时,求t的取值范围.(4)、当点M到 任意两边所在直线的距离相等时,直接写出此时t的值.24. 在平面直角坐标系中,二次函数 的图象经过点 和 .(1)、求c的值,并用含a的代数式表示b .(2)、当 时,
(1)、线段 的长为 , 线段 的长为 .(2)、求 的面积.(用含t的代数式表示)(3)、当线段 与边 有公共点时,求t的取值范围.(4)、当点M到 任意两边所在直线的距离相等时,直接写出此时t的值.24. 在平面直角坐标系中,二次函数 的图象经过点 和 .(1)、求c的值,并用含a的代数式表示b .(2)、当 时,①求此函数的表达式,并写出函数值y随x的增大而增大时x的取值范围.
②当 时,求y的最大值和最小值.
(3)、若线段 的端点C、D的坐标分别为 、 ,此二次函数的图象与线段 只有一个公共点,直接写出a的取值范围.