黑龙江省绥化市肇东市2021年中考数学一模试卷
试卷更新日期:2021-05-28 类型:中考模拟
一、单选题
-
1. -2020的相反数是( )A、2020 B、 C、 D、2. 若 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、3. 下列说法中,正确的是( )A、“打开电视,正在播放湖北新闻节目”是必然事件 B、某种彩票中奖概率为10%是指买十张一定有一张中奖 C、“明天降雨的概率是50%表示明天有半天都在降雨” D、“掷一次骰子,向上一面的数字是2”是随机事件4. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
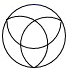 B、
B、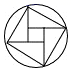 C、
C、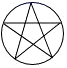 D、
D、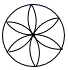 5. 如图是由五个完全相同的小正方体组成的几何体,这个几何体的俯视图是( )
5. 如图是由五个完全相同的小正方体组成的几何体,这个几何体的俯视图是( )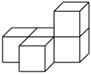 A、
A、 B、
B、 C、
C、 D、
D、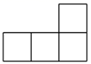 6. 下列计算正确的是( )A、 B、 C、 D、7. 八年级某同学6次数学小测验的成绩分别为95分,80分,85分,95分,95分,85分,则该同学这6次成绩的众数和中位数分别是( )A、95分,95分 B、95分,90分 C、90分,95分 D、95分,85分8. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则S△ECF的值为 ( )
6. 下列计算正确的是( )A、 B、 C、 D、7. 八年级某同学6次数学小测验的成绩分别为95分,80分,85分,95分,95分,85分,则该同学这6次成绩的众数和中位数分别是( )A、95分,95分 B、95分,90分 C、90分,95分 D、95分,85分8. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则S△ECF的值为 ( )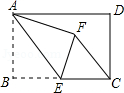 A、 B、 C、 D、9. 温州市为美化城市环境,计划种植树木30万棵,由于志愿者的加入,实际每天植树比原计划多0.2万棵,结果提前5天完成任务,设原计划每天植树x万棵,根据题意可列方程( )A、 B、 C、 D、10. 一个容器有进水管和出水管,每分钟的进水和出水是两个常数.从某时刻开始 内只进水不出水,从第 到第 内既进水又出水,从第 开始只出水不进水,容器内水量y(单位:L)与时间x(单位: )之间的关系如图所示,则图中a的值是( )
A、 B、 C、 D、9. 温州市为美化城市环境,计划种植树木30万棵,由于志愿者的加入,实际每天植树比原计划多0.2万棵,结果提前5天完成任务,设原计划每天植树x万棵,根据题意可列方程( )A、 B、 C、 D、10. 一个容器有进水管和出水管,每分钟的进水和出水是两个常数.从某时刻开始 内只进水不出水,从第 到第 内既进水又出水,从第 开始只出水不进水,容器内水量y(单位:L)与时间x(单位: )之间的关系如图所示,则图中a的值是( ) A、32 B、34 C、36 D、3811. 如图,⊙O的半径为9,四边形ABCD是⊙O的内接四边形,∠B=100°,则劣弧 的长为( )
A、32 B、34 C、36 D、3811. 如图,⊙O的半径为9,四边形ABCD是⊙O的内接四边形,∠B=100°,则劣弧 的长为( )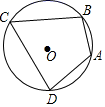 A、4π B、5π C、7π D、8π12. 如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为 ﹣2.其中正确的有( )
A、4π B、5π C、7π D、8π12. 如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为 ﹣2.其中正确的有( )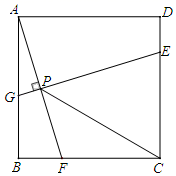 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
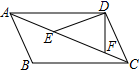
13. 计算 的结果是.14. 用科学记数法表示:-0.00000202=.15. 已知a,b都是实数, ,则ab的值为.16. 若函数y= 与y=x+2图象的一个交点坐标为(a , b),则 的值是 .17. 把多项式a4﹣a2分解因式的结果是18. 如图,在 中, 、 是对角线 上两点, , , ,则 的大小为
 19. 如图,某景区门口的柱子上方挂着一块景点宣传牌CD,宣传牌的一侧用绳子AD和BC牵引着两排小风车,经过测量得到如下数据:AM=2米,AB=4米,∠MAD=45°,∠MBC=30°,则CD的长度约为米.( ≈1.73,结果精确到0.1米)
19. 如图,某景区门口的柱子上方挂着一块景点宣传牌CD,宣传牌的一侧用绳子AD和BC牵引着两排小风车,经过测量得到如下数据:AM=2米,AB=4米,∠MAD=45°,∠MBC=30°,则CD的长度约为米.( ≈1.73,结果精确到0.1米)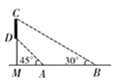 20. 等边 ABC的边长为3,在边AC上取点A1 , 使AA1=1,连接A1B , 以A1B为一边作等边 A1BC1 , 则线段AC1的长为 .21. 如图,在△ABC中,点D,E分别为AB,AC边上一点,且BE=CD,CD⊥BE.若∠A=30°,BD=1,CE=2 ,则四边形CEDB的面积为.
20. 等边 ABC的边长为3,在边AC上取点A1 , 使AA1=1,连接A1B , 以A1B为一边作等边 A1BC1 , 则线段AC1的长为 .21. 如图,在△ABC中,点D,E分别为AB,AC边上一点,且BE=CD,CD⊥BE.若∠A=30°,BD=1,CE=2 ,则四边形CEDB的面积为.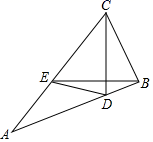 22. 如图,边长为4的等边 ABC , AC边在x轴上,点B在y轴的正半轴上,以OB为边作等边 OBA1 , 边OA1与AB交于点O1 , 以O1B为边作等边 O1BA2 , 边O1A2与A1B交于点O2 , 以O2B为边作等边 O2BA3 , 边O2A3与A2B交于点O3 , …,依此规律继续作等边 On﹣1BAn , 记 OBA1的面积为S1 , O1BA2的面积为S2 , O2BA3的面积为S3 , …, On﹣1BAn的面积为Sn , 则Sn= . (n≥2,且n为整数)
22. 如图,边长为4的等边 ABC , AC边在x轴上,点B在y轴的正半轴上,以OB为边作等边 OBA1 , 边OA1与AB交于点O1 , 以O1B为边作等边 O1BA2 , 边O1A2与A1B交于点O2 , 以O2B为边作等边 O2BA3 , 边O2A3与A2B交于点O3 , …,依此规律继续作等边 On﹣1BAn , 记 OBA1的面积为S1 , O1BA2的面积为S2 , O2BA3的面积为S3 , …, On﹣1BAn的面积为Sn , 则Sn= . (n≥2,且n为整数)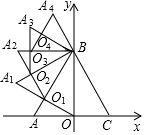
三、解答题
-
23. 如图,已知 是锐角三角形 .
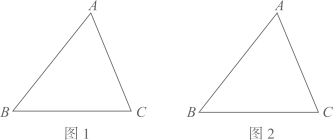 (1)、请在图1中用无刻度的直尺和圆规作图;作直线l,使l上的各点到B、C两点的距离相等;设直线 与 、 分别交于点M、N,作一个圆,使得圆心O在线段 上,且与边 、 相切;(不写作法,保留作图痕迹)(2)、在(1)的条件下,若 , ,则 的半径为.24. 某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图.
(1)、请在图1中用无刻度的直尺和圆规作图;作直线l,使l上的各点到B、C两点的距离相等;设直线 与 、 分别交于点M、N,作一个圆,使得圆心O在线段 上,且与边 、 相切;(不写作法,保留作图痕迹)(2)、在(1)的条件下,若 , ,则 的半径为.24. 某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图.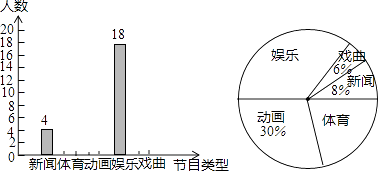
请你根据以上的信息,回答下列问题:
(1)、本次共调查了名学生,其中最喜爱戏曲的有人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是 .(2)、根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.25. 如图, 在平面直角坐标系中,顶点的坐标分别为 , , . (1)、画出与 关于y轴对称的 ;(2)、将 绕点 顺时针旋转90°得到 , 弧是点A所经过的路径,则旋转中心 的坐标为.(3)、求图中阴影部分的面积(结果保留 ).26. 如图,在 中, 的平分线交 于点D,点O在 上,以 为半径的 经过点D,与 交于点E.
(1)、画出与 关于y轴对称的 ;(2)、将 绕点 顺时针旋转90°得到 , 弧是点A所经过的路径,则旋转中心 的坐标为.(3)、求图中阴影部分的面积(结果保留 ).26. 如图,在 中, 的平分线交 于点D,点O在 上,以 为半径的 经过点D,与 交于点E.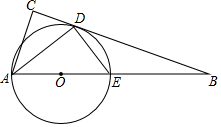 (1)、求证: ;(2)、若 ,求 .27. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 ,与x轴交于A,与y轴交于C,且 .
(1)、求证: ;(2)、若 ,求 .27. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 ,与x轴交于A,与y轴交于C,且 .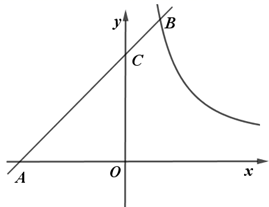 (1)、求一次函数与反比例函数的解析式;(2)、直接写出不等式: 的解集;(3)、P是y轴上一动点,直接写出 叫的最大值和此时点P的坐标.28. 如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.
(1)、求一次函数与反比例函数的解析式;(2)、直接写出不等式: 的解集;(3)、P是y轴上一动点,直接写出 叫的最大值和此时点P的坐标.28. 如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.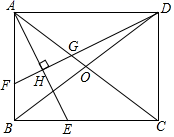 (1)、判断△AFG的形状并说明理由.(2)、求证: .(3)、记△DGO的面积为S1 , △DBF的面积为S2 , 当 时,求 的值.29. 在平面直角坐标系中,抛物线 的最高点为点 ,将 左移1个单位,上移1个单位得到拋物线 ,点P为 的顶点.
(1)、判断△AFG的形状并说明理由.(2)、求证: .(3)、记△DGO的面积为S1 , △DBF的面积为S2 , 当 时,求 的值.29. 在平面直角坐标系中,抛物线 的最高点为点 ,将 左移1个单位,上移1个单位得到拋物线 ,点P为 的顶点.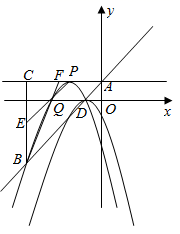 (1)、求抛物线C的解析式;(2)、若过点D的直线l与抛物线 只有一个交点,求直线l的解析式;(3)、直线 与抛物线 交于D、B两点,交y轴于点A,连接 ,过点B作 于点C,点Q为 上 之间的一个动点,连接 交 于点E,连接 并延长交 于点F,试说明: 为定值.
(1)、求抛物线C的解析式;(2)、若过点D的直线l与抛物线 只有一个交点,求直线l的解析式;(3)、直线 与抛物线 交于D、B两点,交y轴于点A,连接 ,过点B作 于点C,点Q为 上 之间的一个动点,连接 交 于点E,连接 并延长交 于点F,试说明: 为定值.