河北省保定市顺平县2021年中考数学二模试卷

试卷更新日期：2021-05-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 在Rt△ABC中，∠C=90°，则∠A是∠B的（）

A、同位角 B、对顶角 C、余角 D、补角

查看试题解析
2. 三根等高的木杆竖直立在平地上，其俯视图如图所示，在某一时刻三根木杆在太阳光下的影子合理的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，直线AB ， CD相交于点O ， OE平分∠AOC ，若∠BOD=70°，则∠DOE的度数是（）

A、70° B、35° C、120° D、145°

查看试题解析
4. 如图，各式从左到右的变形中，是因式分解的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，在网格图中，以D为位似中心，把ΔABC放大到原米的2倍，则点A的对应点为（）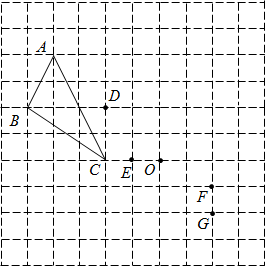

A、O点 B、E点 C、G点 D、F点

查看试题解析
6. 已知，点 $A (2 ， y_{1})$ 、 $B (m ， y_{2})$ 是反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上的两点，且 $y_{1} < y_{2}$ ．满足条件的m值可以是（）

A、-6 B、-1 C、1 D、3

查看试题解析
7. 某地森林火灾受害率控制在0.5‰以下．其中数据0.5‰用科学记数法表示为（）

A、5×10^－3 B、5×10^－4 C、5×10^－5 D、0.5×10^－3

查看试题解析
8. 为了提升学习兴趣，数学老师采用小组竞赛的方法学习分式，要求每小组的四个同学合作完成一道分式计算题，每人只能在前一人的基础上进行一步计算，再将结果传递给下一人，最后完成计算，每做对一步得10分，从哪一步出错，后面的步骤无论对错，全部不计分．某小组计算过程如下所示，该组最终得分为（）
$\frac{x - 3}{x^{2} - 1} + \frac{1}{1 - x}$

$= \frac{x - 3}{(x - 1) (x + 1)} - \frac{1}{(x - 1)}$ ………………甲

$= \frac{x - 3}{(x - 1) (x + 1)} - \frac{x + 1}{(x - 1) (x + 1)}$ ………乙

$= x - 3 - (x + 1)$ ………………………丙

=—2……………………………………丁

A、10分 B、20分 C、30分 D、40分

查看试题解析
9. 在学习菱形时，几名同学对同一问题，给出了如下几种解题思路，其中正确的是（）
已知：如图，四边形ABCD是菱形，E、F是直线AC上两点，AF=CE ．

求证；四边形FBED是菱形．

甲：利用全等，证明四边形FBED四条边相等，进而说明该四边形是菱形；

乙：连接BD ，利用对角线互相垂直的平行四边形是菱形，判定四边形FBED是菱形；

丙：该题目错误，根据已知条件不能够证明该四边形是菱形．

A、甲、乙对，丙错 B、乙、丙对，甲错 C、三个人都对 D、甲、丙对，乙错

查看试题解析
10. 用尺规作已知∠ABC的角平分线，步骤如下：①以B为圆心，以m为半径画弧，分别交射线BA ， BC于点D ， E；②分别以D ， E为圆心，以n为半径画弧，两弧在∠ABC内部交于点P；③画射线BP ，射线BP即为所求．对m ， n的描述，正确的是（）

A、m>0，n>0 B、m>0，n<m； C、m>0，n< $\frac{1}{2}$ DE D、m>0，n> $\frac{1}{2}$ DE

查看试题解析
11. 如图，每个小三角形都是边长为1的正三角形，D、E、F、G四点中有一点是ΔABC的外心，该点到线段AB的距离是（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\sqrt{2}$ C、 $\frac{1}{2}$ D、1

查看试题解析
12. 瓜达尔港是我国实施“一带一路”战略构想的重要一步，为了增进中巴友谊，促进全球经济一体化发展，我国施工队预计把距离港口420km的普通公路升级成同等长度的高速公路，升级后汽车行驶的平均速度比原来提高50％，行驶时间缩短2h，那么汽车原来的平均速度为（）

A、80km/h B、75km/h C、70km/h D、65km/h

查看试题解析
13. 如果一组数据a₁ ， a₂ ， …，a_n的方差是2，那么数据2a₁－2，2a₂－2，…，2a_n－2的方差是（）

A、2 B、4 C、8 D、16

查看试题解析
14. 定义；如果一元二次力程 $a x^{2} + b x + c = 0$ (a≠0)满足a+b+c=0，那么我们称这个方程为“蜻蜓”方程．已知关于x的方程 $a x^{2} + b x + c = 0$ (a≠0)是“蜻蜓”方程，且有两个相等的实数根，则下列结论中正确的是（）

A、a=c≠b B、a=b≠c C、b=c≠a D、a=b=c

查看试题解析
15. 如图，在矩形内画了一些直线，已知△ADH ， △BEF ，四边形HGFC的面积分别是12、32、96，那么图中阴影部分的面积是（）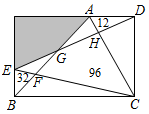

A、48 B、52 C、60 D、108

查看试题解析
16. 如图，已知点A(－1，0)和点B(1，2)，在坐标轴上确定点P，使得△ABP为直角三角形，那么满足条件的点P共有（）

A、2个 B、4个 C、6个 D、7个

查看试题解析

二、填空题

17. 如图所示，一机器人在平地上按图中的步骤行走，要使机器人行走路程不小于10m，则 $α$ 的最大值为．

查看试题解析
18. 如果一个两位数a的个位数字与十位数字都不是零，且互不相同，我们称这个两位数为“跟斗数”，定义新运算：将一个“跟斗数”的个位数字与十位数字对调，把这个新两位数与原两位数的和与11的商记 $ω (a)$ ，例如：a=13，对调个位数字与十位数字得到新两位数31，新两位数与原两位数的和，31+13=44，和与11的商44÷11=4，所以 $ω (13) = 4$ ．根据以上定义，回答下列问题：

(1)、计算： $ω (23) =$ ．

(2)、若一个“跟斗数”b的十位数字是k ，个位数字是2(k+1)，且 $ω (b) = 8$ ，则“跟斗数”b= ．

(3)、若m ， n都是“跟斗数”，且m+n=100，则 $ω (m) + ω (n) =$ ．

查看试题解析

三、解答题

19. 在学习有理数时时我们清楚， $| 3 - (- 1) |$ 表示3与－1的差的绝对值，实际上也可以理解为3与－1两数在数轴上所对应的两点之间的距离；同理|x一5|也可以理解为x与5两数在数轴上所对应的两点之间的距离，试探索并完成以下题目．

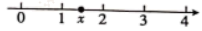(1)、分别计算 $| 8 - (- 3) |$ ， $| - 3 - 5 |$ 的值．

(2)、如图，x是1到2之间的数(包括1，2)，求 $| x - 1 | + | x - 2 | + | x - 3 |$ 的最大值．

查看试题解析

20. 某高中学校为掌握学生的学习情况，优化选科组合，特组织了文化测试，规定：每名学生测试四科，其中A、B ， C为必测学科，第四科D、E中随机抽取．

(1)、据统计，九（1）班有8名同学抽到了D“物理”学科，他们的成绩如下：7，6，8，9，10，5，8，7．

①这组成绩的中位数是，平均数是；

②该班同学丙因病错过了测试，补测抽到了D“物理”学科，加上丙同学的成绩后，发现这9名同学的成绩的众数与中位数相等，但平均数比①中的平均数大，则丙同学“物理”学科的成绩为．

(2)、九（1）班有50名学生，下表是单科成绩统计，请计算出该班此次文化测试的平均成绩．

项目

语文

数学

英语

物理

历史

测试人数(人)

单科平均成绩(分)

(3)、请用列表法或画树状图法，求嘉嘉和琪琪两同学测试的四个学科不完全相同的概率．

查看试题解析

21. 探究：如图1，在Rt△ABC中，∠C=90°，三个内角A、B、C所对的边长分别是a ， b、c ，由于sinA= $\frac{a}{c}$ ，sinB= $\frac{b}{c}$ (已知sin90°=1)．可以但到 $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$ ，即在直角三角形中，每条边和它所对角的正弦值的比值相等．

(1)、拓展：如图2所示，在锐角三角形ABC中，三个内角A、B、C所对的边分别是a ， b、c ， AD⊥BC ， BH⊥AC ，试说明在锐角三角形中也有相同的结论．

(2)、运用：请你运用拓展中的结论，完成下题．如图3，在某海域一货轮在C处测得灯塔A在货轮的北偏西30°的方向上，随后货轮以60海里/小时的速度按北偏东32°的方向航行，半小时后到达B处，此时又测得灯塔A在货轮的北偏西76°的方向上，求此时货轮距灯塔A的距离AB．(计算结果保留一位小数)(参考数据：sin46°≈0.72，sin32°≈0.53，sin62°≈0.88，sin76°≈0.97)

查看试题解析
22. 在矩形ABCD中，AB=6，AD=8，E是边BC上一点(可与B、C重合)，以点E为直角顶点，在AE的右侧作等腰直角△AEF ．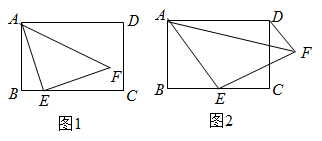

(1)、如图1，当BE的长满足什么条件时，点F在矩形ABCD内？

(2)、如图2，点F在矩形外，连接DF ，若AE∥DF ，求BE的长．

查看试题解析
23. 如图，B、D为线段AH上两点，△ABC、△BDE和△DGH都是等边三角形，连接CE并延长交AH的延长线于点F ，点G恰好在CF上，△ABC的外接圆⊙O交CF于点M ．

(1)、求证：AC²=CM·CF ．

(2)、设等边△ABC、△BDE和△DGH的面积分别为S₁ ， S₂ ， S₃ ．试判断S₁ ， S₂ ， S₃之间的数量关系，并说明理由．

查看试题解析
24. 如图，某小区有块长为(2a+b)米，宽为(2a－b)米的长方形地块，角上有4个边长为(a一b)米的小正方形空地，开发商计划将阴影部分绿化，绿化的总面积为S ，其中a>b ．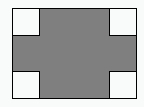

(1)、用含有a和b的式子表示S：． (结果用最简形式表示)

(2)、若a+b=20且 $3^{3 b - a}$ =1，求S的值．

(3)、若a+b=20，则当a ， b为何值时，S有最大值，并求出S的最大值．

查看试题解析
25. 当抛物线 $y = a x^{2} + b x + c$ (a、b、c为常数，c≠0)与x轴交于A ， B两点时，以AB为边作矩形ABCD ，使点C、点D落在直线y=c上，我们把这样的矩形ABCD叫做该抛物线的“相约矩形”．

(1)、①抛物线 $y = x^{2} - 2 x - 3$ 的“相约矩形”的周长为．
②当抛物线 $y = x^{2} - 2 x + c$ (c为常数)不存在“相约矩形”，则c的取值范围是．

(2)、已知抛物线 $y = a x^{2} + b x + 3$ 经过点(2，0)，当该抛物线的“相约矩形”是正方形时，求出该抛物线所对应的函数表达式．

(3)、对于函数 $y = a x^{2} - 2 x + 2 a$ (a为常数)．
①当该函数的图象与x轴只有－个交点时，求出交点的坐标；

②我们把平面直角坐标系中横、纵坐标都为整数的点称为“好点”，当抛物线 $y = a x^{2} - 2 x + 2 a$ (a为常数，a>0)的“相约矩形”内部(包括矩形边界)恰有8个“好点”时，直接写出a的取值范围．

查看试题解析