广东省广州市白云区2021年中考数学一模试卷
试卷更新日期:2021-05-28 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、3 D、2. 在平面直角坐标系中,把点 向左平移2个单位长度,得到点B,点B的坐标为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 如图所示的三棱柱,其俯视图的内角和为( )
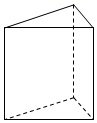 A、 B、 C、 D、5. 如图,在 中, , , , 是 上一点, , ,垂足为E,则 ( )
A、 B、 C、 D、5. 如图,在 中, , , , 是 上一点, , ,垂足为E,则 ( ) A、2 B、3 C、4 D、56. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如图所示,则这些运动员成绩的中位数为( )
A、2 B、3 C、4 D、56. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如图所示,则这些运动员成绩的中位数为( ) A、160 B、165 C、170 D、1757. 如图摆放一副三角尺, ,点E在 上,点D在 的延长线上, , , ,则 ( )
A、160 B、165 C、170 D、1757. 如图摆放一副三角尺, ,点E在 上,点D在 的延长线上, , , ,则 ( )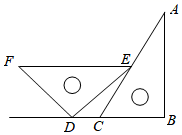 A、 B、 C、 D、8. 关于x的方程 (a为常数)无实数根,则点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 菱形 的对角线 , 相交于点O,且 , ,则四边形 是( )A、梯形 B、矩形 C、菱形 D、正方形10. 设函数 , ,当 时,函数 的最大值是a,函数 的最小值是 ,则 ( )A、4 B、6 C、8 D、10
A、 B、 C、 D、8. 关于x的方程 (a为常数)无实数根,则点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 菱形 的对角线 , 相交于点O,且 , ,则四边形 是( )A、梯形 B、矩形 C、菱形 D、正方形10. 设函数 , ,当 时,函数 的最大值是a,函数 的最小值是 ,则 ( )A、4 B、6 C、8 D、10二、填空题
-
11. 化简 .12. 分解因式: =13. 方程组 的解是 .14. 如图,把一张长方形的纸片对折两次,量出 , ,然后沿 剪下一个 ,展开后得到一个四边形,则这个四边形的周长为 .
 15. 如图,从一块直径为6的圆形铁皮上裁出一个圆心角为 的扇形,把这个扇形围成一个圆锥,则这个圆锥的底面半径是 .
15. 如图,从一块直径为6的圆形铁皮上裁出一个圆心角为 的扇形,把这个扇形围成一个圆锥,则这个圆锥的底面半径是 .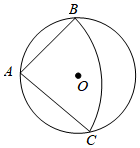 16. 如图,在平面直角坐标系中,有一个 , , ,直角边 在y轴正半轴上,点A在第一象限,且 ,将 绕原点O逆时针旋转 ,同时把各边长扩大为原来的2倍(即 ),得到 ,同理,将 绕原点O逆时针旋转 ,同时把各边长扩大为原来的2倍,得到 ,…,依此规律,得到 ,则点 的纵坐标为 .
16. 如图,在平面直角坐标系中,有一个 , , ,直角边 在y轴正半轴上,点A在第一象限,且 ,将 绕原点O逆时针旋转 ,同时把各边长扩大为原来的2倍(即 ),得到 ,同理,将 绕原点O逆时针旋转 ,同时把各边长扩大为原来的2倍,得到 ,…,依此规律,得到 ,则点 的纵坐标为 .
三、解答题
-
17. 解不等式组: ,并将其解集在数轴上表示出来.18. 如图,已知 平分 , .求证: .
 19. 已知 .(1)、化简M;(2)、x是面积为5的正方形边长,求M的值.20. 某电影院按电影播放的时间段,把某部电影的票价设置为两种,记这两种票价对应的电影票分别为A票和B票.已知每张A票的票价比B票的票价少9元,且用312元购买A票的张数与用420元购买B票的张数相等.求每张A票和B票的票价各是多少元?21. 为落实白云区“数学提升工程”,提升学生数学核心素养,某校开展数学活动周,包括以下项目:①数学知识竞赛;②数学谜语;③数学手抄报;④数学计算接力赛;⑤数独游戏.为了解学生最喜爱的项目,随机抽取若干名学生进行调查,将调查结果绘制成两个不完整的统计图,如图:
19. 已知 .(1)、化简M;(2)、x是面积为5的正方形边长,求M的值.20. 某电影院按电影播放的时间段,把某部电影的票价设置为两种,记这两种票价对应的电影票分别为A票和B票.已知每张A票的票价比B票的票价少9元,且用312元购买A票的张数与用420元购买B票的张数相等.求每张A票和B票的票价各是多少元?21. 为落实白云区“数学提升工程”,提升学生数学核心素养,某校开展数学活动周,包括以下项目:①数学知识竞赛;②数学谜语;③数学手抄报;④数学计算接力赛;⑤数独游戏.为了解学生最喜爱的项目,随机抽取若干名学生进行调查,将调查结果绘制成两个不完整的统计图,如图: (1)、本次随机抽查的学生人数为人,补全图(Ⅰ);(2)、该校共有800名学生,可估计出该校学生最喜爱“①数学知识竞赛”的人数为人,图(Ⅱ)中扇形①的圆心角度数为度;(3)、该校计划在“①,②,③,④”四项活动中随机选取两项参加区活动展示,请用列表或画树状图的方法,求恰好选中“①,④”这两项活动的概率.22. 一次函数 与反比例函数 的图象都经过点 .(1)、求b的值;(2)、点 , , , ,都在反比例函数图象上,根据图象比较 , , 的大小.23. 如图, 是四边形 的外接圆, 是 的直径, ,交 的延长线于点E, 平分 .
(1)、本次随机抽查的学生人数为人,补全图(Ⅰ);(2)、该校共有800名学生,可估计出该校学生最喜爱“①数学知识竞赛”的人数为人,图(Ⅱ)中扇形①的圆心角度数为度;(3)、该校计划在“①,②,③,④”四项活动中随机选取两项参加区活动展示,请用列表或画树状图的方法,求恰好选中“①,④”这两项活动的概率.22. 一次函数 与反比例函数 的图象都经过点 .(1)、求b的值;(2)、点 , , , ,都在反比例函数图象上,根据图象比较 , , 的大小.23. 如图, 是四边形 的外接圆, 是 的直径, ,交 的延长线于点E, 平分 . (1)、求证: 是 的切线.(2)、若 , ,求点B到 的距离.24. 抛物线G: (a为常数)的顶点为A.(1)、用a表示点A的坐标;(2)、经过探究发现,随着a的变化,点A始终在某一抛物线H上,若将抛物线G向右平移 个单位后,所得抛物线顶点B仍在抛物线H上;
(1)、求证: 是 的切线.(2)、若 , ,求点B到 的距离.24. 抛物线G: (a为常数)的顶点为A.(1)、用a表示点A的坐标;(2)、经过探究发现,随着a的变化,点A始终在某一抛物线H上,若将抛物线G向右平移 个单位后,所得抛物线顶点B仍在抛物线H上;①平移距离t是a的函数吗?如果是,求出函数解析式,并写出a的取值范围;如果不是,请说明理由;
②若 在 时,都有y随x的增大而增大,设抛物线H的顶点为C,借助图象,求直线 与x轴交点的横坐标的最小值.
25. 不在射线 上的点P是边长为2的正方形 外一点,且满足 ,以 , 为邻边作 . (1)、如图,若点P在射线 上,请用尺规补全图形;(2)、若点P不在射线 上,且在AB的左侧,求 的度数;(3)、设 与 交点为O,当 的面积最大时,求 的值.
(1)、如图,若点P在射线 上,请用尺规补全图形;(2)、若点P不在射线 上,且在AB的左侧,求 的度数;(3)、设 与 交点为O,当 的面积最大时,求 的值.