广东省佛山市南海区里水镇2021年中考数学模拟试卷
试卷更新日期:2021-05-28 类型:中考模拟
一、单选题
-
1. ﹣2的绝对值是( )A、2 B、 C、 D、2. 下面图形中,是轴对称的是( )A、
 B、
B、 C、
C、 D、
D、 3. 武汉蔡甸火神山医院,是参照抗击非典期间北京小汤山医院模式,在武汉职工疗养院建设一座专门医院,集中收治“新冠状病毒”肺炎患者.医院建筑面积25000平方米,25000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 某小组5名同学在一周内参加体育锻炼的时间如下表所示,关于“锻炼时间”的这组数据,以下说法正确的是( )
3. 武汉蔡甸火神山医院,是参照抗击非典期间北京小汤山医院模式,在武汉职工疗养院建设一座专门医院,集中收治“新冠状病毒”肺炎患者.医院建筑面积25000平方米,25000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 某小组5名同学在一周内参加体育锻炼的时间如下表所示,关于“锻炼时间”的这组数据,以下说法正确的是( )锻炼时间(小时)
2
3
4
5
人数(人)
1
1
2
1
A、中位数是4,平均数是3.5 B、众数是4,平均数是3.5 C、中位数是4,众数是4 D、众数是5,平均数是3.66. 若关于x的一元二次方程x2+2x+k=0有两个不相等的实数根,则k的取值范围是( )A、k<1 B、k>1 C、k=1 D、k≥07. 如图,将一个含有 角的直角三角板的直角顶点放在一张宽为 的矩形纸带边沿上,另一个顶点在纸带的另一边沿上,若测得三角板的一边与纸带的一边所在的直线成 角,则三角板最长的长是( )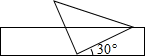 A、 B、 C、 D、8. 如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD的度数为( )
A、 B、 C、 D、8. 如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD的度数为( )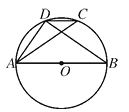 A、 B、 C、 D、9. 不等式组 的解集是( )A、 B、 C、 D、10. 如图, 中, , , .点P是斜边AB上一个动点.过点P作 , 垂足为P, 交边 (或边 ) 于点Q, 设 , 的面积为y,则y与x之间的函数图象大致为( )
A、 B、 C、 D、9. 不等式组 的解集是( )A、 B、 C、 D、10. 如图, 中, , , .点P是斜边AB上一个动点.过点P作 , 垂足为P, 交边 (或边 ) 于点Q, 设 , 的面积为y,则y与x之间的函数图象大致为( )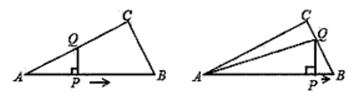 A、
A、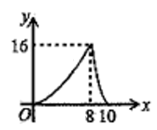 B、
B、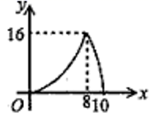 C、
C、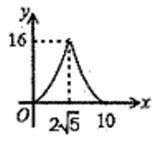 D、
D、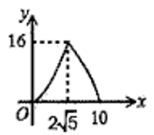
二、填空题
-
11. = .12. 分解因式: .13. 已知正n边形的一个外角是45°,则n=14. 若代数式 有意义,则x的取值范围是 .15. 已知一次函数 的图象上有两点, , ,且 ,则 与 的大小关系是 .16. 如图, 中, , , ,以点B为圆心,以BC长度为半径作弧,交BA于点D , 以点C为圆心,以大于 为半径作弧,接着再以点D为圆心,以相同长度为半径作弧,两弧交于点E , 作射线BE交CA于点F , 以点B为圆心,以BF为长度作弧,交BA于点G , 则阴影部分的面积为 .
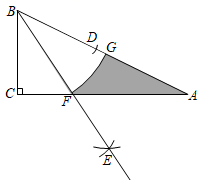 17. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是 .
17. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是 .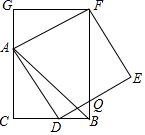
三、解答题
-
18. 计算: .19. 先化简,再求值: ÷(1+ ),其中x= +1.20. “校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
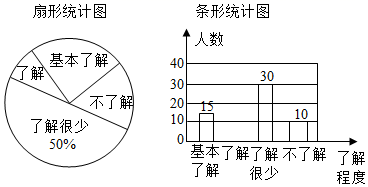 (1)、接受问卷调查的学生共有人,扇形统计图中“了解”部分所对应的扇形的圆心角的度数为 ;(2)、若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为多少人?21. 已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)、接受问卷调查的学生共有人,扇形统计图中“了解”部分所对应的扇形的圆心角的度数为 ;(2)、若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为多少人?21. 已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.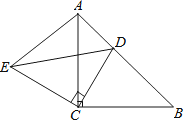 (1)、求证:△ACE≌△BCD;(2)、求证:2CD2=AD2+DB2 .22. 如图,AD是 的直径,PA与 相切于点A , 连接OP , 过点A作 ,垂足为C , 交 于点B , 连接PB并延长交AD的延长线于点E , 连接BD.
(1)、求证:△ACE≌△BCD;(2)、求证:2CD2=AD2+DB2 .22. 如图,AD是 的直径,PA与 相切于点A , 连接OP , 过点A作 ,垂足为C , 交 于点B , 连接PB并延长交AD的延长线于点E , 连接BD.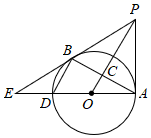 (1)、求证:PB是 的切线;(2)、若 , ,求 .23. 为抗击新型冠状病毒肺炎,某市医院打算采购A、B两种医疗器械,购买1台A机器比购买1台B机器多花10万元,并且花费300万元购买A器材和花费100万元购买B器材的数量相等.(1)、求购买一台A器材和一台B器材各需多少万元;(2)、医院准备购买购A、B两种器材共80台,若购买A、B器材的总费用不高于1050万元,那么最多购买A器材多少台?24. 如图,点A是反比例函数y= (m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
(1)、求证:PB是 的切线;(2)、若 , ,求 .23. 为抗击新型冠状病毒肺炎,某市医院打算采购A、B两种医疗器械,购买1台A机器比购买1台B机器多花10万元,并且花费300万元购买A器材和花费100万元购买B器材的数量相等.(1)、求购买一台A器材和一台B器材各需多少万元;(2)、医院准备购买购A、B两种器材共80台,若购买A、B器材的总费用不高于1050万元,那么最多购买A器材多少台?24. 如图,点A是反比例函数y= (m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图象及y轴分别交于B、
D两点.顺次连接A、B、C、D.设点A的横坐标为n.
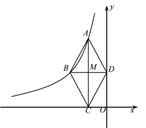 (1)、求点B的坐标(用含有m、n的代数式表示);(2)、求证:四边形ABCD是菱形;(3)、若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.25. 如图,二次函数图象的顶点为坐标系原点O , 且经过点 ,一次函数的图象经过点A和点 .
(1)、求点B的坐标(用含有m、n的代数式表示);(2)、求证:四边形ABCD是菱形;(3)、若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.25. 如图,二次函数图象的顶点为坐标系原点O , 且经过点 ,一次函数的图象经过点A和点 .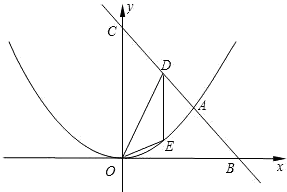 (1)、求二次函数与一次函数的解析式;(2)、如果一次函数图象与y轴相交于点C , 点D在线段AC上,与y轴平行的直线DE与二次函数图象相交于点E , ,求点D的坐标;(3)、当点D在直线AC上的一个动点时,以点O、C、D、E为顶点的四边形能成为平行四边形吗?请说明理由.
(1)、求二次函数与一次函数的解析式;(2)、如果一次函数图象与y轴相交于点C , 点D在线段AC上,与y轴平行的直线DE与二次函数图象相交于点E , ,求点D的坐标;(3)、当点D在直线AC上的一个动点时,以点O、C、D、E为顶点的四边形能成为平行四边形吗?请说明理由.