安徽省滁州市定远县2021年中考数学一模试卷
试卷更新日期:2021-05-28 类型:中考模拟
一、单选题
-
1. 四个实数0、 、 、2中,最小的数是A、0 B、 C、 D、22. 下列计算正确的是( )A、(a+b)2=a2+b2 B、a2+2a2=3a4 C、x2y x2(y≠0) D、(﹣2x2)3=﹣8x63. 如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )
 A、主视图 B、左视图 C、俯视图 D、主视图和左视图4. 全国脱贫攻坚总结表彰大会于2021年2月25日上午在北京人民大会堂隆重举行.我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫.数据“9899万”用科学记数法表示为( )A、9.899×103 B、9.899×107 C、0.9899×108 D、9899×1045. 关于x的方程(x﹣1)(x+2)=m2(m为常数)的根的情况,下列结论中正确的是( )A、两个不相等实数根 B、两个相等实数根 C、没有实数根 D、无法判断根的情况6. 某射击俱乐部将11名成员在某次射击训练中取得的成绩制成如图所示的条形统计图,由图可知,11名成员射击成绩的众数和中位数分别是( )
A、主视图 B、左视图 C、俯视图 D、主视图和左视图4. 全国脱贫攻坚总结表彰大会于2021年2月25日上午在北京人民大会堂隆重举行.我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫.数据“9899万”用科学记数法表示为( )A、9.899×103 B、9.899×107 C、0.9899×108 D、9899×1045. 关于x的方程(x﹣1)(x+2)=m2(m为常数)的根的情况,下列结论中正确的是( )A、两个不相等实数根 B、两个相等实数根 C、没有实数根 D、无法判断根的情况6. 某射击俱乐部将11名成员在某次射击训练中取得的成绩制成如图所示的条形统计图,由图可知,11名成员射击成绩的众数和中位数分别是( ) A、8,9 B、8,8 C、8,10 D、9,87. 已知直线 经过第一、二、三象限,且点 在该直线上,设 ,则m的取值范围是( )A、 B、 C、 D、8. 如图,在△ABC中,BC=16,点D是△ABC内的一点,BD平分∠ABC , 且DB=DC=10,连接AD , ∠ADB=90°,则AD的长是( )
A、8,9 B、8,8 C、8,10 D、9,87. 已知直线 经过第一、二、三象限,且点 在该直线上,设 ,则m的取值范围是( )A、 B、 C、 D、8. 如图,在△ABC中,BC=16,点D是△ABC内的一点,BD平分∠ABC , 且DB=DC=10,连接AD , ∠ADB=90°,则AD的长是( ) A、6 B、7 C、8 D、9. 如图,AB是⊙O的直径,点E是AB上一点,过点E作CD⊥AB , 交⊙O于点C , D , 以下结论正确的是( )
A、6 B、7 C、8 D、9. 如图,AB是⊙O的直径,点E是AB上一点,过点E作CD⊥AB , 交⊙O于点C , D , 以下结论正确的是( ) A、若⊙O的半径是2,点E是OB的中点,则CD= B、若CD= ,则⊙O的半径是1 C、若∠CAB=30°,则四边形OCBD是菱形 D、若四边形OCBD是平行四边形,则∠CAB=60°10. 已知一次函数 与反比例函数 的图象在第二象限有两个交点,且其中一个交点的横坐标为 ,则二次函数 的图象可能是( )A、
A、若⊙O的半径是2,点E是OB的中点,则CD= B、若CD= ,则⊙O的半径是1 C、若∠CAB=30°,则四边形OCBD是菱形 D、若四边形OCBD是平行四边形,则∠CAB=60°10. 已知一次函数 与反比例函数 的图象在第二象限有两个交点,且其中一个交点的横坐标为 ,则二次函数 的图象可能是( )A、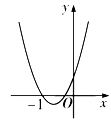 B、
B、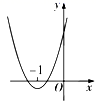 C、
C、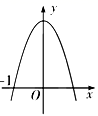 D、
D、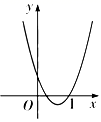
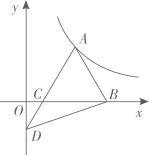
二、填空题
-
11. 计算: .12. 分解因式:ab2﹣2ab+a= .13. 如图,在 中, ,点A在反比例函数 ( , )的图象上,点B,C在x轴上, ,延长 交y轴于点D,连接 ,若 的面积等于1,则k的值为.
 14. 将矩形ABCD按如图方式折叠:BE , EG , FG为折痕,若顶点A , C , D都落在点O处,且点B , O , G在同一直线上,同时点E , O , F在另一条直线上.请完成下列探究:
14. 将矩形ABCD按如图方式折叠:BE , EG , FG为折痕,若顶点A , C , D都落在点O处,且点B , O , G在同一直线上,同时点E , O , F在另一条直线上.请完成下列探究: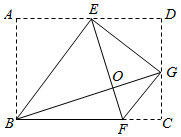 (1)、∠BEG的大小为;(2)、若AD=4,则四边形BEGF的面积为 .
(1)、∠BEG的大小为;(2)、若AD=4,则四边形BEGF的面积为 .三、解答题
-
15. 计算:(π﹣3.14)0+| ﹣2|﹣( ) ﹣2+ cos45°.16. 如图,在平面直角坐标系中,给出了格点△ABC(顶点是网格线的交点),已知点B的坐标为(1,2).
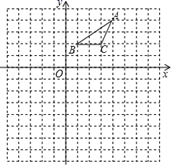
⑴画出△ABC关于y轴对称的△A1B1C1 , 并写出点B1的坐标;
⑵在给定的网格中,以点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2 , 画出△A2B2C2;并写出点B2的坐标.
17. 观察以下等式:第1个等式: ;
第2个等式: ;
第3个等式: ;
第4个等式: ;
第5个等式: ;
…
按照以上规律,解决下列问题:
(1)、写出第6个等式:;(2)、写出你猜想的第n个等式:(用含n的等式表示),并证明.18. 某兴趣小组为了测量大楼 的高度,先沿着斜坡 走了 米到达坡顶点 处,然后在点 处测得大楼顶点 的仰角为 ,已知斜坡 的坡度为 ,点 到大楼的距离 为 米,求大楼的高度 .(参考数据: , , )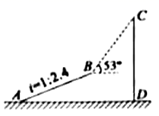 19. 小明家在安徽某市经营了甲,乙两个连锁超市,这两个连锁超市4月份的销售额均为m万元,在5月份和6月份这两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减少x%.(1)、6月份甲超市的销售额比乙超市的销售额多万元(用含m , x的式子表示);(2)、若m=10,且6月份甲超市的销售额比乙超市多0.8万元,求x的值.20. 如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC相交于点M、N.
19. 小明家在安徽某市经营了甲,乙两个连锁超市,这两个连锁超市4月份的销售额均为m万元,在5月份和6月份这两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减少x%.(1)、6月份甲超市的销售额比乙超市的销售额多万元(用含m , x的式子表示);(2)、若m=10,且6月份甲超市的销售额比乙超市多0.8万元,求x的值.20. 如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC相交于点M、N. (1)、过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;(2)、连接MD,求证:MD=NB.21. 戏曲进校园,经典共传承.为进一步弘扬中华优秀传统文化,提高学生的国学素养,某校举行了戏曲文化知识竞赛,将所有参赛选手的成绩(单位:分,均为整数)分成了A(89.5<n≤100),B(79.5<n<89.5),C(69.5<n<79.5),D(59.5<n<69.5)四个等级,根据成绩绘制成如下统计图表(部分信息未给出):
(1)、过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;(2)、连接MD,求证:MD=NB.21. 戏曲进校园,经典共传承.为进一步弘扬中华优秀传统文化,提高学生的国学素养,某校举行了戏曲文化知识竞赛,将所有参赛选手的成绩(单位:分,均为整数)分成了A(89.5<n≤100),B(79.5<n<89.5),C(69.5<n<79.5),D(59.5<n<69.5)四个等级,根据成绩绘制成如下统计图表(部分信息未给出):等级
成绩n/分
频数
A
94.5<n≤100
2
89.5<n<94.5
B
84.5<n<89.5
6
79.5<n<84.5
14
C
74.5<n<79.5
16
69.5<n<74.5
D
64.5<n<69.5
3
59.5<n<64.5
2
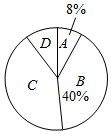 (1)、本次参赛选手共有名,在扇形统计图中,C等级所在扇形的圆心角的度数为;(2)、赛前规定,成绩由高到低前30%的选手获奖,选手小明的成绩为86分,试判断他是否获奖,并说明理由;(3)、学校准备从成绩为A等级的选手中任选2名学生作为代表在全校师生大会上发言,求选中的2名学生至少有1名学生的成绩不低于95分的概率.22. 如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B , 连接OA , 二次函数y=x2图象从点O沿OA方向平移,与直线x=2交于点P , 顶点M到A点时停止移动.
(1)、本次参赛选手共有名,在扇形统计图中,C等级所在扇形的圆心角的度数为;(2)、赛前规定,成绩由高到低前30%的选手获奖,选手小明的成绩为86分,试判断他是否获奖,并说明理由;(3)、学校准备从成绩为A等级的选手中任选2名学生作为代表在全校师生大会上发言,求选中的2名学生至少有1名学生的成绩不低于95分的概率.22. 如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B , 连接OA , 二次函数y=x2图象从点O沿OA方向平移,与直线x=2交于点P , 顶点M到A点时停止移动. (1)、求线段OA所在直线的函数解析式;(2)、二次函数的顶点M与A重合时,函数的图象是否过点Q(a , a﹣1),并说明理由;(3)、设二次函数顶点M的横坐标为m , 当m为何值时,线段PB最短,并求出二次函数的解析式.23.
(1)、求线段OA所在直线的函数解析式;(2)、二次函数的顶点M与A重合时,函数的图象是否过点Q(a , a﹣1),并说明理由;(3)、设二次函数顶点M的横坐标为m , 当m为何值时,线段PB最短,并求出二次函数的解析式.23. (1)、证明推断:如图(1),在正方形ABCD中,点E , Q分别在边BC , AB上,DQ⊥AE于点O , 点G , F分别在边CD , AB上,GF⊥AE .
(1)、证明推断:如图(1),在正方形ABCD中,点E , Q分别在边BC , AB上,DQ⊥AE于点O , 点G , F分别在边CD , AB上,GF⊥AE .①求证:DQ=AE;
②推断: 的值为;
(2)、类比探究:如图(2),在矩形ABCD中, =k(k为常数).将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形FEPG , EP交CD于点H , 连接AE交GF于点O . 试探究GF与AE之间的数量关系,并说明理由;(3)、拓展应用:在(2)的条件下,连接CP , 当k= 时,若tan∠CGP= ,GF=2 ,求CP的长.