安徽省安庆市怀宁县2021年中考数学模拟试卷
试卷更新日期:2021-05-28 类型:中考模拟
一、单选题
-
1. 下列所给图形是中心对称图形但不是轴对称图形的是( )A、
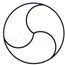 B、
B、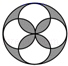 C、
C、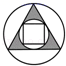 D、
D、 2. 已知 ,则 的值为( )A、﹣3 B、3 C、 D、3. 第七届世界军人运动会将于2019年10月在武汉举行,届时将需要200000名城市志愿者和50000名赛会志愿者.数250000用科学记数法表示为( )A、2.5×104 B、25×104 C、2.5×105 D、0.25×1064. 如果反比例函数y= (a是常数)的图象在第二、四象限,那么a的取值范围是( )A、a>2 B、a<2 C、a>0 D、a<05. 如图所示的几何体的左视图为( )
2. 已知 ,则 的值为( )A、﹣3 B、3 C、 D、3. 第七届世界军人运动会将于2019年10月在武汉举行,届时将需要200000名城市志愿者和50000名赛会志愿者.数250000用科学记数法表示为( )A、2.5×104 B、25×104 C、2.5×105 D、0.25×1064. 如果反比例函数y= (a是常数)的图象在第二、四象限,那么a的取值范围是( )A、a>2 B、a<2 C、a>0 D、a<05. 如图所示的几何体的左视图为( )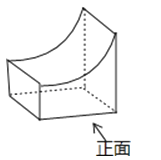 A、
A、 B、
B、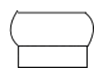 C、
C、 D、
D、 6. 若锐角α满足cosα< 且tanα< ,则α的范围是( )A、30°<α<45° B、45°<α<60° C、60°<α<90° D、30°<α<60°7. 若将半径为10cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为( )A、5cm B、4cm C、3cm D、2cm8. 如图,随机闭合开关S1 , S2 , S3中的两个,灯泡不能够发光的概率是( )
6. 若锐角α满足cosα< 且tanα< ,则α的范围是( )A、30°<α<45° B、45°<α<60° C、60°<α<90° D、30°<α<60°7. 若将半径为10cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为( )A、5cm B、4cm C、3cm D、2cm8. 如图,随机闭合开关S1 , S2 , S3中的两个,灯泡不能够发光的概率是( )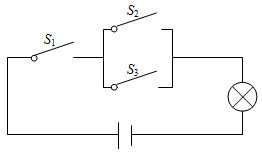 A、 B、 C、 D、9. 如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,点O是AB的三等分点,半圆O与AC相切,M , N分别是BC与半圆弧上的动点,则MN的最大值与最小值之差是( )
A、 B、 C、 D、9. 如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,点O是AB的三等分点,半圆O与AC相切,M , N分别是BC与半圆弧上的动点,则MN的最大值与最小值之差是( ) A、5 B、6 C、7 D、810. 如图,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP′,连接DP′,则DP′的最小值是( )
A、5 B、6 C、7 D、810. 如图,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP′,连接DP′,则DP′的最小值是( )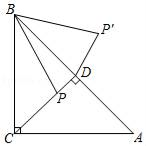 A、2 -2 B、4﹣2 C、2﹣ D、 -1
A、2 -2 B、4﹣2 C、2﹣ D、 -1二、填空题
-
11. 的平方根是 .12. 在平面直角坐标系中,将一块直角三角板如图放置,直角顶点与原点O重合,顶点A , B恰好分别落在函数y=﹣ (x<0),y= (x>0)的图象上,则sin∠BAO的值为 .
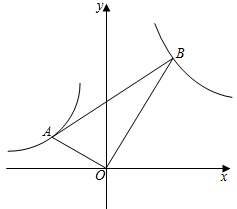 13. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=55°,则∠BCD=°.
13. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=55°,则∠BCD=°.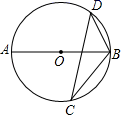 14. 已知函数y=(a﹣1)x2﹣2ax+a﹣3的图象与两坐标轴共有两个交点,则a的值为 .
14. 已知函数y=(a﹣1)x2﹣2ax+a﹣3的图象与两坐标轴共有两个交点,则a的值为 .三、解答题
-
15. ﹣23+(π﹣3)0﹣2﹣1+sin30°.16. 解不等式组 ,并把解集在数轴上表示出来.17. 如图所示,我县某中学课外活动小组的同学利用所学知识去测量怀安河的宽度,小明同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处20米远的B处测得∠CBA=30°,请你根据这些数据算出河宽.(结果保留根号)
 18. 某花店销售甲、乙两种鲜花,销售5束甲种、1束乙种鲜花,可获利润38元;销售6束甲种、3束乙种鲜花,可获利润60元.(1)、问该花店销售甲、乙两种鲜花,每只的利润分别是多少元?(2)、在(1)中,花店共销售甲、乙两种鲜花50束,其中甲种鲜花为a束,求花店所获利p与a的函数关系式.并求当a≥20时p的最大值.19. 如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O , 点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E .
18. 某花店销售甲、乙两种鲜花,销售5束甲种、1束乙种鲜花,可获利润38元;销售6束甲种、3束乙种鲜花,可获利润60元.(1)、问该花店销售甲、乙两种鲜花,每只的利润分别是多少元?(2)、在(1)中,花店共销售甲、乙两种鲜花50束,其中甲种鲜花为a束,求花店所获利p与a的函数关系式.并求当a≥20时p的最大值.19. 如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O , 点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E .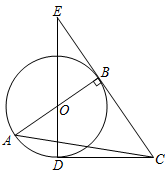 (1)、判断直线CD与⊙O的位置关系,并证明;(2)、若BE=8,DE=16,求⊙O的半径.20. 如图,一次函数y=mx+n(m≠0)的图象与反比例函数y= (k≠0)的图象交于第二、四象限内的点A(a , 6)和点B(18,b).过点A作x轴的垂线,垂足为点C , △AOC的面积为9.
(1)、判断直线CD与⊙O的位置关系,并证明;(2)、若BE=8,DE=16,求⊙O的半径.20. 如图,一次函数y=mx+n(m≠0)的图象与反比例函数y= (k≠0)的图象交于第二、四象限内的点A(a , 6)和点B(18,b).过点A作x轴的垂线,垂足为点C , △AOC的面积为9.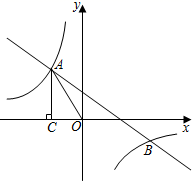 (1)、分别求出a和b的值;(2)、在x轴上取点P , 使PA﹣PB取得最大值时,求出点P的坐标.21. 已知:如图,在△ABC中,AD⊥BC于点D , AE:ED=7:5,连接CE并延长交边AB于点F , AC=13,BC=8,cos∠ACB= .
(1)、分别求出a和b的值;(2)、在x轴上取点P , 使PA﹣PB取得最大值时,求出点P的坐标.21. 已知:如图,在△ABC中,AD⊥BC于点D , AE:ED=7:5,连接CE并延长交边AB于点F , AC=13,BC=8,cos∠ACB= .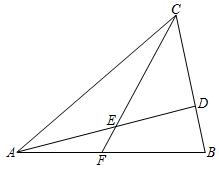 (1)、求tan∠DCE的值;(2)、求 的值.22. 随着智能手机的普及率越来越高以及移动支付的快捷高效性,中国移动支付在世界处于领先水平,为了解人们平时最喜欢用哪种移动支付方式,因此在某步行街对行人进行随机抽样调查,以下是根据调查结果分别整理的不完整的统计表和统计图.
(1)、求tan∠DCE的值;(2)、求 的值.22. 随着智能手机的普及率越来越高以及移动支付的快捷高效性,中国移动支付在世界处于领先水平,为了解人们平时最喜欢用哪种移动支付方式,因此在某步行街对行人进行随机抽样调查,以下是根据调查结果分别整理的不完整的统计表和统计图.移动支付方式
支付宝
微信
其他
人数/人
200
90
请你根据上述统计表和统计图提供的信息.完成下列问题:
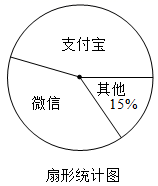 (1)、在此次调查中,使用支付宝支付的人数为人,表示微信支付的扇形所对的圆心角度数为度.(2)、某天该步行街人流量为3万人,其中80%的人购物并选择移动支付,请你依据此次调查获得的信息估计一下当天使用微信支付的人数.(3)、甲、乙、丙三人都只习惯使用支付宝和微信支付,并且他们选择这两种支付的可能性是相同的,请计算三人恰好选择同一种支付方式的概率.23. 如图,在直角坐标平面内,抛物线经过原点O、点B(1,3),又与x轴正半轴相交于点A , ∠BAO=45°,点P是线段AB上的一点,过点P作PM∥OB , 与抛物线交于点M , 且点M在第一象限内.
(1)、在此次调查中,使用支付宝支付的人数为人,表示微信支付的扇形所对的圆心角度数为度.(2)、某天该步行街人流量为3万人,其中80%的人购物并选择移动支付,请你依据此次调查获得的信息估计一下当天使用微信支付的人数.(3)、甲、乙、丙三人都只习惯使用支付宝和微信支付,并且他们选择这两种支付的可能性是相同的,请计算三人恰好选择同一种支付方式的概率.23. 如图,在直角坐标平面内,抛物线经过原点O、点B(1,3),又与x轴正半轴相交于点A , ∠BAO=45°,点P是线段AB上的一点,过点P作PM∥OB , 与抛物线交于点M , 且点M在第一象限内.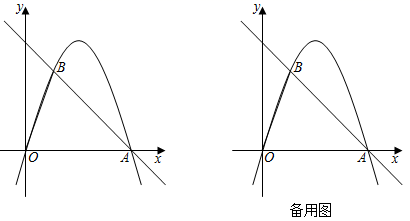 (1)、求直线AB和抛物线的表达式;(2)、连接BM , 若∠BMP=∠AOB ,
(1)、求直线AB和抛物线的表达式;(2)、连接BM , 若∠BMP=∠AOB ,①求证:BM∥OA;
②求点P的坐标;
③请直接写出四边形OBMA的外接圆的圆心坐标.